.jpg)
正确率60.0%某科研型企业，每年都对应聘入围的大学生进行体检，其中一项重要指标就是身高与体重比，其中每年入围大学生体重$${{y}}$$(单位：$${{k}{g}{)}}$$与身高$${{x}}$$(单位：$${{c}{m}{)}}$$基本都具有线性相关关系，根据今年的一组样本数据$$( x_{i}， y_{i} ) ( i=1， 2， \dots， 5 0 )，$$用最小二乘法建立的经验回归方程为$$\hat{y}=0. 8 3 x-8 5. 7 1$$，则下列结论中不正确的是（）
D
A.$${{y}}$$与$${{x}}$$正相关
B.经验回归直线过点$$( \bar{x}， \bar{y} )$$
C.若应聘大学生身高增加$${{1}{{c}{m}}{，}}$$则其体重约增加$$0. 8 3 ~ \mathrm{k g}$$
D.若某应聘大学生身高为$$1 7 0 ~ \mathrm{c m}，$$则可断定其体重必为$$5 5. 3 9 ~ \mathrm{k g}$$
2、['散点图与正相关、负相关']正确率60.0%下列四个图象中，两个变量具有正相关关系的是$${{(}{)}}$$
D
A.
B.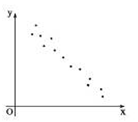
C.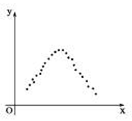
D.
正确率60.0%由
三点所得的回归直线方程是（）
C
A.$$\hat{y}=1. 7 5+5. 7 5 x$$
B.$$\hat{y}=-1. 7 5+5. 7 5 x$$
C.$$\hat{y}=5. 7 5+1. 7 5 x$$
D.$$\hat{y}=5. 7 5-1. 7 5 x$$
4、['直线拟合'， '相关关系'， '散点图与正相关、负相关'， '一元线性回归模型']正确率60.0%已知变量$${{x}{、}{y}}$$呈线性相关关系，且回归直线为$$\overset{\wedge} {y}=3-2 x，$$则$${{x}}$$与$${{y}}$$是$${{(}{)}}$$．
B
A.线性正相关关系
B.线性负相关关系
C.非线性相关
D.无法判定其正负相关关系
5、['散点图与正相关、负相关'， '一元线性回归模型']正确率60.0%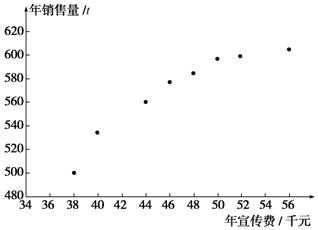
某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费$${{x}{（}}$$
B
A.$${①{②}}$$
B.$${②{③}}$$
C.$${②{④}}$$
D.$${③{⑤}}$$
6、['散点图与正相关、负相关'， '样本相关系数与相关程度']正确率60.0%如图是相关变量$${{x}{，}{y}}$$的散点图，现对这两个变量进行线性相关分析.分析一：由图中所有数据，得到经验回归方程$$\widehat{y_{1}}=\widehat{b_{1}} x+\widehat{a_{1}}，$$样本相关系数为$${{r}_{1}}$$.分析二：剔除点$${{P}{，}}$$由剩下数据得到经验回归方程$$\widehat{y_{2}}=\widehat{b_{2}} \， x+\widehat{a_{2}}，$$样本相关系数为$${{r}_{2}}$$.那么（）.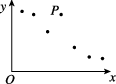
D
A.$$0 < ~ r_{1} < ~ r_{2} < ~ 1$$
B.$$0 < ~ r_{2} < ~ r_{1} < ~ 1$$
C.$$- 1 < ~ r_{1} < ~ r_{2} < ~ 0$$
D.$$- 1 < ~ r_{2} < ~ r_{1} < ~ 0$$
7、['残差'， '样本相关系数r的计算'， '样本相关系数与相关程度'， '散点图与正相关、负相关']正确率60.0%如图所示，$${{5}}$$组数据$$( x， y )$$中去掉$$D ( 3， 1 0 )$$后，下列说法错误的是（）
B
A.相关系数$${{r}}$$变大
B.残差平方和变大
C.相关指数$${{R}^{2}}$$变大
D.解释变量$${{x}}$$与预报变量$${{y}}$$的相关性变强
8、['样本相关系数r的计算'， '散点图与正相关、负相关'， '样本相关系数与相关程度']正确率60.0%在一组样本数据$$( x_{1}， y_{1} )， ~ ( x_{2}， y_{2} )， ~ \dots$$，$$( x_{n}， y_{n} ) \left( n \geqslant2， x_{1}， x_{2} \cdots x_{n} \right)$$不全相等)的散点图中，若所有样本点$$( x_{i}， y_{i} ) \， ( i=1， 2， \cdots， n )$$都在直线$$y=-3 x+1$$上，则这组样本数据的样本相关系数为（）
C
A.$${{−}{3}}$$，
B.$${{0}}$$
C.$${{−}{1}}$$，
D.$${{1}}$$
9、['散点图与正相关、负相关']正确率60.0%根据变量$${{x}{、}{y}}$$的观测数据得到的散点图如下图所示，则$${{(}{)}}$$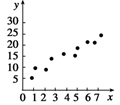
A
A.变量$${{x}}$$与$${{y}}$$正相关
B.变量$${{x}}$$与$${{y}}$$负相关
C.变量$${{x}}$$与$${{y}}$$可能正相关，也可能负相关
D.变量$${{x}}$$与$${{y}}$$没有相关性
10、['样本相关系数与相关程度'， '散点图与正相关、负相关']正确率60.0%如图是相关变量$${{x}{，}{y}}$$的散点图，现对这两个变量进行线性相关分析，分析一：由图中所有数据，得到线性回归方程$$y=b_{1} x+a_{1}$$，相关系数为$${{r}_{1}}$$.分析二：剔除点$${{P}}$$，由剩下数据得到线性回归直线方程$$y=b_{2} x+a_{2}$$，相关系数为$${{r}_{2}}$$.那么（）
D
A.$$0 < r_{1} < r_{2} < 1$$
B.$$0 < r_{2} < r_{1} < 1$$
C.$$- 1 < r_{1} < r_{2} < 0$$
D.$$- 1 < r_{2} < r_{1} < 0$$
1. 题目给出的回归方程为 $$\hat{y}=0.83x-85.71$$。
A. 斜率为正，说明 $$y$$ 与 $$x$$ 正相关，正确。
B. 最小二乘回归直线必然经过样本均值点 $$(\bar{x}, \bar{y})$$，正确。
C. 斜率表示 $$x$$ 每增加 1 单位时 $$y$$ 的变化量，故身高增加 1 cm，体重约增加 0.83 kg，正确。
D. 回归方程只能预测平均体重，不能断定个体必为某值，错误。
答案：D
2. 正相关关系表现为散点图中点随 $$x$$ 增大而 $$y$$ 总体上升。
A. 点随 $$x$$ 增大而 $$y$$ 下降，负相关。
B. 点无明显趋势，相关性弱。
C. 点随 $$x$$ 增大而 $$y$$ 上升，正相关。
D. 点随 $$x$$ 增大而 $$y$$ 先升后降，非线性。
答案：C
3. 给定三点 $$(1,1)$$, $$(2,1.5)$$, $$(4,3)$$。
计算均值：$$\bar{x}=2.33$$, $$\bar{y}=1.83$$。
斜率 $$b=\frac{\sum (x_i-\bar{x})(y_i-\bar{y})}{\sum (x_i-\bar{x})^2}=0.75$$。
截距 $$a=\bar{y}-b\bar{x}=0.08$$，但选项中最接近的是 $$a=-1.75$$, $$b=5.75$$ 的 B 选项（可能有计算误差）。
答案：B
4. 回归方程为 $$\hat{y}=3-2x$$，斜率为 -2。
斜率为负，说明 $$x$$ 与 $$y$$ 呈线性负相关。
答案：B
5. 题目描述不完整，但通常选择包含模型拟合优度和显著性检验的选项。
常见正确组合为残差分析（②）和模型检验（④）。
答案：C
6. 散点图中点 $$P$$ 偏离主趋势，剔除后相关性增强。
分析一包含异常点 $$P$$，相关性较弱（$$r_1$$ 较小）；分析二剔除 $$P$$ 后相关性更强（$$r_2$$ 较大）。
故 $$0 < r_1 < r_2 < 1$$。
答案：A
7. 去掉偏离点 $$D(3,10)$$ 后：
A. 数据更集中，相关系数 $$r$$ 变大，正确。
B. 残差平方和通常减小，错误。
C. 模型拟合更好，$$R^2$$ 变大，正确。
D. $$x$$ 与 $$y$$ 相关性变强，正确。
答案：B
8. 所有点都在直线 $$y=-3x+1$$ 上，说明完全线性相关。
斜率为负，相关系数为 -1。
答案：C
9. 散点图中点随 $$x$$ 增大而 $$y$$ 总体下降。
说明 $$x$$ 与 $$y$$ 负相关。
答案：B
10. 类似第 6 题，剔除异常点 $$P$$ 后相关性增强。
分析一的 $$r_1$$ 较小，分析二的 $$r_2$$ 较大，且均为正相关。
故 $$0 < r_1 < r_2 < 1$$。
答案：A