正确率60.0%某同学寒假期间对其$${{3}{0}}$$位亲属的饮食习惯进行了一次调查,列出了如下$${{2}{×}{2}}$$列联表:
单位:位
| 年龄 | 饮食习惯 | 总计 | |
| 偏爱蔬菜 | 偏爱肉类 | ||
| 50岁及以下 | 4 | 8 | 12 |
| 50岁及以上 | 16 | 2 | 18 |
| 总计 | 20 | 10 | 30 |
则可以认为其亲属的饮食习惯与年龄有关的把握为 ()
附:$$\chi^{2}=\frac{n ( a d-b c )^{2}} {( a+b ) ( c+d ) ( a+c ) ( b+d )},$$其中$$n=a+b+c+d$$.
| $$P ( \chi^{2} > k )$$ | $${{0}{.}{1}}$$ | $${{0}{.}{0}{5}}$$ | $${{0}{.}{0}{1}}$$ |
| $${{k}}$$ | $$2. 7 0 6$$ | $$3. 8 4 1$$ | $$6. 6 3 5$$ |
C
A.$${{9}{0}{%}}$$
B.$${{9}{5}{%}}$$
C.$${{9}{9}{%}}$$
D.不相关
2、['列联表', '独立性检验及其应用']正确率60.0%在一次独立性检验中,得出列联表如下:
| 分类变量 $${{B}}$$ 的情况 | 分类变量 $${{A}}$$ 的情况 | 合计 | |
| $${{M}}$$ | $$\overline{{M}}$$ | ||
| $${{N}}$$ | $${{2}{0}{0}}$$ | $${{8}{0}{0}}$$ | $${{1}{0}{0}{0}}$$ |
| $${{N}^{¯}}$$ | $${{1}{8}{0}}$$ | $${{a}}$$ | $$1 8 0+a$$ |
| 合计 | $${{3}{8}{0}}$$ | $$8 0 0+a$$ | $$1 1 8 0+a$$ |
B
A.$${{2}{0}{0}}$$
B.$${{7}{2}{0}}$$
C.$${{1}{0}{0}}$$
D.$${{1}{8}{0}}$$
3、['列联表', '独立性检验及其应用', '用频率估计概率']正确率60.0%千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在地区$${{1}{0}{0}}$$天的日落情况和半夜后的天气,得到如下$${{2}{×}{2}}$$列联表:
单位:天
| “日落云里走” 是否出现 | 半夜后的天气 | 合计 | |
| 下雨 | 未下雨 | ||
| 出现 | $${{2}{5}}$$ | $${{5}}$$ | $${{3}{0}}$$ |
| 未出现 | $${{2}{5}}$$ | $${{4}{5}}$$ | $${{7}{0}}$$ |
| 合计 | $${{5}{0}}$$ | $${{5}{0}}$$ | $${{1}{0}{0}}$$ |
D
A.估计该地区半夜后下雨的概率为$$\frac{1} {2}$$
B.估计该地区未出现“日落云里走”半夜后下雨的概率为$$\frac{5} {1 4}$$
C.若认为“日落云里走”与“雨在半夜后”有关联,则犯错误的概率不大于$$\ 0. 0 0 1$$
D.若出现“日落云里走”,则半夜后有$$9 9. 9 7_{0}$$的可能性会下雨
4、['列联表']正确率60.0%现在大部分高中学生在高一升高二时仍然面临着选文理科的问题,某校抽取了部分男、女学生选文理科意愿的一份样本,制作出如图所示的两个等高条形图.根据图中的信息,下列结论不正确的是()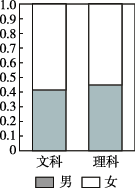 ①
①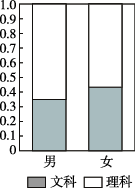 ②
②
D
A.样本中的女生数量多于男生数量
B.样本中有理科意愿的学生数量多于有文科意愿的学生数量
C.样本中的男生偏爱理科
D.样本中的女生偏爱文科
5、['列联表']正确率60.0%根据下面列联表作出的等高堆积条形图中正确的是()
| $${{X}}$$ | $${{Y}}$$ | 合计 | |
| $${{y}_{1}}$$ | $${{y}_{2}}$$ | ||
| $${{x}_{1}}$$ | $${{1}}$$ | $${{5}}$$ | |
| $${{x}_{2}}$$ | $${{2}}$$ | ||
| 合计 | $${{1}{0}}$$ | ||

D
A.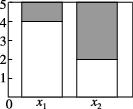
B.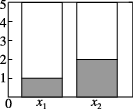
C.
D.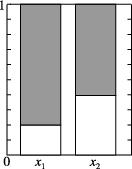
正确率80.0%在等高堆积条形图中,两个因式的比值相差越大,要推断的论述成立的可能性就越大的是()
C
A.$$\frac{a} {a+b}$$与$$\frac{d} {c+b}$$
B.$$\frac{c} {a+b}$$与$$\frac{a} {c+b}$$
C.$$\frac{a} {a+b}$$与$$\frac{c} {c+d}$$
D.$$\frac{a} {a+b}$$与$$\frac{c} {b+c}$$
7、['列联表', '独立性检验及其应用']正确率60.0%根据如表,计算$${{X}^{2}{≈}{(}}$$)
| 又发病 | 未发病 | |
| 做移植手术 | $${{3}{9}}$$ | $${{1}{5}{7}}$$ |
| 未做移植手术 | $${{2}{9}}$$ | $${{1}{6}{7}}$$ |
C
A.$${{1}{.}{5}{1}}$$
B.$${{1}{.}{6}{2}}$$
C.$${{1}{.}{7}{8}}$$
D.$${{1}{.}{7}{5}}$$
8、['列联表', '分层随机抽样的概念']正确率60.0%如图是调查某学校高三年级男女学生是否喜欢篮球运动的等高条形图,阴影部分的高表示喜欢该项运动的频率.已知该年级男生女生各$${{5}{0}{0}}$$名(假设所有学生都参加了调查),现从所有喜欢篮球运动的同学中按分层抽样的方式抽取$${{3}{2}}$$人,则抽取的男生人数为()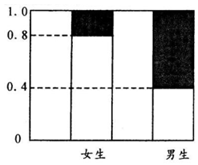
D
A.$${{8}}$$
B.$${{1}{2}}$$
C.$${{1}{6}}$$
D.$${{2}{4}}$$
9、['列联表', '独立性检验及其应用']正确率60.0%为直观判断两个分类变量$${{X}}$$和$${{Y}}$$之间是否有关系,若它们的取值分别为$$\{x_{1}, x_{2} \}$$和$$\{y_{1}, y_{2} \},$$通过抽样得到频数表如图,则下列哪两个比值相差越大,可判断两个分类变量之间的关系应该越强()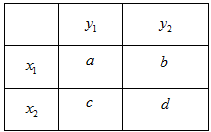
A
A.$$\frac{a} {a+c}$$与$$\frac b {b+d}$$
B.$$\frac{a} {a+d}$$与$$\frac{c} {b+c}$$
C.$$\frac{a} {b+d}$$与$$\frac{c} {a+c}$$
D.$$\frac{a} {c+d}$$与$$\frac{c} {a+b}$$
10、['列联表', '分层随机抽样的概念', '频数与频率']正确率60.0%如图是调查某学校高三年级男女学生是否喜欢数学的等高条形图,阴影部分的高表示喜欢数学的频率.已知该年级男生女生各$${{5}{0}{0}}$$名(所有学生都参加了调查$${{)}}$$,现从所有喜欢数学的同学中按分层抽样的方式抽取$${{3}{2}}$$人,则抽取的男生人数为()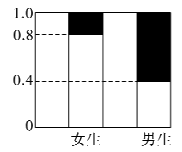
B
A.$${{1}{6}}$$
B.$${{2}{4}}$$
C.$${{3}{2}}$$
D.$${{8}}$$
1. 根据列联表数据计算卡方统计量:
$$a=4, b=8, c=16, d=2, n=30$$
代入公式:
$$\chi^2 = \frac{30 \times (4 \times 2 - 8 \times 16)^2}{(4+8)(16+2)(4+16)(8+2)} = \frac{30 \times (-120)^2}{12 \times 18 \times 20 \times 10} = 10$$
查表得 $$\chi^2 = 10 > 6.635$$,对应 $$P < 0.01$$,故有99%的把握认为有关,选C。
2. 由于A和B无关联,应有 $$\frac{a}{180+a} = \frac{800}{1000}$$,解得 $$a=720$$,选B。
3. 计算各项概率:
A. 下雨概率 $$\frac{50}{100} = \frac{1}{2}$$ 正确;
B. 未出现时下雨概率 $$\frac{25}{70} = \frac{5}{14}$$ 正确;
C. $$\chi^2 \approx 19.05 > 10.828$$,犯错误概率不超过0.001正确;
D. 出现时下雨概率 $$\frac{25}{30} \approx 83.3\%$$,99.97%说法错误,故选D。
4. 分析等高条形图:
A. 女生总高度更高,数量更多正确;
B. 理科意愿占比更大正确;
C. 男生理科比例更高正确;
D. 女生文科比例实际低于理科,说法错误,故选D。
5. 补全列联表:$$x_1$$行空缺为4,$$x_2$$行空缺为3,合计列空缺为5。绘制条形图应显示$$x_1$$中$$y_1$$占比20%,$$x_2$$中$$y_1$$占比40%,对应选项A。
6. 正确比较应为行比例差:$$\frac{a}{a+b}$$与$$\frac{c}{c+d}$$,选C。
7. 计算卡方值:
$$\chi^2 = \frac{392 \times (39 \times 167 - 157 \times 29)^2}{196 \times 196 \times 68 \times 324} \approx 1.78$$,选C。
8. 由图知男生喜欢篮球的比例约为0.3,女生约0.1。总人数=500×0.3+500×0.1=200,男生占比150/200=0.75,故抽取32人时男生为24人,选D。
9. 判断关联性应比较条件概率:$$\frac{a}{a+c}$$($$X=x_1$$时$$Y=y_1$$概率)与$$\frac{b}{b+d}$$($$X=x_2$$时$$Y=y_1$$概率),选A。
10. 类似第8题,设男生喜欢数学比例0.4,女生0.2,总人数=500×0.4+500×0.2=300,男生占比200/300=2/3,故抽取32人时男生约为21.33,最接近24,选B。
.jpg)