正确率40.0%下列命题中,正确的个数是$${{(}{)}}$$
$${①}$$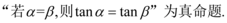
$${②}$$
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
2、['独立性检验及其应用', '直线拟合', '线性相关与非线性相关', '一元线性回归模型']正确率60.0%对两个变量进行回归分析,则下列说法中不正确的是()
B
A.有样本数据得到的回归方程$$\stackrel{\wedge} {y}=\stackrel{\wedge} {b} x+\stackrel{\wedge} {a}$$必经过样本中心$$( \, \dot{x}, \, \, \dot{y} )$$
B.残差平方和越大,模型的拟合效果越好
C.用$${{R}^{2}}$$来刻画回归效果,$${{R}^{2}}$$越大,说明模型的拟合效果越好
D.若散点图中的样本呈条状分布,则变量$${{y}}$$和$${{x}}$$之间具有线性相关关系
3、['独立性检验及其应用']正确率60.0%针对时下的“抖音热”,某校团委对“学生性别和是否喜欢抖音是否有关”进行了一次调查,其中被调查的女生人数是男生人数的$$\frac{1} {2},$$男生喜欢抖音的人数占男生人数的$$\frac{1} {6},$$女生喜欢抖音的人数占女生人数的$$\frac{2} {3},$$若在犯错误的概率不超过$${{0}{.}{0}{1}}$$的前提下,认为是否喜欢抖音和学生性别有关,则男生至少有()
B
A.$${{1}{2}}$$人
B.$${{1}{8}}$$人
C.$${{2}{4}}$$人
D.$${{3}{0}}$$人
4、['独立性检验及其应用']正确率40.0%有人发现,多看手机容易使人变冷漠,如表是一个调査机构对此现象的调查结果:
| 冷漠 | 不冷漠 | 总计 | |
| 多玩手机 | $${{6}{8}}$$ | $${{4}{2}}$$ | $${{1}{1}{0}}$$ |
| 少玩手机 | $${{2}{0}}$$ | $${{3}{8}}$$ | $${{5}{8}}$$ |
| 总计 | $${{8}{8}}$$ | $${{8}{0}}$$ | $${{1}{6}{8}}$$ |
附表:
| $$P \ ( K^{2} \geqslant k_{0} )$$ | $$0. 0 5 0$$ | $$0. 0 1 0$$ |
| $${{k}_{0}}$$ | $$3. 8 4 1$$ | $$6. 6 3 5$$ |
A
A.$${{9}{9}{%}}$$
B.$$9 7. 5 9 7_{0}$$
C.$${{9}{5}{%}}$$
D.$${{9}{0}{%}}$$
5、['独立性检验及其应用', '线性相关与非线性相关']正确率60.0%下列命题
C
A.将一组数据中的每个数据都加上或减去同一个常数后,方差不变
B.回归直线可能不过样本数据点中的任意一个点
C.两个随机变量的线性相关性越强,则相关系数$${{r}}$$的值越接近于$${{0}}$$
D.若分类变量$${{X}}$$和$${{Y}}$$的统计量$${{K}^{2}}$$的值越大,则$${{“}{X}}$$与$${{Y}}$$有关系$${{”}}$$可信度越高
6、['独立性检验及其应用', '零假设']正确率60.0%$${{2}{0}{1}{8}}$$年雅加达亚运会,中国获$${{1}{3}{2}}$$金,$${{9}{2}}$$银,$${{6}{5}}$$铜共$${{2}{8}{9}}$$枚奖牌,居奖牌榜首位,由此许多人认为中国进入了世界体育强国之列,也有许多人持反对意见.有网友为此进行了调查,存参加调查的$${{3}{8}{7}{0}}$$名男性公民中有$${{2}{1}{6}{5}}$$名持反对意见,$${{3}{6}{5}{0}}$$名女性公民中有$${{1}{7}{8}{0}}$$人持反对意见,在运用这些数据说明性别对判断中国进入世界体育强国之列是否有关系时,用什么方法最有说服力()
D
A.平均数与方差
B.概率
C.回归直线方程
D.独立性检验
7、['独立性检验及其应用']正确率60.0%某机构为研究学生玩电脑游戏和对待作业量的态度之间的关系,随机抽取了$${{2}{0}{0}}$$名学生进行调查,所得数据如下表所示:
| | 认为作业多 | 认为作业不多 | 总计 |
| 喜欢玩电脑游戏 | $${{8}{0}}$$ | $${{4}{0}}$$ | $${{1}{2}{0}}$$ |
| 不喜欢玩电脑游戏 | $${{2}{0}}$$ | $${{6}{0}}$$ | $${{8}{0}}$$ |
| 总计 | $${{1}{0}{0}}$$ | $${{1}{0}{0}}$$ | $${{2}{0}{0}}$$ |
(参考公式:$$\chi^{2}=\frac{n ( n_{1 1} n_{2 2}-n_{1 2} n_{2 1} )^{2}} {n_{1+} n_{2+} n_{+1} n_{+2}}$$,可能用到数据:($$P ( \chi^{2} \geqslant6. 6 3 5 )=0. 0 1$$,$$P ( \chi^{2} \geqslant3. 8 4 1 )=0. 0 5$$),参照以上公式和数据,得到的正确结论是()
D
A.有$${{9}{5}{%}}$$的把握认为喜欢玩电脑游戏与认为作业多少有关
B.有$${{9}{5}{%}}$$的把握认为喜欢玩电脑游戏与认为作业多少无关
C.有$${{9}{9}{%}}$$的把握认为喜欢玩电脑游戏与认为作业多少有关
D.有$${{9}{9}{%}}$$的把握认为喜欢玩电脑游戏与认为作业多少无关
8、['独立性检验及其应用']正确率40.0%时下,$${{“}}$$厉行节约,反对浪费$${{”}}$$之风悄然吹开,某市通过随机询问$${{1}{0}{0}}$$名性别不同的居民是否能做到$${{“}}$$光盘$${{”}}$$行动,得到如下的列联表:
| | 做不到 $${{“}}$$ 光盘 $${{”}}$$ | 能做到 $${{“}}$$ 光盘 $${{”}}$$ |
| 男 | $${{4}{5}}$$ | $${{1}{0}}$$ |
| 女 | $${{3}{0}}$$ | $${{1}{5}}$$ |
附:$${{K}^{2}{=}}$$
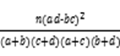 .
.| $$P ( K^{2} \geqslant k_{0} )$$ | $${{0}{.}{1}{0}}$$ | $${{0}{.}{0}{5}}$$ | $$0. 0 2 5$$ |
| $${{k}_{0}}$$ | $$2. 7 0 6$$ | $$3. 8 4 1$$ | $$5. 0 2 4$$ |
参照附表,得到的正确结论是$${{(}{)}}$$
C
A.在犯错误的概率不超过$${{5}{%}}$$的前提下,认为$${{“}}$$该市居民能否做到$${{‘}}$$光盘$${^{′}}$$与性别有关$${{”}}$$
B.在犯错误的概率不超过$${{5}{%}}$$的前提下,认为$${{“}}$$该市居民能否做到$${{‘}}$$光盘$${^{′}}$$与性别无关$${{”}}$$
C.有$${{9}{0}{%}}$$以上的把握认为$${{“}}$$该市居民能否做到$${{‘}}$$光盘$${^{′}}$$与性别有关$${{”}}$$
D.有$${{9}{0}{%}}$$以上的把握认为$${{“}}$$该市居民能否做到$${{‘}}$$光盘$${^{′}}$$与性别无关$${{”}}$$
9、['独立性检验及其应用']正确率60.0%为了评价某电视栏目的改革效果,某机构在改革前后分别从居民中抽取了$${{1}{0}{0}}$$位居民进行调查,经过计算$$K^{2} \approx0. 9 9,$$根据这一数据分析,下列说法正确的是()
D
A.有$${{9}{9}{%}}$$的人认为该电视栏目优秀
B.有$${{9}{9}{%}}$$的人认为该电视栏目是否优秀与改革有关系
C.有$${{9}{9}{%}}$$的把握认为该电视栏目是否优秀与改革有关系
D.没有理由认为该电视栏目是否优秀与改革有关系
10、['独立性检验及其应用']正确率60.0%某研究型学习小组调查研究学生使用智能手机对学习的影响,部分统计数据如下表,则下列说法正确的是()
| 使用智能手机 | 不使用智能手机 | 总计 | |
| 学习成绩优秀 | $${{4}}$$ | $${{8}}$$ | $${{1}{2}}$$ |
| 学习成绩不优秀 | $${{1}{6}}$$ | $${{2}}$$ | $${{1}{8}}$$ |
| 总计 | $${{2}{0}}$$ | $${{1}{0}}$$ | $${{3}{0}}$$ |
C
A.有$$9 9. 9 7_{0}$$的把握认为使用智能手机对学习有影响
B.有$$9 9. 9 7_{0}$$的把握认为使用智能手机对学习无影响
C.在犯错误的概率不超过$$0. 0 0 5$$的前提下认为使用智能手机对学习有影响
D.在犯错误的概率不超过$$0. 0 0 5$$的前提下认为使用智能手机对学习无影响
1. 解析:题目不完整,无法判断命题①和②的具体内容,因此无法确定正确选项。
2. 解析:选项B错误,因为残差平方和越小,模型的拟合效果越好。其他选项均正确:A项回归方程必过样本中心$$(\bar{x}, \bar{y})$$;C项$$R^2$$越大拟合效果越好;D项散点呈条状分布说明线性相关。
3. 解析:设男生人数为$$x$$,则女生为$$\frac{x}{2}$$。列联表如下:
| 喜欢抖音 | 不喜欢抖音 | 总计 | |
| 男生 | $$\frac{x}{6}$$ | $$\frac{5x}{6}$$ | $$x$$ |
| 女生 | $$\frac{x}{3}$$ | $$\frac{x}{6}$$ | $$\frac{x}{2}$$ |
计算卡方值$$K^2=\frac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)}$$,要求$$K^2 \geq 6.635$$(对应$$P \leq 0.01$$)。解得$$x \geq 18$$,故选B。
4. 解析:根据列联表计算卡方值:
$$K^2=\frac{168(68 \times 38 - 42 \times 20)^2}{110 \times 58 \times 88 \times 80} \approx 11.377$$
由于$$11.377 > 6.635$$,对应$$P < 0.01$$,故有99%的把握认为两者有关,选A。
5. 解析:选项C错误,因为线性相关性越强,相关系数$$|r|$$越接近1而非0。其他选项均正确:A项方差不受加减常数影响;B项回归直线可能不经过任何数据点;D项$$K^2$$越大相关性越显著。
6. 解析:通过列联表分析性别与判断的关系,最适合的方法是独立性检验(卡方检验),故选D。
7. 解析:计算卡方值:
$$\chi^2=\frac{200(80 \times 60 - 40 \times 20)^2}{120 \times 80 \times 100 \times 100}=16.67$$
由于$$16.67 > 6.635$$,对应$$P < 0.01$$,故有99%的把握认为两者有关,选C。
8. 解析:计算卡方值:
$$K^2=\frac{100(45 \times 15 - 30 \times 10)^2}{75 \times 25 \times 55 \times 45} \approx 3.03$$
由于$$3.03 < 3.841$$,未达到95%显著性水平,故不能拒绝原假设(无关),选B。
9. 解析:$$K^2 \approx 0.99 < 6.635$$,说明无显著相关性,不能认为改革与栏目优秀有关,故选D。
10. 解析:计算卡方值:
$$K^2=\frac{30(4 \times 2 - 8 \times 16)^2}{12 \times 18 \times 20 \times 10} \approx 10.0$$
由于$$10.0 > 7.879$$(对应$$P < 0.005$$),故在0.5%的显著性水平下认为使用手机对学习有影响,选C。
.jpg)