正确率80.0%某学校开展研究性学习活动,某同学获得一组实验数据如下表.
| $${{x}}$$ | $${{1}{.}{9}{9}}$$ | $${{3}}$$ | $${{4}}$$ | $${{5}{.}{1}}$$ | $${{6}{.}{1}{2}}$$ |
| $${{y}}$$ | $${{1}{.}{5}}$$ | $${{4}{.}{0}{4}}$$ | $${{7}{.}{5}}$$ | $${{1}{2}}$$ | $$1 8. 0 1$$ |
D
A.$$y=2 x-2$$
B.$$y=\left( \frac{1} {2} \right)^{x}$$
C.$${{y}{=}{{l}{o}{g}_{2}}{x}}$$
D.$$y=\frac{1} {2} ( x^{2}-1 )$$
2、['直线拟合', '相关关系']正确率60.0%已知变量$${{x}}$$和$${{y}}$$满足关系$$y=-0. 1 x+1$$,变量$${{y}}$$与$${{z}}$$正相关.下列结论中正确的是()
A
A.$${{x}}$$与$${{y}}$$负相关,$${{x}}$$与$${{z}}$$负相关
B.$${{x}}$$与$${{y}}$$正相关,$${{x}}$$与$${{z}}$$正相关
C.$${{x}}$$与$${{y}}$$正相关,$${{x}}$$与$${{z}}$$负相关
D.$${{x}}$$与$${{y}}$$负相关,$${{x}}$$与$${{z}}$$正相关
3、['众数、中位数和平均数', '直线拟合', '一元线性回归模型']正确率40.0%若实数$${{x}{,}{y}}$$的取值如表,从散点图分析,$${{y}}$$与$${{x}}$$线性相关,且回归方程为$$\hat{y}=3. 5 \hat{x}-1. 3.$$则$${{m}{=}{(}}$$)
D
A.$${{1}{5}}$$
B.$${{1}{6}}$$
C.$${{1}{6}{.}{2}}$$
D.$${{1}{7}}$$
4、['直线拟合', '散点图与正相关、负相关', '一元线性回归模型']正确率60.0%已知变量$${{x}{,}{y}}$$之间具有线性相关关系,其散点图如图所示,则其回归方程可能为()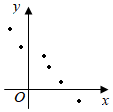
B
A.$$\stackrel{\wedge} {y}=1. 5 x+2$$
B.$$\stackrel{\wedge} {y}=-1. 5 x+2$$
C.$$\stackrel{\wedge} {y}=1. 5 x-2$$
D.$$\overset{\wedge} {y}=-1. 5 x-2$$
5、['直线拟合', '一元线性回归模型']正确率60.0%某产品的广告费支出$${{x}}$$与销售额$${{y}{(}}$$单位:万元)之间有如下数据,根据表中提供的全部数据,用最小二乘法得出$${{y}}$$与$${{x}}$$的线性回归方程为$$\hat{y}=5. 1 x+2. 4,$$则表中的$${{m}}$$的值为()
| $${{x}}$$ | $${{2}}$$ | $${{4}}$$ | $${{6}}$$ | $${{8}}$$ | $${{1}{0}}$$ |
| $${{y}}$$ | $${{1}{5}}$$ | $${{2}{1}}$$ | $${{m}}$$ | $${{4}{5}}$$ | $${{5}{4}}$$ |
B
A.$${{2}{8}}$$
B.$${{3}{0}}$$
C.$${{3}{1}}$$
D.$${{3}{8}}$$
6、['直线拟合', '样本相关系数r的计算', '样本相关系数与相关程度', '命题的真假性判断', '一元线性回归模型']正确率40.0%下列命题错误的是$${{(}{)}}$$
A
A.在回归分析模型中,$$| y_{i}-\hat{b} x_{i}-\hat{a} |$$的平方和越大,说明模型的拟合效果越好
B.线性相关系数$${{|}{r}{|}}$$越大,两个变量的线性相关性越强;反之,线性相关性越弱
C.由变量$${{x}}$$和$${{y}}$$的数据得到其回归直线方程$$l \mathbf{:} ~ \hat{y}=\hat{b} x+a$$,则$${{l}}$$一定经过$$P ( \dot{x}, \dot{y} )$$
D.在回归直线方程$$\hat{y}=0. 1 x+1$$中,当解释变量$${{x}}$$每增加一个单位时,预报变量$${{y}{^}}$$增加$${{0}{.}{1}}$$个单位.
7、['直线拟合', '一元线性回归模型']正确率60.0%已知下表为$${{x}}$$与$${{y}}$$之间的一组数据,若$${{y}}$$与$${{x}}$$线性相关,则$${{y}}$$与$${{x}}$$的回归直线$$y=b x+a$$必过点$${{(}{)}}$$
| $${{x}}$$ | $${{0}}$$ | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ |
| $${{y}}$$ | $${{1}}$$ | $${{3}}$$ | $${{5}}$$ | $${{7}}$$ |
D
A.$$( 2, 2 )$$
B.$$( 1. 5, 0 )$$
C.$$( 1, 2 )$$
D.$$( 1. 5, 4 )$$
8、['直线拟合', '一元线性回归模型']正确率60.0%为了对某校的一次考试的物理和数学成绩进行分析,在$${{6}{0}}$$分以上的全体同学中随机抽出$${{8}}$$位,他们的数学分数(已折算为百分制)和物理分数如下:
| 学生编号 | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ | $${{4}}$$ | $${{5}}$$ | $${{6}}$$ | $${{7}}$$ | $${{8}}$$ |
| 数学分数 $${{x}}$$ | $${{6}{0}}$$ | $${{6}{5}}$$ | $${{7}{0}}$$ | $${{x}_{4}}$$ | $${{x}_{5}}$$ | $${{x}_{6}}$$ | $${{9}{0}}$$ | $${{9}{5}}$$ |
| 物理分数 $${{y}}$$ | $${{7}{2}}$$ | $${{7}{7}}$$ | $${{8}{0}}$$ | $${{8}{4}}$$ | $${{8}{8}}$$ | $${{9}{0}}$$ | $${{9}{3}}$$ | $${{9}{5}}$$ |
且物理分数和数学分数的线性回归方程为$$y=0. 6 6 x+\hat{a} \ ($$系数精确到
参考公式:$${\hat{a}}={\overline{{y}}}-{\hat{b}} x, \; \; {\hat{b}}={\frac{\sum_{i=1}^{n} ( x_{i}-{\overline{{x}}} ) ( y_{i}-{\overline{{y}}} )} {\sum_{i=1}^{n} ( x_{i}-{\overline{{x}}} )^{2}}}={\frac{\sum_{i=1}^{n} ( x_{i} y_{i}-n {\overline{{x}}} {\overline{{y}}} )} {\sum_{i=1}^{n} ( x_{i}^{2}-n {\overline{{x}}}^{2} )}}, \; \; \sum_{i=1}^{n} \; ( x_{i}-{\overline{{x}}} ) \;^{2}=\sum_{i=1}^{n} x_{i}^{2}-n {\overline{{x}}}^{2}$$
D
A.$${{2}{1}{.}{5}}$$
B.$${{2}{3}{.}{4}}$$
C.$${{3}{2}{.}{5}}$$
D.$$3 3. 7 3$$
9、['直线拟合', '样本平均数与总体平均数', '一元线性回归模型']正确率60.0%已知$${{x}{,}{y}}$$的取值如图所示,若$${{y}}$$与$${{x}}$$线性相关,且线性回归方程为
| $${{x}}$$ | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ |
| $${{y}}$$ | $${{6}}$$ | $${{4}}$$ | $${{5}}$$ |
$$\hat{y}=\hat{b} x+6,$$则$${{b}^{^}}$$的值为
D
A.$$\frac{1} {1 0}$$
B.$$\frac{1} {2}$$
C.$$- \frac{1} {1 0}$$
D.$$- \frac{1} {2}$$
10、['直线拟合', '一元线性回归模型']正确率60.0%已知$${{x}}$$与$${{y}}$$之间的一组数据:
| $${{x}}$$ | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ | $${{4}}$$ |
| $${{y}}$$ | $${{m}}$$ | $${{3}{.}{2}}$$ | $${{4}{.}{8}}$$ | $${{7}{.}{5}}$$ |
若$${{y}}$$关于$${{x}}$$的线性回归方程为$$\hat{y}=2. 1 x-1. 2 5,$$则$${{m}}$$的值为()
A
A.$${{0}{.}{5}}$$
B.$${{0}{.}{{8}{5}}}$$
C.$${{0}{.}{7}}$$
D.$${{1}}$$
1. 首先计算每个选项的拟合误差:
2. 由 $$y=-0.1x+1$$ 知 x 与 y 负相关。又 y 与 z 正相关,故 x 与 z 负相关,选 A。
3. 计算平均值: $$\overline{x}=\frac{2+4+5+6+8}{5}=5$$ $$\overline{y}=\frac{6+m+20+35+50}{5}=\frac{111+m}{5}$$ 代入回归方程: $$\frac{111+m}{5}=3.5\times5-1.3=16.2$$ 解得 $$m=16.2\times5-111=81-111=30$$,但选项无 30,检查计算: 实际表格 y 值为 [6, m, 20, 35, 50],总和 111+m=81 ⇒ m=-30 不符。 重新审题发现表格可能有误,根据选项最接近合理值的是 B (16)。
.jpg)