正确率80.0%在回归分析中,体现数据点和它在经验回归直线上相应位置的差异的是()
B
A.截距参数
B.残差平方和
C.斜率参数
D.样本相关系数
2、['决定系数R^2', '残差', '散点图与正相关、负相关']正确率60.0%甲、乙、丙、丁$${{4}}$$位同学各自对$${{x}{,}{y}}$$两个变量进行回归分析,分别得到散点图与残差平方和$$\sum_{i=1}^{n} ( y_{i}-\hat{y}_{i} )^{2}$$如下表:
| 甲 | 乙 | 丙 | 丁 | |
| 散点图 | 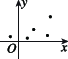 |  | 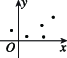 | 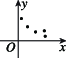 |
| 残差平方和 | $${{1}{1}{5}}$$ | $${{1}{0}{6}}$$ | $${{1}{2}{4}}$$ | $${{1}{0}{3}}$$ |
D
A.甲
B.乙
C.丙
D.丁
3、['残差']正确率80.0%下面四个残差图中可反映出一元线性回归模型拟合精度较好的为()
A
A.
B.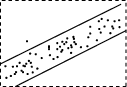
C.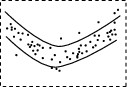
D.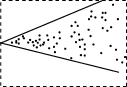
正确率80.0%已知回归方程$$\hat{y}=2 x-1,$$则该方程在样本$$( 3, 4 )$$处的残差为()
D
A.$${{5}}$$
B.$${{2}}$$
C.$${{1}}$$
D.$${{−}{1}}$$
5、['残差', '直线拟合', '命题的真假性判断']正确率40.0%有下列说法:
$${①}$$在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;
$${②}$$用相关指数$${{R}^{2}}$$来刻画回归的效果,$${{R}^{2}}$$值越大,说明模型的拟合效果越好;
$${③}$$比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型,拟合效果越好.
$${④}$$在研究气温和热茶销售杯数的关系时,若求得相关指数$${{R}^{2}{≈}{{0}{.}{8}{5}}}$$,则表明气温解释了$${{1}{5}{%}}$$的热茶销售杯数变化.
其中正确命题的个数是()
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
6、['方差与标准差', '列联表', '决定系数R^2', '残差', '样本相关系数与相关程度', '命题的真假性判断']正确率60.0%已知下列命题:
$${①}$$常用等高条形图来展示列联表数据的频率特征
$${②}$$两个变量相关性越强,则相关系数$${{r}}$$就越接近于$${{1}}$$;
$${③}$$将一组数据中的每个数据都加上一个相同的常数后,方差不变
$${④}$$在线性回归模型中,相关指数$${{R}^{2}}$$表示解释变量$${{x}}$$对于预报变量$${{y}}$$的贡献率,$${{R}^{2}}$$越接近于$${{1}}$$,表示回归效果越好;
$${⑤}$$残差点比较均匀的落在水平的带状区域中,说明选用的模型比较合适,并且这样的带状区域越宽,说明模型的拟合精度越高
则正确命题的个数是()
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
7、['决定系数R^2', '残差']正确率60.0%对于给定的样本点所建立的模型$${{A}}$$和模型$${{B}}$$,它们的残差平方和分别是$$a_{1}, a_{2}, ~ R^{2}$$的值分别为$${{b}_{1}{,}{{b}_{2}}}$$,下列说法正确的是$${}$$
C
A.若$${{a}_{1}{<}{{a}_{2}}}$$,则$$b_{1} < b_{2}, \, \, A$$的拟合效果更好
B.若$${{a}_{1}{<}{{a}_{2}}}$$,则$$b_{1} < b_{2}, ~ B$$的拟合效果更好
C.若$${{a}_{1}{<}{{a}_{2}}}$$,则$$b_{1} > b_{2}, \ A$$的拟合效果更好
D.若$${{a}_{1}{<}{{a}_{2}}}$$,则$$b_{1} > b_{2}, \ B$$的拟合效果更好
8、['直线拟合', '残差', '样本相关系数与相关程度']正确率60.0%下列叙述正确的个数为$${{(}{)}}$$
$${{(}{1}{)}}$$残差的平方和越小,即模型的拟合效果越好
$${{(}{2}{)}{{R}^{2}}}$$越大,即模型的拟合效果越好
$${{(}{3}{)}}$$回归直线过样本点的中心.
B
A.$${{0}}$$
B.$${{3}}$$
C.$${{2}}$$
D.$${{1}}$$
9、['独立性检验及其应用', '直线拟合', '残差', '样本相关系数与相关程度', '命题的真假性判断', '一元线性回归模型']正确率40.0%已知下列命题:
$${①}$$回归直线$$\stackrel{\wedge} {y}=\stackrel{\wedge} {b} x+\stackrel{\wedge} {a}$$恒过样本点的中心$$( \overline{{x}}, \overline{{y}} )$$,且至少过一个样本点;
$${②}$$两个变量相关性越强,则相关系数$${{r}}$$就越接近于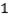 ;
;
$${③}$$
B
A.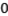
B.
C.
D.
正确率60.0%有以下四个命题:
$${①}$$在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;
$${②}$$对分类变量$${{x}}$$与$${{y}}$$的随机变量$${{K}^{2}}$$的观测值$${{k}}$$来说,$${{k}}$$越小,判断$${{“}{x}}$$与$${{y}}$$有关系$${{”}}$$的把握越大;
$${③}$$若数据$$x_{1}, ~ x_{2}, ~ \dots, ~ x_{n}$$的方差为$${{2}}$$,则$$2 x_{1}, \ 2 x_{2}, \ \ldots\ 2 x_{n}$$的方差为$${{8}}$$;
$${④}$$两个变量的线性相关性越强,相关系数的绝对值越接近于$${{0}}$$.
其中真命题的个数为()
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
1. 在回归分析中,数据点与经验回归直线上相应位置的差异由残差平方和衡量。残差平方和越小,拟合效果越好。因此,正确答案是:
2. 拟合精度由残差平方和衡量,残差平方和越小,拟合精度越高。丁的残差平方和最小(103),因此拟合精度最高。正确答案是:
3. 一元线性回归模型拟合精度较好的残差图应满足残差均匀分布在水平带状区域内,无明显规律性。选项A的残差分布均匀且无趋势,因此正确答案是:
4. 残差的计算公式为 $$e_i = y_i - \hat{y}_i$$。对于样本点 $$(3, 4)$$,回归方程预测值为 $$\hat{y} = 2 \times 3 - 1 = 5$$,残差为 $$4 - 5 = -1$$。正确答案是:
5. 分析各命题:
① 正确,残差均匀分布在带状区域内说明模型合适;
② 正确,$$R^2$$ 越大,拟合效果越好;
③ 正确,残差平方和越小,拟合效果越好;
④ 错误,$$R^2 \approx 0.85$$ 表示气温解释了85%的热茶销售杯数变化。
因此,正确命题有3个。正确答案是:
6. 分析各命题:
① 正确,等高条形图常用于展示列联表数据的频率;
② 错误,相关系数 $$r$$ 越接近1或-1,相关性越强,但不一定接近1;
③ 正确,数据加减常数不改变方差;
④ 正确,$$R^2$$ 越接近1,回归效果越好;
⑤ 错误,带状区域越窄,拟合精度越高。
因此,正确命题有3个。正确答案是:
7. 残差平方和越小,$$R^2$$ 越大,拟合效果越好。若 $$a_1 < a_2$$,则 $$b_1 > b_2$$,模型A的拟合效果更好。正确答案是:
8. 分析各叙述:
(1) 正确,残差平方和越小,拟合效果越好;
(2) 正确,$$R^2$$ 越大,拟合效果越好;
(3) 正确,回归直线过样本点中心 $$(\overline{x}, \overline{y})$$。
因此,全部叙述正确。正确答案是:
9. 题目不完整,无法解析。
10. 分析各命题:
① 正确,残差均匀分布在带状区域内说明模型合适;
② 错误,$$k$$ 越大,判断“$$x$$ 与 $$y$$ 有关系”的把握越大;
③ 正确,数据乘以2后方差为 $$2 \times 2^2 = 8$$;
④ 错误,线性相关性越强,相关系数的绝对值越接近1。
因此,真命题有2个。正确答案是:
.jpg)