残差-8.2 一元线性回归模型及其应用知识点教师选题进阶单选题自测题答案-广西壮族自治区等高三数学选择必修,平均正确率54.0%

正确率60.0%根据一组样本数据$$( x_{1}， ~ y_{1} )， ~ ( x_{2}， ~ y_{2} )， ~ \dots， ~ ( x_{n}， ~ y_{n} )，$$求得经验回归方程为$$\hat{y}=1. 2 x+0. 4，$$且$$\overline{{x}}=3$$.现发现这组样本数据中有两个样本点$$( 1. 2， ~ 0. 5 )$$和$$( 4. 8， ~ 7. 5 )$$误差较大，去除后重新求得的经验回归直线的斜率为$${{1}{.}{1}{，}}$$则（）

C

A.去除两个误差较大的样本点后$${，{y}}$$的估计值增加速度变快

B.去除两个误差较大的样本点后，重新求得的经验回归方程对应的直线一定过点$$( 3， \ 5 )$$

C.去除两个误差较大的样本点后，重新求得的经验回归方程为$$\hat{y}=1. 1 x+0. 7$$

D.去除两个误差较大的样本点后，相应于样本点$$( 2， ~ 2. 7 )$$的残差为$${{0}{.}{1}}$$

正确率60.0%为了表示散点图中$${{n}}$$个点与某一条直线在整体上的接近程度，我们常用下面四个量中的（）

C

A.$$\sum_{i=1}^{n} ( y_{i}-\hat{y}_{i} )$$

B.$$\sum_{i=1}^{n} ( \hat{y}_{i}-y_{i} )$$

C.$$\sum_{i=1}^{n} \left( \begin{array} {c} {y_{i}} \\ \end{array} \right) \sum_{i=1}^{2}$$

D.$$\sum_{i=1}^{n} \left( \hat{y}_{i}-y_{i} \right)^{2}$$

正确率60.0%$$a， ~ b， ~ c， ~ d$$四位同学各自对甲$${、}$$乙两变量做回归分析，分别得到散点图与残差平方和$$\sum_{i=1}^{n} ( y_{i}-\hat{y}_{i} )^{2}$$如下表：

	$${{a}}$$	$${{b}}$$	$${{c}}$$	$${{d}}$$
散点图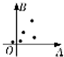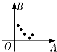
残差平方和	$${{1}{1}{5}}$$	$${{1}{0}{6}}$$	$${{1}{2}{4}}$$	$${{1}{0}{3}}$$

D

A.$${{a}}$$

B.$${{b}}$$

C.$${{c}}$$

D.$${{d}}$$

正确率40.0%下列说法错误的是$${{(}{)}}$$

B

A.自变量取值一定时，因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系

B.线性回归方程对应的直线$$\hat{y}=\hat{b} x+\hat{a}，$$至少经过其样本数据点$$( x_{1}， y_{1} )， ~ ( x_{2}， y_{2} )， ~ \dots， ~ ( x_{n}， y_{n} )$$中的一个点

C.在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高

D.在回归分析中，$${{R}^{2}}$$为$${{0}{.}{9}{8}}$$的模型比$${{R}^{2}}$$为$${{0}{.}{8}{0}}$$的模型拟合的效果好

正确率60.0%某产品的广告费支出$${{x}}$$与销售额$${{y}{(}}$$单位：万元)之间的关系如表，由此得到$${{y}}$$与$${{x}}$$的线性回归方程为$$\hat{y}=6 x+a，$$由此可得：当广告支出$${{5}}$$万元时，随机误差的效应(残差)为$${{(}{)}}$$

C

A.$${{−}{{1}{0}}}$$

B.$${{0}}$$

C.$${{1}{0}}$$

D.$${{2}{0}}$$

正确率60.0%已知方程$$y=0. 8 5 x-8 5. 7$$是根据女大学生的身高预报体重的回归方程，其中$${{x}{，}{y}}$$的单位分别是$$\mathit{c m，} \ k g$$，则该方程在样本$$( 1 6 5， 5 7 )$$处的残差是$${{(}{)}}$$

B

A.$$5 4. 5 5$$

B.$${{2}{.}{4}{5}}$$

C.$${{3}{.}{4}{5}}$$

D.$$1 1 1. 5 5$$

正确率40.0%下列说法正确的有（）个
$${①}$$在刻画回归模型的拟合效果时，$${{R}^{2}}$$越大，说明拟合的效果越好．
$${②}$$在回归分析中残差图的纵坐标为残差．
$${③}$$独立性检测中，等高条形图可以粗略地判断两个分类变量是否相关．
$${④}$$在列联表中，$$\frac{a} {a+b}$$与$$\frac{c} {c+d}$$相差越大，两个分类变量之间的关系越强．

D

A.$${{1}}$$

B.$${{2}}$$

C.$${{3}}$$

D.$${{4}}$$

正确率40.0%在下列命题中，真命题的个数是$${{(}{)}}$$
$${①}$$若$${{K}^{2}}$$的观测值为$$k=6. 6 3 5$$，我们有$${{9}{9}{%}}$$的把握认为吸烟与患肺病有关系，那么在$${{1}{0}{0}}$$个吸烟的人中必有$${{9}{9}}$$人患有肺病；
$${②}$$ 由样本数据得到的回归直线$$\hat{y}=\hat{b} x+\widehat{a}$$ 必过样本点的中心$$( \overline{{x}}， \overline{{y}} )$$ ；
$${③}$$ 残差平方和越小的模型，拟合的效果越好；
$${④}$$ 若复数 $${{z}{=}{m}}$$$${^{2}}$$ $$- 1+( m+1 ) i$$ 为纯虚数，则实数 $${{m}{=}{±}{1}}$$ 。

C

A.$${{0}}$$

B.$${{1}}$$

C.$${{2}}$$

D.$${{3}}$$

正确率60.0%如图所示，$${{5}}$$组数据$$( x， y )$$中去掉$$D ( 3， 1 0 )$$后，下列说法错误的是（）
​

B

A.相关系数$${{r}}$$变大

B.残差平方和变大

C.相关指数$${{R}^{2}}$$变大

D.解释变量$${{x}}$$与预报变量$${{y}}$$的相关性变强

正确率60.0%下列说法正确的是（）

B

A.若残差平方和越小，则相关指数$${{R}^{2}}$$越小

B.将一组数据中每一个数据都加上或减去同一常数，方差不变

C.若$${{K}^{2}}$$的观测值越大，则判断两个分类变量有关系的把握程度越小

D.若所有样本点均落在回归直线上，则相关系数$${{r}{=}{1}}$$

1、首先计算原始回归直线的截距。已知$$\overline{x}=3$$，代入回归方程$$\hat{y}=1.2x+0.4$$，得到$$\overline{y}=1.2 \times 3 + 0.4 = 4$$。去除两个异常点后，斜率变为1.1，新的回归直线形式为$$\hat{y}=1.1x + a$$。由于回归直线必过样本均值点$$(3, \overline{y'})$$，需要重新计算$$\overline{y'}$$。原始样本总和为$$n \times 4$$，去除两个点后总和为$$4n - (0.5 + 7.5) = 4n - 8$$，样本数变为$$n-2$$，因此$$\overline{y'} = \frac{4n - 8}{n-2} = 4$$。代入$$(3, 4)$$到新回归直线，得$$4 = 1.1 \times 3 + a$$，解得$$a = 0.7$$，所以新方程为$$\hat{y}=1.1x + 0.7$$。验证选项：

2、衡量整体接近程度的量是残差平方和，即选项$$D$$。其他选项：

3、拟合精度由残差平方和衡量，越小越好。表中$$d$$的残差平方和最小（103），因此拟合效果最好。

4、错误说法分析：

5、先计算回归方程参数。均值$$\overline{x}=5$$，$$\overline{y}=50$$，代入$$\hat{y}=6x+a$$得$$50=6 \times 5 + a$$，解得$$a=20$$。当$$x=5$$时，预测值$$\hat{y}=6 \times 5 + 20 = 50$$，实际值$$y=60$$，残差为$$60 - 50 = 10$$。

6、残差计算：预测值$$\hat{y}=0.85 \times 165 - 85.7 = 54.55$$，残差为$$57 - 54.55 = 2.45$$。

7、判断各命题：

8、真命题判断：

9、去掉离群点$$D(3,10)$$后：

10、正确选项分析：