非线性回归模型分析-8.2 一元线性回归模型及其应用知识点考前进阶选择题自测题解析-福建省等高三数学选择必修,平均正确率54.0%

1、['非线性回归模型分析'， '命题的真假性判断']

正确率40.0%以下四个命题中是真命题的是

A.对分类变量$${{x}}$$与$${{y}}$$的随机变量$${{k}^{2}}$$的观测值$${{k}}$$来说，$${{k}}$$越小，判断$${{“}{x}}$$与$${{y}}$$有关系$${{”}}$$的把握程度越大

B.两个随机变量的线性相关性越强，相关系数的绝对值越接近于$${{0}}$$

C.若数据$$x_{1}， x_{2}， x_{3}， \dots x_{n}$$，的方差为$${{1}}$$，则$$2 x_{1}， 2 x_{2}， 2 x_{3}， \dots2 x_{n}$$，的方差为$${{2}}$$

D.在回归分析中，可用相关指数$${{R}^{2}}$$的值判断模型的拟合效果，$${{R}^{2}}$$越大，模型的拟合效果越好．

2、['非线性回归模型分析']

正确率60.0%某企业推出了一款新食品，为了解该食品中某种营养成分的含量$${{x}}$$(单位：克)与顾客的满意率$${{y}}$$的关系，通过调查研究发现可选择函数模型$$y=\frac{1} {1 0 0} \mathrm{e}^{k x+c}$$来拟合$${{y}}$$与$${{x}}$$的关系，根据以下数据可求得$${{y}}$$关于$${{x}}$$的回归方程为（）

营养成分含量 $${{x}{/}}$$ 克	$${{1}}$$	$${{2}}$$	$${{3}}$$	$${{4}}$$	$${{5}}$$
$$\operatorname{l n} ( 1 0 0 y )$$	$${{4}{.}{3}{4}}$$	$${{4}{.}{3}{6}}$$	$${{4}{.}{4}{4}}$$	$${{4}{.}{4}{5}}$$	$${{4}{.}{5}{1}}$$

A.$$y=\frac{1} {1 0 0} \mathrm{e}^{0. 0 4 3 x+4. 2 9 1}$$

B.$$y=\frac{1} {1 0 0} \mathrm{e}^{0. 0 4 3 x-4. 2 9 1}$$

C.$$y=\mathrm{e}^{0. 0 4 3 x+4. 2 9 1}$$

D.$$y=\mathrm{e}^{0. 0 4 3 x-4. 2 9 1}$$

3、['非线性回归模型分析']

正确率60.0%某科技公司为加强研发能力，研发费用逐年增加，最近$${{6}}$$年的研发费用$${{y}}$$(单位：亿元)与年份编号$${{x}}$$的样本数据为$$( x_{i}， ~ y_{i} ) ( i=1， ~ 2， ~ 3， ~ 4， ~ 5， ~ 6 )，$$令$$z_{i}=\operatorname{l n} \! y_{i}，$$并将$$( x_{i}， \， \， z_{i} )$$绘制成如图所示的散点图.若$${{y}}$$关于$${{x}}$$的回归方程为$$\hat{y}=\hat{\mathrm{a}} \mathrm{e}^{\hat{b} x}，$$则（）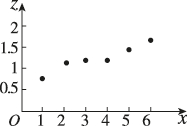

A.$$\widehat{a}$$

B.$$\widehat{a} > 1， ~ ~ \widehat{b} < 0$$

C.$$0 < \widehat{a} < 1， \， \， \， \hat{b} > 0$$

D.$$0 < \widehat{a} < 1， \; \widehat{b} < 0$$

4、['非线性回归模型分析']

正确率40.0%用模型$$y=c \mathrm{e}^{k x}$$拟合一组数据时，为了求出非线性经验回归方程，令$$z=\operatorname{l n} \! y，$$变换后得到经验回归方程$$\hat{z}=0. 5 x+2，$$则$${{c}{ˆ}{=}}$$（）

A.$${{0}{.}{5}}$$

B.$$\mathrm{e}^{0. 5}$$

C.$${{2}}$$

D.$${{e}^{2}}$$

5、['非线性回归模型分析']

正确率40.0%中国是茶的故乡，也是茶文化的发源地.为了弘扬中国茶文化，某酒店推出特色茶食品“金萱排骨茶”，为了了解每壶“金萱排骨茶”中所放茶叶量$${{x}}$$(克)与食客的满意率$${{y}}$$的关系，通过试验调查研究，发现可选择函数模型$$y=a \mathrm{e}^{b x+c}$$来拟合$${{y}}$$与$${{x}}$$的关系，并得到以下数据：

茶叶量 $${{x}}$$ (克)	$${{1}}$$	$${{2}}$$	$${{3}}$$	$${{4}}$$	$${{5}}$$
$$\operatorname{l n} ( 1 0 0 y )$$	$${{4}{.}{3}{4}}$$	$${{4}{.}{3}{6}}$$	$${{4}{.}{4}{4}}$$	$${{4}{.}{4}{5}}$$	$${{4}{.}{5}{1}}$$

则可求得$${{y}}$$关于$${{x}}$$的经验回归方程为（）

A.$$\hat{y}=\frac{1} {1 0 0} \mathrm{e}^{0. 0 4 3 x+4. 2 9 1}$$

B.$$\hat{y}=\frac{1} {1 0 0} \mathrm{e}^{0. 0 4 3 x-4. 2 9 1}$$

C.$$\hat{y}=\mathrm{e}^{0. 0 4 3 x+4. 2 9 1}$$

D.$$\hat{y}=\mathrm{e}^{0. 0 4 3 x-4. 2 9 1}$$

6、['非线性回归模型分析'， '一元线性回归模型']

正确率60.0%以模型$$y=c \mathrm{e}^{k x}$$去拟合一组数据时，为了求出经验回归方程，设$$z=\operatorname{l n} \! y，$$变换后得到的经验回归方程为$$z=0. 5 x+3，$$则$${{c}{=}}$$（）

A.$${{3}}$$

B.$${{e}^{3}}$$

C.$${{0}{.}{5}}$$

D.$$\mathrm{e}^{0. 5}$$

7、['非线性回归模型分析']

正确率60.0%已知两个随机变量$${{x}{，}{y}}$$呈现非线性关系.为了进行线性回归分析，设$$u=2 \mathrm{l n} y， v=( 2 x-3 )^{2}，$$利用最小二乘法，得到经验回归方程$$\hat{u}=-\frac{1} {3} \hat{v}+2$$，则（）

A.变量$${{y}}$$的估计值的最大值为$${{e}}$$

B.变量$${{y}}$$的估计值的最小值为$${{e}}$$

C.变量$${{y}}$$的估计值的最大值为$${{e}^{2}}$$

D.变量$${{y}}$$的估计值的最小值为$${{e}^{2}}$$

8、['非线性回归模型分析'， '一元线性回归模型']

正确率60.0%已知变量$${{x}{，}{y}}$$线性相关，且由观测数据算得样本平均数为$$\overline{{x}}=2， \， \， \， \overline{{y}}=5，$$则由该观测数据得到的线性回归直线方程不可能是（）

A.$$y=2. 1 x+0. 8$$

B.$$y=-1. 2 x+7. 4$$

C.$$y=2. 2 5 x+0. 5$$

D.$$y=-1. 2 5 x+7. 5 5$$

9、['非线性回归模型分析'， '一元线性回归模型']

正确率60.0%今有一组数据如表所示：

$${{x}}$$	$${{1}}$$	$${{2}}$$	$${{3}}$$	$${{4}}$$	$${{5}}$$
$${{y}}$$	$${{3}}$$	$${{5}}$$	$${{6}{.}{9}{9}}$$	$${{9}{.}{0}{1}}$$	$${{1}{1}}$$

下列函数模型中，能最接近地表示这组数据满足规律的是（）

A.$$y=2^{x}+1$$

B.$$y=l o g_{2} ~ ( \ x+7 )$$

C.$$y=x^{2}-x+3$$

D.$$y=2 x+1$$

10、['非线性回归模型分析']

正确率60.0%在一次数学测验中，采集到如下一组数据

$${{x}}$$	$${{−}{2}}$$	$${{−}{1}}$$	$${{0}}$$	$${{1}}$$	$${{2}}$$	$${{3}}$$
$${{y}}$$	$${{0}{.}{2}{4}}$$	$${{0}{.}{5}{1}}$$	$${{1}}$$	$${{2}{.}{0}{2}}$$	$${{3}{.}{9}{8}}$$	$${{8}{.}{0}{2}}$$

则下列函数与$${{x}{、}{y}}$$的函数关系最接近的是(其中$${{a}{、}{b}}$$是待定系数$${{)}{（}}$$）

A.$$y=a x+b$$

B.$$y=a+b^{x}$$

C.$$y=a x^{2}+b$$

D.$$y=a+\frac{b} {x}$$

1. 解析：

选项A错误，因为$$k^2$$的观测值$$k$$越小，判断“$$x$$与$$y$$有关系”的把握程度越小。

选项B错误，因为两个随机变量的线性相关性越强，相关系数的绝对值越接近于$$1$$。

选项C错误，因为若数据$$x_1, x_2, \dots, x_n$$的方差为$$1$$，则$$2x_1, 2x_2, \dots, 2x_n$$的方差为$$4$$。

选项D正确，因为在回归分析中，$$R^2$$越大，模型的拟合效果越好。

正确答案是D。

2. 解析：

给定模型$$y=\frac{1}{100}e^{kx+c}$$，取对数得$$\ln(100y) = kx + c$$。

根据表格数据，对$$\ln(100y)$$和$$x$$进行线性回归，计算斜率$$k$$和截距$$c$$。

通过最小二乘法拟合，得到$$k \approx 0.043$$，$$c \approx 4.291$$。

因此回归方程为$$y=\frac{1}{100}e^{0.043x+4.291}$$。

正确答案是A。

3. 解析：

给定回归模型$$\hat{y} = \hat{a}e^{\hat{b}x}$$，取对数得$$\ln \hat{y} = \ln \hat{a} + \hat{b}x$$。

从散点图可以看出，$$\ln y$$随$$x$$的增加而增加，因此$$\hat{b} > 0$$。

截距$$\ln \hat{a}$$的值决定了$$\hat{a}$$的大小，由图可知$$\ln \hat{a}$$在$$0$$附近，因此$$0 < \hat{a} < 1$$。

正确答案是C。

4. 解析：

给定模型$$y=ce^{kx}$$，取对数得$$\ln y = \ln c + kx$$。

题目中$$\hat{z} = 0.5x + 2$$，对应$$\ln \hat{y} = 0.5x + 2$$。

因此$$\ln c = 2$$，即$$c = e^2$$。

正确答案是D。

5. 解析：

与第2题相同，模型为$$y=a e^{bx+c}$$，取对数得$$\ln y = \ln a + bx + c$$。

根据表格数据，拟合得到$$b \approx 0.043$$，$$\ln a + c \approx 4.291$$。

由于$$a$$和$$c$$的具体值无法分离，但题目选项与第2题一致，因此正确答案是A。

6. 解析：

与第4题类似，给定模型$$y=ce^{kx}$$，取对数得$$\ln y = \ln c + kx$$。

题目中$$z = 0.5x + 3$$，对应$$\ln y = 0.5x + 3$$。

因此$$\ln c = 3$$，即$$c = e^3$$。

正确答案是B。

7. 解析：

给定$$u = 2 \ln y$$，$$v = (2x-3)^2$$，回归方程为$$\hat{u} = -\frac{1}{3}\hat{v} + 2$$。

代入得$$2 \ln \hat{y} = -\frac{1}{3}(2x-3)^2 + 2$$，即$$\ln \hat{y} = -\frac{1}{6}(2x-3)^2 + 1$$。

当$$(2x-3)^2 = 0$$时，$$\ln \hat{y}$$取得最大值$$1$$，此时$$\hat{y} = e$$。

因此变量$$y$$的估计值的最大值为$$e$$。

正确答案是A。

8. 解析：

回归直线必须经过样本均值点$$(\overline{x}, \overline{y}) = (2, 5)$$。

验证选项：

A：$$y=2.1 \times 2 + 0.8 = 5$$，符合。

B：$$y=-1.2 \times 2 + 7.4 = 5$$，符合。

C：$$y=2.25 \times 2 + 0.5 = 5$$，符合。

D：$$y=-1.25 \times 2 + 7.55 = 5.05 \neq 5$$，不符合。

正确答案是D。

9. 解析：

观察数据点$$(1,3)$$, $$(2,5)$$, $$(3,6.99)$$, $$(4,9.01)$$, $$(5,11)$$，近似呈线性关系。

选项D的线性函数$$y=2x+1$$与数据点最接近。

正确答案是D。

10. 解析：

观察数据点$$(-2,0.24)$$, $$(-1,0.51)$$, $$(0,1)$$, $$(1,2.02)$$, $$(2,3.98)$$, $$(3,8.02)$$，$$y$$随$$x$$的增长呈指数趋势。

选项B的指数函数$$y=a+b^x$$最符合数据规律。

正确答案是B。

_{题目来源于各渠道收集，若侵权请联系下方邮箱}