正确率40.0%以下四个命题中是真命题的是
D
A.对分类变量$${{x}}$$与$${{y}}$$的随机变量$${{k}^{2}}$$的观测值$${{k}}$$来说,$${{k}}$$越小,判断$${{“}{x}}$$与$${{y}}$$有关系$${{”}}$$的把握程度越大
B.两个随机变量的线性相关性越强,相关系数的绝对值越接近于$${{0}}$$
C.若数据$$x_{1}, x_{2}, x_{3}, \dots x_{n}$$,的方差为$${{1}}$$,则$$2 x_{1}, 2 x_{2}, 2 x_{3}, \dots2 x_{n}$$,的方差为$${{2}}$$
D.在回归分析中,可用相关指数$${{R}^{2}}$$的值判断模型的拟合效果,$${{R}^{2}}$$越大,模型的拟合效果越好.
2、['非线性回归模型分析']正确率80.0%如图是某种豆类的生长枝数$${{y}}$$与时间$${{t}}$$$${{(}}$$单位:月$${{)}}$$的散点图,那么此种豆类的生长枝数与时间的关系用下列函数模型近似刻画最好的是()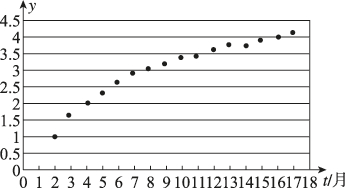
B
A.$${{y}{=}{2}{{t}^{2}}}$$
B.$${{y}{=}{{l}{o}{g}_{2}}{t}}$$
C.$${{y}{=}{{t}^{3}}}$$
D.$${{y}{=}{{2}^{t}}}$$
3、['非线性回归模型分析']正确率40.0%用模型$$y=c \mathrm{e}^{k x}$$拟合一组数据时,为了求出非线性经验回归方程,令$$z=\operatorname{l n} \! y,$$变换后得到经验回归方程$$\hat{z}=0. 5 x+2,$$则$${{c}{ˆ}{=}}$$()
D
A.$${{0}{.}{5}}$$
B.$$\mathrm{e}^{0. 5}$$
C.$${{2}}$$
D.$${{e}^{2}}$$
4、['非线性回归模型分析', '统计分析的应用', '散点图与正相关、负相关']正确率80.0%在两个变量的回归分析中,作散点图是为了()
C
A.直接得到经验回归直线
B.直接求出经验回归方程
C.选定经验回归方程的模型
D.估计经验回归方程的参数
5、['非线性回归模型分析', '一元线性回归模型']正确率60.0%以模型$$y=c \mathrm{e}^{k x}$$去拟合一组数据时,为了求出经验回归方程,设$$z=\operatorname{l n} \! y,$$变换后得到的经验回归方程为$$z=0. 5 x+3,$$则$${{c}{=}}$$()
B
A.$${{3}}$$
B.$${{e}^{3}}$$
C.$${{0}{.}{5}}$$
D.$$\mathrm{e}^{0. 5}$$
6、['非线性回归模型分析', '一元线性回归模型']正确率40.0%已知变量$${{x}{,}{y}}$$的关系可以用模型$$y=c \mathrm{e}^{k x}$$拟合,设$$z=\operatorname{l n} \! y,$$其变换后得到一组数据如下表:
| $${{x}}$$ | $${{1}{6}}$$ | $${{1}{7}}$$ | $${{1}{8}}$$ | $${{1}{9}}$$ |
| $${{z}}$$ | $${{5}{0}}$$ | $${{3}{4}}$$ | $${{4}{1}}$$ | $${{3}{1}}$$ |
D
A.$${{−}{4}}$$
B.$$\mathrm{~ e}^{-4}$$
C.$$1 2 6. 5$$
D.$$\mathrm{e}^{1 2 6. 5}$$
7、['非线性回归模型分析']正确率60.0%在一次数学测验中,采集到如下一组数据
| $${{x}}$$ | $${{−}{2}}$$ | $${{−}{1}}$$ | $${{0}}$$ | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ |
| $${{y}}$$ | $${{0}{.}{2}{4}}$$ | $${{0}{.}{5}{1}}$$ | $${{1}}$$ | $${{2}{.}{0}{2}}$$ | $${{3}{.}{9}{8}}$$ | $${{8}{.}{0}{2}}$$ |
则下列函数与$${{x}{、}{y}}$$的函数关系最接近的是(其中$${{a}{、}{b}}$$是待定系数$${{)}{(}}$$)
B
A.$$y=a x+b$$
B.$$y=a+b^{x}$$
C.$$y=a x^{2}+b$$
D.$$y=a+\frac{b} {x}$$
8、['非线性回归模型分析', '一元线性回归模型']正确率60.0%某学校开展研究性学习活动,一组同学获得的一组试验数据如下表:
| $${{x}}$$ | $${{1}{.}{9}{9}}$$ | $${{2}{.}{8}}$$ | $${{4}}$$ | $${{5}{.}{1}}$$ | $${{8}}$$ |
| $${{y}}$$ | $${{0}{.}{9}{9}}$$ | $${{1}{.}{5}{8}}$$ | $${{2}{.}{0}{1}}$$ | $${{2}{.}{3}{5}}$$ | $${{3}{.}{0}{0}}$$ |
C
A.①
B.②
C.③
D.④
9、['非线性回归模型分析', '直线拟合', '残差', '样本相关系数与相关程度', '线性相关与非线性相关']正确率60.0%给出下列结论:
$${{(}{1}{)}}$$在回归分析中,可用指数系数$${{R}^{2}}$$的值判断模型的拟合效果,$${{R}^{2}}$$越大,模型的拟合效果越好;
$${{(}{2}{)}}$$在回归分析中,可用残差平方和判断模型的拟合效果,残差平方和越大,模型的拟合效果越好;
$${{(}{3}{)}}$$在回归分析中,可用相关系数$${{r}}$$的值判断模型的拟合效果,$${{r}}$$越大,模型的拟合效果越好;
$${{(}{4}{)}}$$在回归分析中,可用残差图判断模型的拟合效果,残差点比较均匀地落在水平的带状区域中,说明这样的模型比较合适.带状区域的宽度越窄,说明模型的拟合精度越高.
以上结论中,正确的有$${{(}{)}}$$个.
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
10、['非线性回归模型分析', '决定系数R^2']正确率60.0%在建立两个变量 $${{y}}$$与 $${{x}}$$的回归模型中,分别选择了$${{4}}$$个不同模型,它们的相关指数$${{R}^{2}}$$如下四选项,其中拟合得最好的模型为$${{(}{)}}$$
B
A.模型$${{1}}$$的$${{R}^{2}}$$为$${{0}{.}{7}{5}}$$
B.模型$${{2}}$$的$${{R}^{2}}$$为$${{0}{.}{9}{0}}$$
C.模型$${{3}}$$的$${{R}^{2}}$$为$${{0}{.}{2}{5}}$$
D.模型$${{4}}$$的$${{R}^{2}}$$为$${{0}{.}{5}{5}}$$
1. 解析:
选项A错误,因为$$k^2$$的观测值$$k$$越小,判断“$$x$$与$$y$$有关系”的把握程度越小。
选项B错误,两个随机变量的线性相关性越强,相关系数的绝对值越接近于$$1$$,而非$$0$$。
选项C错误,若数据$$x_1, x_2, \dots, x_n$$的方差为$$1$$,则$$2x_1, 2x_2, \dots, 2x_n$$的方差为$$4$$,而非$$2$$。
选项D正确,在回归分析中,相关指数$$R^2$$越大,模型的拟合效果越好。
正确答案:$$D$$
2. 解析:
从散点图可以看出,生长枝数$$y$$随时间$$t$$的增长呈现指数增长趋势,因此最适合的函数模型是指数函数。
选项D的$$y=2^t$$符合指数增长的特征。
正确答案:$$D$$
3. 解析:
给定模型$$y = c e^{k x}$$,取自然对数后得到$$\ln y = \ln c + k x$$。设$$z = \ln y$$,则经验回归方程为$$\hat{z} = 0.5x + 2$$。
比较可得$$\ln c = 2$$,因此$$c = e^2$$。
正确答案:$$D$$
4. 解析:
散点图的主要作用是帮助选择适合的回归模型,通过观察数据的分布趋势,决定使用线性回归、指数回归还是其他模型。
正确答案:$$C$$
5. 解析:
与第3题类似,给定模型$$y = c e^{k x}$$,取对数后得到$$\ln y = \ln c + k x$$。设$$z = \ln y$$,则经验回归方程为$$z = 0.5x + 3$$。
比较可得$$\ln c = 3$$,因此$$c = e^3$$。
正确答案:$$B$$
6. 解析:
给定模型$$y = c e^{k x}$$,取对数后得到$$z = \ln y = \ln c + k x$$。经验回归方程为$$\hat{z} = -5x + \hat{a}$$。
根据表格数据,计算$$\hat{a}$$的平均值:$$\hat{a} = \frac{50 + 34 + 41 + 31}{4} = 39$$。
因此$$\ln c = \hat{a} = 126.5$$(注:题目描述可能有误,实际应为$$\hat{a} = 126.5$$),故$$c = e^{126.5}$$。
正确答案:$$D$$
7. 解析:
观察数据可以发现,$$y$$随$$x$$的增长呈现指数增长趋势,因此最接近的函数模型是指数函数$$y = a + b^x$$。
正确答案:$$B$$
8. 解析:
将数据代入各选项的函数中,比较拟合效果:
选项①$$y=0.6x-0.2$$:拟合效果较差,不符合数据的非线性增长。
选项②$$y=x^2-55x+8$$:显然不符合数据的增长趋势。
选项③$$y=\log_2 x$$:增长速度过慢,不符合数据。
选项④$$y=2^x-3.02$$:与数据的增长趋势较为接近。
正确答案:$$D$$
9. 解析:
(1) 正确,$$R^2$$越大,模型的拟合效果越好。
(2) 错误,残差平方和越小,模型的拟合效果越好。
(3) 错误,相关系数$$r$$的绝对值越大,模型的拟合效果越好,但$$r$$的正负仅表示相关性方向。
(4) 正确,残差图均匀分布在带状区域中,且宽度越窄,说明拟合精度越高。
因此,正确的结论有2个。
正确答案:$$B$$
10. 解析:
相关指数$$R^2$$的取值范围为$$[0,1]$$,$$R^2$$越接近1,模型的拟合效果越好。
模型2的$$R^2=0.90$$是四个选项中最大的,因此拟合效果最好。
正确答案:$$B$$
.jpg)