正确率60.0%在复平面内,复数 $${{6}{+}{5}{i}}$$ 与 $$- 3+4 \mathrm{i}$$ 对应的向量分别为$$\overrightarrow{O A}$$与$$\overrightarrow{O B},$$则向量$$\overrightarrow{A B}$$对应的复数是()
C
A.$$- 1+9 \mathrm{i}$$
B.$${{9}{+}{i}}$$
C.$${{−}{9}{−}{i}}$$
D.$${{9}{−}{i}}$$
2、['复平面内的点、复数及平面向量']正确率60.0%如图,在复平面内,正方形$${{O}{A}{C}{B}}$$的顶点$$A, ~ B, ~ O$$分别对应复数$$1+2 \mathrm{i}, ~-2+\mathrm{i}, ~ 0,$$则正方形的顶点$${{C}}$$对应的复数为()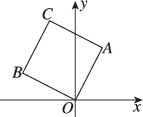
D
A.$${{3}{+}{i}}$$
B.$${{3}{−}{i}}$$
C.$${{1}{−}{3}{i}}$$
D.$$- 1+3 \mathrm{i}$$
3、['复平面内的点、复数及平面向量', '共轭复数']正确率80.0%已知$$z ( 1+i )=2+i$$,则在复平面内复数对应的点位于$${{(}{)}}$$
A
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4、['复平面内的点、复数及平面向量', '复数的四则运算综合应用']正确率60.0%已知复数$${{z}_{1}{,}{{z}_{2}}}$$在复平面内对应的点关于直线$${{y}{=}{x}}$$对称,$$z_{1}=1+2 i$$,则$$\frac{z_{1}} {z_{2}}=($$)
D
A.$$\frac{3} {5}-\frac{4} {5} i$$
B.$$\frac{3} {5}+\frac{4} {5} i$$
C.$$\frac{4} {5}-\frac{3} {5} i$$
D.$$\frac{4} {5}+\frac{3} {5} i$$
5、['复平面内的点、复数及平面向量', '复数的模']正确率60.0%如图所示,在复平面内,网格中的每个小正方形的边长都为$${{1}{,}}$$点$${{A}{,}{B}}$$对应的复数分别是$$z_{1}, ~ z_{2},$$则$$| z_{1}-z_{2} |=$$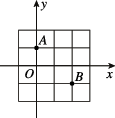 ()
()
A
A.$${{2}{\sqrt {2}}}$$
B.$${{1}{+}{\sqrt {5}}}$$
C.$${{2}}$$
D.$${\sqrt {5}}$$
6、['复平面内的点、复数及平面向量', '复数的乘法', '复数的除法', '复数的四则运算综合应用']正确率60.0%复数$$z_{1}=( \frac{1-i} {1+i} )^{2}, \, \, z_{2}=2-i^{3}$$分别对应复平面上的点$${{P}{、}{Q}}$$,则向量$$\overrightarrow{P Q}$$对应的复数是()
D
A.$${\sqrt {{1}{0}}}$$
B.$${{−}{3}{−}{i}}$$
C.$${{1}{+}{i}}$$
D.$${{3}{+}{i}}$$
7、['复平面内的点、复数及平面向量', '复数的减法及其几何意义']正确率60.0%复数$$z=m ( 3+\mathrm{i} )-( 2+\mathrm{i} ) ( m \in{\bf R},$$为虚数单位)在复平面内对应的点不可能位于()
B
A.第一象限
B.第二象限
C.第三象限
D.第四象限
8、['复平面内的点、复数及平面向量', '复数的模', '复数的有关概念', '共轭复数', '复数的四则运算综合应用']正确率60.0%若复数$${{z}}$$满足$$( 3+4 i ) \enspace z=5$$,则下列说法不正确的是()
A
A.复数$${{z}}$$的虚部为$$- \frac{4} {5} i$$
B.复数$$z-\overline{{z}}$$为纯虚数
C.复数$${{z}}$$在复平面内对应的点位于第四象限
D.复数$${{z}}$$的模为$${{1}}$$
9、['复平面内的点、复数及平面向量', '共轭复数']正确率60.0%在复平面内,复数$${{z}}$$的对应点为$$( 1, \ 2 )$$,复数$${{z}}$$的共轭复数为()
B
A.$${{1}{+}{2}{i}}$$
B.$${{1}{−}{2}{i}}$$
C.$${{−}{2}{+}{i}}$$
D.$${{−}{2}{−}{i}}$$
10、['复平面内的点、复数及平面向量', '复数的除法']正确率60.0%复数$$\frac{2 i} {1-i}$$在复平面内对应的点为$${{(}{)}}$$
B
A.$$(-1,-1 )$$
B.$$(-1, 1 )$$
C.$$( 1,-1 )$$
D.$$\left( 1, 1 \right)$$
1. 解析:
向量 $$\overrightarrow{AB}$$ 对应的复数等于终点 $$B$$ 对应的复数减去起点 $$A$$ 对应的复数。因此:
$$ \overrightarrow{AB} = (-3 + 4i) - (6 + 5i) = -9 - i $$
正确答案是 $$C$$。
2. 解析:
正方形 $$OACB$$ 中,点 $$C$$ 的坐标等于点 $$A$$ 和点 $$B$$ 的向量和,因为 $$O$$ 是原点。因此:
$$ C = (1 + 2i) + (-2 + i) = -1 + 3i $$
正确答案是 $$D$$。
3. 解析:
首先解方程 $$z(1+i) = 2 + i$$ 得:
$$ z = \frac{2 + i}{1 + i} = \frac{(2 + i)(1 - i)}{(1 + i)(1 - i)} = \frac{3 - i}{2} = \frac{3}{2} - \frac{1}{2}i $$
复平面内对应的点为 $$(\frac{3}{2}, -\frac{1}{2})$$,位于第四象限。
正确答案是 $$D$$。
4. 解析:
复数 $$z_1 = 1 + 2i$$ 对应的点为 $$(1, 2)$$,其关于直线 $$y = x$$ 对称的点为 $$(2, 1)$$,因此 $$z_2 = 2 + i$$。
计算 $$\frac{z_1}{z_2} = \frac{1 + 2i}{2 + i} = \frac{(1 + 2i)(2 - i)}{(2 + i)(2 - i)} = \frac{4 + 3i}{5} = \frac{4}{5} + \frac{3}{5}i $$
正确答案是 $$D$$。
5. 解析:
根据图中网格,假设点 $$A$$ 在 $$(1, 1)$$,点 $$B$$ 在 $$(3, 2)$$,则:
$$ z_1 = 1 + i $$,$$ z_2 = 3 + 2i $$
$$ |z_1 - z_2| = |(1 + i) - (3 + 2i)| = |-2 - i| = \sqrt{(-2)^2 + (-1)^2} = \sqrt{5} $$
正确答案是 $$D$$。
6. 解析:
计算 $$z_1 = \left(\frac{1 - i}{1 + i}\right)^2 = \left(\frac{(1 - i)^2}{(1 + i)(1 - i)}\right) = \left(\frac{-2i}{2}\right)^2 = (-i)^2 = -1 $$
计算 $$z_2 = 2 - i^3 = 2 - (-i) = 2 + i $$
向量 $$\overrightarrow{PQ}$$ 对应的复数为 $$z_2 - z_1 = (2 + i) - (-1) = 3 + i $$
正确答案是 $$D$$。
7. 解析:
化简复数 $$z = m(3 + i) - (2 + i) = (3m - 2) + (m - 1)i $$
复平面内对应的点为 $$(3m - 2, m - 1)$$。
若点位于第二象限,需满足 $$3m - 2 < 0$$ 且 $$m - 1 > 0$$,即 $$m < \frac{2}{3}$$ 且 $$m > 1$$,无解。因此不可能位于第二象限。
正确答案是 $$B$$。
8. 解析:
解方程 $$(3 + 4i)z = 5$$ 得:
$$ z = \frac{5}{3 + 4i} = \frac{5(3 - 4i)}{(3 + 4i)(3 - 4i)} = \frac{15 - 20i}{25} = \frac{3}{5} - \frac{4}{5}i $$
选项 $$A$$ 错误,因为虚部是 $$-\frac{4}{5}$$,不是 $$-\frac{4}{5}i$$。
选项 $$B$$ 正确,因为 $$z - \overline{z} = -\frac{8}{5}i$$ 是纯虚数。
选项 $$C$$ 正确,因为点 $$(\frac{3}{5}, -\frac{4}{5})$$ 在第四象限。
选项 $$D$$ 正确,因为 $$|z| = \sqrt{(\frac{3}{5})^2 + (-\frac{4}{5})^2} = 1 $$。
正确答案是 $$A$$。
9. 解析:
复数 $$z$$ 对应点为 $$(1, 2)$$,因此 $$z = 1 + 2i$$,其共轭复数为 $$1 - 2i$$。
正确答案是 $$B$$。
10. 解析:
计算复数 $$\frac{2i}{1 - i} = \frac{2i(1 + i)}{(1 - i)(1 + i)} = \frac{2i - 2}{2} = -1 + i $$
复平面内对应的点为 $$(-1, 1)$$。
正确答案是 $$B$$。
.jpg)