.jpg)
正确率60.0%设$${{i}}$$为虚数单位，复数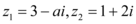
，若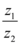
是纯虚数，则实数$${{a}}$$
C
A.$${{−}{6}}$$
B.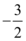
C.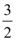
D.$${{6}}$$
首先，给定复数 $$z = \frac{2 + ai}{1 + i}$$，其中 $$i$$ 为虚数单位，$$a$$ 为实数。题目要求 $$z$$ 是纯虚数，即其实部为 0 且虚部不为 0。
步骤 1：化简复数 $$z$$
将分子和分母同时乘以 $$1 - i$$（分母的共轭复数），以消除分母中的虚数部分：
$$ z = \frac{(2 + ai)(1 - i)}{(1 + i)(1 - i)} $$
步骤 2：计算分子和分母
展开分子：
$$ (2 + ai)(1 - i) = 2 \cdot 1 + 2 \cdot (-i) + ai \cdot 1 + ai \cdot (-i) = 2 - 2i + ai - ai^2 $$
由于 $$i^2 = -1$$，代入得：
$$ 2 - 2i + ai + a = (2 + a) + (a - 2)i $$
计算分母：
$$ (1 + i)(1 - i) = 1^2 - i^2 = 1 - (-1) = 2 $$
因此，$$z$$ 化简为：
$$ z = \frac{(2 + a) + (a - 2)i}{2} = \frac{2 + a}{2} + \frac{a - 2}{2}i $$
步骤 3：纯虚数条件
纯虚数的实部为 0 且虚部不为 0，因此：
$$ \frac{2 + a}{2} = 0 \quad \text{且} \quad \frac{a - 2}{2} \neq 0 $$
解得：
$$ 2 + a = 0 \quad \Rightarrow \quad a = -2 $$
验证虚部不为 0：
$$ \frac{-2 - 2}{2} = -2 \neq 0 $$
因此，实数 $$a$$ 的值为 $$-2$$。
最终答案
选项 B 正确，答案为 $$-2$$。