正确率40.0%如图,在$${{Δ}{A}{B}{C}}$$中,$$\vec{A D}=\frac{2} {3} \vec{A C}, \; \; \vec{B P}=\frac{1} {3} \vec{B D}$$,若$$\vec{A P}=\lambda\vec{A} B+\mu\vec{A C},$$则$$\frac{\lambda} {\mu}$$的值为$${{(}{)}}$$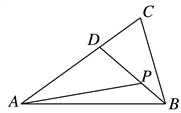
D
A.$${{−}{3}}$$
B.$${{−}{2}}$$
C.$${{2}}$$
D.$${{3}}$$
2、['空间直角坐标系中两点之间的距离公式', '复数的加法及其几何意义', '复数的减法及其几何意义']正确率60.0%在复平面内,复数$$7-4 i, \; 2+8 i$$对应的向量分别是$$\overrightarrow{O A}$$和$$\overrightarrow{O B},$$其中$${{O}}$$是原点,则$$| A B |=\c($$)
D
A.$${\sqrt {{9}{7}}}$$
B.$${{1}{8}}$$
C.$${{1}{2}}$$
D.$${{1}{3}}$$
3、['复数的模', '复数的减法及其几何意义', '与圆有关的最值问题']正确率40.0%若$${{i}}$$为虚数单位,复数$${{z}}$$满足$$| z | \leq1$$,则$$| z-2 \mathrm{i} |$$的最大值为()
B
A.$${{2}}$$
B.$${{3}}$$
C.$${{2}{\sqrt {3}}}$$
D.$${{3}{\sqrt {3}}}$$
4、['复平面内的点、复数及平面向量', '复数的减法及其几何意义']正确率80.0%已知$${{i}}$$是虚数单位,复数$${{z}}$$满足$$z+3 \mathrm{i}=1+\mathrm{i},$$则$${{z}}$$在复平面内对应的点位于()
D
A.第一象限
B.第二象限
C.第三象限
D.第四象限
5、['复数的有关概念', '共轭复数', '复数的减法及其几何意义']正确率60.0%已知复数$${{z}}$$满足$$z-\overline{{z}}=2 \mathrm{i}$$,则$${{z}}$$的虚部是()
B
A.$${{−}{1}}$$
B.$${{1}}$$
C.$${{−}{i}}$$
D.$${{i}}$$
6、['复数的模', '复数的减法及其几何意义']正确率60.0%已知复数$$z_{1}=1+\mathrm{i}, \; \; z_{2}=1+3 \mathrm{i},$$则$$\left| z_{2}-z_{1} \right|=$$()
C
A.$${\sqrt {2}}$$
B.$${\sqrt {{1}{0}}}$$
C.$${{2}}$$
D.$${{4}}$$
7、['共轭复数', '复数的加法及其几何意义', '复数的减法及其几何意义', '复数的四则运算综合应用']正确率60.0%已知$${{i}}$$是虚数单位,$$z=i ( 2-i )+i^{3}$$的共轭复数为则
对应复平面内的点在 ()
D
A.第一象限
B.第二象限
C.第三象限
D.第四象限
8、['复平面内的点、复数及平面向量', '复数的加法及其几何意义', '复数的减法及其几何意义']正确率60.0%在复平面内,$$\overrightarrow{A B}, \ \overrightarrow{A C}$$对应的复数分别为$$- 1+2 i, ~-2-3 i$$,则$$\overrightarrow{B C}$$对应的复数为()
A
A.$$- 1-5 i$$
B.$$- 1+5 i$$
C.$${{3}{−}{4}{i}}$$
D.$${{3}{+}{4}{i}}$$
9、['复数的模', '复数的加法及其几何意义', '复数的减法及其几何意义']正确率60.0%已知复数$${{z}}$$满足$$3-z=1-\mathrm{i} ( \mathrm{i}$$为虚数单位$${{)}}$$,则复数$${{z}}$$的模为()
D
A.$${{2}}$$
B.
C.$${{5}}$$
D.
正确率19.999999999999996%若复数$${{z}_{1}{,}{{z}_{2}}}$$满足$$| z_{1} |=| z_{2} |=1$$,$$z_{1}-z_{2}=\frac{2-4 \mathrm{i}} {2+\mathrm{i}},$$则$$z_{1} \cdot z_{2}=$$()
A
A.$${{1}}$$
B.$${{−}{1}}$$
C.$${{i}}$$
D.$${{−}{i}}$$
1. 解析:
根据题意,$$ \vec{AD} = \frac{2}{3} \vec{AC} $$,所以 $$ \vec{DC} = \frac{1}{3} \vec{AC} $$。
又 $$ \vec{BP} = \frac{1}{3} \vec{BD} $$,可以表示为 $$ \vec{P} = \vec{B} + \frac{1}{3} (\vec{D} - \vec{B}) = \frac{2}{3} \vec{B} + \frac{1}{3} \vec{D} $$。
由于 $$ \vec{D} = \vec{A} + \frac{2}{3} \vec{AC} $$,代入得:
$$ \vec{P} = \frac{2}{3} \vec{B} + \frac{1}{3} \left( \vec{A} + \frac{2}{3} \vec{AC} \right) = \frac{1}{3} \vec{A} + \frac{2}{3} \vec{B} + \frac{2}{9} \vec{AC} $$。
而 $$ \vec{AP} = \vec{P} - \vec{A} = \frac{2}{3} \vec{AB} + \frac{2}{9} \vec{AC} $$。
与题目给出的 $$ \vec{AP} = \lambda \vec{AB} + \mu \vec{AC} $$ 对比,可得 $$ \lambda = \frac{2}{3} $$,$$ \mu = \frac{2}{9} $$。
因此 $$ \frac{\lambda}{\mu} = 3 $$,答案为 D。
2. 解析:
复数 $$ 7-4i $$ 对应的向量为 $$ \overrightarrow{OA} = (7, -4) $$,复数 $$ 2+8i $$ 对应的向量为 $$ \overrightarrow{OB} = (2, 8) $$。
向量 $$ \overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} = (2-7, 8-(-4)) = (-5, 12) $$。
其模长为 $$ |AB| = \sqrt{(-5)^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 $$。
答案为 D。
3. 解析:
复数 $$ z $$ 满足 $$ |z| \leq 1 $$,表示 $$ z $$ 在复平面上位于单位圆内或圆上。
$$ |z - 2i| $$ 表示 $$ z $$ 到点 $$ 2i $$ 的距离,其最大值为单位圆的半径加上 $$ 2i $$ 到原点的距离,即 $$ 1 + 2 = 3 $$。
答案为 B。
4. 解析:
由 $$ z + 3i = 1 + i $$,解得 $$ z = 1 + i - 3i = 1 - 2i $$。
复数 $$ z = 1 - 2i $$ 对应的点为 $$ (1, -2) $$,位于第四象限。
答案为 D。
5. 解析:
设 $$ z = a + bi $$,则 $$ \overline{z} = a - bi $$。
由题意 $$ z - \overline{z} = 2i $$,即 $$ (a + bi) - (a - bi) = 2bi = 2i $$,解得 $$ b = 1 $$。
因此 $$ z $$ 的虚部为 1,答案为 B。
6. 解析:
$$ z_2 - z_1 = (1 + 3i) - (1 + i) = 2i $$。
其模长为 $$ |2i| = 2 $$。
答案为 C。
7. 解析:
计算 $$ z = i(2 - i) + i^3 = 2i - i^2 + i^3 = 2i + 1 - i = 1 + i $$。
其共轭复数为 $$ \overline{z} = 1 - i $$。
复数 $$ 1 - i $$ 对应的点为 $$ (1, -1) $$,位于第四象限。
答案为 D。
8. 解析:
$$ \overrightarrow{AB} $$ 对应的复数为 $$ -1 + 2i $$,$$ \overrightarrow{AC} $$ 对应的复数为 $$ -2 - 3i $$。
$$ \overrightarrow{BC} = \overrightarrow{AC} - \overrightarrow{AB} = (-2 - 3i) - (-1 + 2i) = -1 - 5i $$。
答案为 A。
9. 解析:
由 $$ 3 - z = 1 - i $$,解得 $$ z = 2 + i $$。
其模长为 $$ |z| = \sqrt{2^2 + 1^2} = \sqrt{5} $$。
答案为 D。
10. 解析:
由 $$ z_1 - z_2 = \frac{2 - 4i}{2 + i} $$,化简分母有理化:
$$ \frac{2 - 4i}{2 + i} \cdot \frac{2 - i}{2 - i} = \frac{(2 - 4i)(2 - i)}{4 + 1} = \frac{4 - 2i - 8i + 4i^2}{5} = \frac{4 - 10i - 4}{5} = \frac{-10i}{5} = -2i $$。
因此 $$ z_1 - z_2 = -2i $$。
又 $$ |z_1| = |z_2| = 1 $$,设 $$ z_1 = e^{i\theta_1} $$,$$ z_2 = e^{i\theta_2} $$,则 $$ |z_1 - z_2| = 2 $$,即 $$ |e^{i\theta_1} - e^{i\theta_2}| = 2 $$。
解得 $$ \theta_1 - \theta_2 = \pi $$,即 $$ z_1 = -z_2 $$。
因此 $$ z_1 \cdot z_2 = -z_2 \cdot z_2 = -|z_2|^2 = -1 $$。
答案为 B。
.jpg)