.jpg)
正确率60.0%已知$$a \in\mathbf{R}， \mathrm{~ i ~}$$为虚数单位，若$$\frac{a-\mathrm{i}} {3+\mathrm{i}}$$为实数，则$${{a}{=}}$$（）
A
A.$${{−}{3}}$$
B.$$\frac{1} {3}$$
C.$${{3}}$$
D.$$- \frac{1} {3}$$
2、['复数的除法']正确率80.0%已知复数$${{z}}$$满足$$( 1-\mathrm{i} ) z=2，$$则$${{z}{=}}$$（）
D
A.$${{−}{1}{−}{i}}$$
B.$${{−}{1}{+}{i}}$$
C.$${{1}{−}{i}}$$
D.$${{1}{+}{i}}$$
3、['共轭复数'， '复数的除法']正确率60.0%复数$$z=\frac{-3+\mathrm{i}} {2+\mathrm{i}}$$的共轭复数是（）
D
A.$${{2}{+}{i}}$$
B.$${{2}{−}{i}}$$
C.$${{−}{1}{+}{i}}$$
D.$${{−}{1}{−}{i}}$$
4、['共轭复数'， '复数的乘法'， '复数的除法']正确率60.0%已知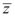
为复数
的共轭复数，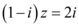
，则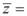
$${{(}{)}}$$
B
A.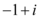
B.
C.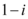
D.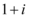
正确率60.0%若复数$$\frac{a+2 i} {1-i}$$在复平面内所对应的点在实轴上，则实数$${{a}{=}{（}}$$）
B
A.$${{2}}$$
B.$${{−}{2}}$$
C.$${{1}}$$
D.$${{0}}$$
6、['复数的除法'， '复数的四则运算综合应用']正确率60.0%已知$${{i}}$$是虚数单位，复数$$\frac{5} {2-i}-i=( \textit{} )$$
B
A.$${{−}{2}}$$
B.$${{2}}$$
C.$${{i}{−}{2}}$$
D.$${{2}{+}{i}}$$
7、['复数的有关概念'， '复数的除法']正确率60.0%复数$${{z}}$$满足$$\bar{z} ( 1+i )=2 i ( i$$为虚数单位$${{)}}$$，则复数$${{z}{=}{（}}$$）
A
A.$${{1}{−}{i}}$$
B.$${{1}{+}{2}{i}}$$
C.$${{1}{+}{i}}$$
D.$${{2}{−}{2}{i}}$$
8、['复平面内的点、复数及平面向量'， '复数的除法']正确率60.0%已知复数$${{z}}$$满足$$( 1+i ) z=-1+i$$，则在复平面内，$${{z}}$$对应的点$${{Z}}$$的坐标为（）
A
A.$$( 0， 1 )$$
B.$$( 0，-1 )$$
C.$$( 1， 0 )$$
D.$$(-1， 0 )$$
9、['复数的有关概念'， '复数的除法']正确率60.0%已知$${{a}{∈}{R}}$$，复数$$z=\frac{a-2 i} {3+i} ( i$$为虚数单位$${）}$$，若$${{z}}$$为纯虚数，则$${{a}{=}{（}}$$）
A
A.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
B.$$- \frac2 3$$
C.$${{6}}$$
D.$${{−}{6}}$$
10、['共轭复数'， '复数的乘法'， '复数的除法']正确率60.0%设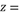
，
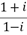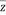是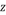
的共轭复数，则
$${{(}{)}}$$
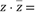C
A.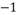
B.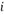
C.$${{1}}$$
D.$${{4}}$$
1. 要使 $$\frac{a-\mathrm{i}}{3+\mathrm{i}}$$ 为实数，其虚部必须为零。先进行分母有理化：
$$\frac{a-\mathrm{i}}{3+\mathrm{i}} \cdot \frac{3-\mathrm{i}}{3-\mathrm{i}} = \frac{(3a -1) + (-a -3)\mathrm{i}}{10}$$
令虚部为零，即 $$-a -3 = 0$$，解得 $$a = -3$$。答案为 A。
2. 解方程 $$(1-\mathrm{i})z = 2$$，得 $$z = \frac{2}{1-\mathrm{i}}$$。有理化分母：
$$z = \frac{2(1+\mathrm{i})}{(1-\mathrm{i})(1+\mathrm{i})} = \frac{2(1+\mathrm{i})}{2} = 1+\mathrm{i}$$。答案为 D。
3. 计算复数 $$z = \frac{-3+\mathrm{i}}{2+\mathrm{i}}$$ 的共轭复数。先有理化：
$$z = \frac{(-3+\mathrm{i})(2-\mathrm{i})}{(2+\mathrm{i})(2-\mathrm{i})} = \frac{-5 +5\mathrm{i}}{5} = -1 + \mathrm{i}$$
其共轭复数为 $$-1 - \mathrm{i}$$。答案为 D。
4. 设复数 $$z = x + y\mathrm{i}$$，则其共轭复数为 $$\overline{z} = x - y\mathrm{i}$$。根据题意：
$$(x - y\mathrm{i})(1 + \mathrm{i}) = 2\mathrm{i}$$
展开得 $$(x + y) + (x - y)\mathrm{i} = 2\mathrm{i}$$，解得 $$x + y = 0$$ 且 $$x - y = 2$$，即 $$x = 1$$，$$y = -1$$。
因此 $$z = 1 - \mathrm{i}$$，其共轭复数为 $$1 + \mathrm{i}$$。答案为 C。
5. 复数 $$\frac{a+2\mathrm{i}}{1-\mathrm{i}}$$ 在实轴上，说明其虚部为零。有理化分母：
$$\frac{(a+2\mathrm{i})(1+\mathrm{i})}{(1-\mathrm{i})(1+\mathrm{i})} = \frac{(a-2) + (a+2)\mathrm{i}}{2}$$
令虚部为零，即 $$a + 2 = 0$$，解得 $$a = -2$$。答案为 B。
6. 计算 $$\frac{5}{2-\mathrm{i}} - \mathrm{i}$$。先有理化：
$$\frac{5(2+\mathrm{i})}{(2-\mathrm{i})(2+\mathrm{i})} - \mathrm{i} = \frac{10 + 5\mathrm{i}}{5} - \mathrm{i} = 2 + \mathrm{i} - \mathrm{i} = 2$$。答案为 B。
7. 设复数 $$z = x + y\mathrm{i}$$，则其共轭复数为 $$\overline{z} = x - y\mathrm{i}$$。根据题意：
$$(x - y\mathrm{i})(1 + \mathrm{i}) = 2\mathrm{i}$$
展开得 $$(x + y) + (x - y)\mathrm{i} = 2\mathrm{i}$$，解得 $$x + y = 0$$ 且 $$x - y = 2$$，即 $$x = 1$$，$$y = -1$$。
因此 $$z = 1 - \mathrm{i}$$。答案为 A。
8. 解方程 $$(1+\mathrm{i})z = -1 + \mathrm{i}$$，得 $$z = \frac{-1 + \mathrm{i}}{1 + \mathrm{i}}$$。有理化分母：
$$z = \frac{(-1 + \mathrm{i})(1 - \mathrm{i})}{(1 + \mathrm{i})(1 - \mathrm{i})} = \frac{2\mathrm{i}}{2} = \mathrm{i}$$
因此 $$z$$ 对应的点为 $$(0, 1)$$。答案为 A。
9. 复数 $$z = \frac{a - 2\mathrm{i}}{3 + \mathrm{i}}$$ 为纯虚数，其实部为零。有理化分母：
$$z = \frac{(a - 2\mathrm{i})(3 - \mathrm{i})}{(3 + \mathrm{i})(3 - \mathrm{i})} = \frac{(3a - 2) + (-a -6)\mathrm{i}}{10}$$
令实部为零，即 $$3a - 2 = 0$$，解得 $$a = \frac{2}{3}$$。答案为 A。
10. 设复数 $$z = 1 + \mathrm{i}$$，则其共轭复数为 $$\overline{z} = 1 - \mathrm{i}$$。计算 $$z \cdot \overline{z}$$：
$$(1 + \mathrm{i})(1 - \mathrm{i}) = 1 - \mathrm{i}^2 = 2$$。答案为 D。