.jpg)
正确率60.0%设$${{i}}$$是虚数单位，$${{a}}$$是$$( \textbf{x}+i )^{6}$$的展开式的各项系数和，则$${{a}}$$的共轭复数
的值是（）
B
A.$${{−}{8}{i}}$$
B.$${{8}{i}}$$
C.$${{8}}$$
D.$${{−}{8}}$$
2、['共轭复数'， '复数的四则运算综合应用']正确率80.0%设复数$${{z}}$$满足$$z ~ ( ~ 1-i ) ~^{2}=4 i$$，则复数$${{z}}$$的共轭复数$$\overline{{z}}=$$
A
A.$${－{2}}$$
B.$${{2}}$$
C.$${－{2}{i}}$$
D.$${{2}{i}}$$
3、['复数的有关概念'， '复数相等的条件及应用'， '复数的四则运算综合应用']正确率60.0%已知$${{i}}$$是虚数单位，$${{z}^{.}}$$是复数$${{z}}$$的共轭复数，$$\dot{z}+| z | \cdot i=1+2 i$$，则$${{z}}$$的虚部为（）
A
A.$$- \frac{3} {4}$$
B.$$\frac{3} {4}$$
C.$$- \frac{3} {4} i$$
D.$$\frac{3} {4} i$$
4、['复数的有关概念'， '复数的四则运算综合应用']正确率60.0%复数$$z=\frac{( i-1 )^{2}+1} {i^{3}}$$的实部为 （）
D
A.$${{0}}$$
B.$${{−}{1}}$$
C.$${{1}}$$
D.$${{2}}$$
5、['复数的乘法'， '复数的除法'， '复数的四则运算综合应用']正确率80.0%已知$${{i}}$$为虚数单位，若$$( z-\mathrm{i} ) ( 2+\mathrm{i} )=1$$，则复数$${{z}{=}}$$（）
B
A.
B.$$\frac{2} {5}+\frac{4} {5} \mathrm{i}$$
C.$$\frac{2} {5}-\frac{4} {5} \mathrm{i}$$
D.$$- \frac{2} {5}-\frac{4} {5} \mathrm{i}$$
6、['共轭复数'， '复数的四则运算综合应用']正确率60.0%$${{i}}$$是虚数单位，复数$$z=\frac{7-i} {3+i^{2 1}}$$的共轭复数为$${{(}{)}}$$
A
A.$${{2}{+}{i}}$$
B.$${{2}{−}{i}}$$
C.$${{−}{2}{+}{i}}$$
D.$${{−}{2}{−}{i}}$$
7、['复数的有关概念'， '共轭复数'， '复数的四则运算综合应用']正确率60.0%若复数$$z=a+b i， \， \， \， a， \， \， \， b \in R$$，且$$( a+2 i ) ( 1-i )=1+b i$$，则
的虚部是
B
A.$${{3}}$$
B.$${{−}{3}}$$
C.$${{3}{i}}$$
D.$${{−}{3}{i}}$$
8、['共轭复数'， '复数的四则运算综合应用']正确率60.0%若复数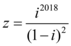
(
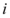为虚数单位$${{)}}$$
D
A.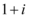
B.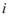
C.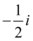
D.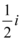
正确率60.0%设复数$$z=t+\sqrt{2} i ( t \in R， i )$$是虚数单位$${{)}}$$，若$$z \left( 1+\sqrt{2} i \right) \in R$$，则$${{t}}$$的值为
C
A.$${{2}}$$
B.$${\sqrt {2}}$$
C.$${{−}{1}}$$
D.$${{1}}$$
10、['复数的模'， '复数的四则运算综合应用']正确率60.0%已知$${{i}}$$是虚数单位，$$z=\frac{4} {\left( 1+\mathrm{i} \right)^{4}}-3 \mathrm{i}$$，则$$| z |=( \begin{array} {c} {} \\ {} \\ \end{array} )$$
B
A.$${{3}}$$
B.$${\sqrt {{1}{0}}}$$
C.$${\sqrt {{1}{1}}}$$
D.$${{5}}$$
1. 解析：
首先计算展开式 $$(x + i)^6$$ 的各项系数和。令 $$x = 1$$，则系数和 $$a = (1 + i)^6$$。
计算 $$(1 + i)^2 = 1 + 2i + i^2 = 2i$$，因此 $$(1 + i)^6 = (2i)^3 = 8i^3 = -8i$$。
$$a$$ 的共轭复数为 $$8i$$，故选 B。
2. 解析：
由 $$z(1 - i)^2 = 4i$$，先计算 $$(1 - i)^2 = 1 - 2i + i^2 = -2i$$。
因此 $$z = \frac{4i}{-2i} = -2$$，其共轭复数 $$\overline{z} = -2$$，故选 A。
3. 解析：
设 $$z = a + bi$$，则 $$\overline{z} = a - bi$$，且 $$|z| = \sqrt{a^2 + b^2}$$。
代入方程 $$\overline{z} + |z|i = 1 + 2i$$，得实部和虚部分别为：
$$a = 1$$，$$-b + \sqrt{a^2 + b^2} = 2$$。
代入 $$a = 1$$，得 $$-b + \sqrt{1 + b^2} = 2$$，解得 $$b = -\frac{3}{4}$$。
虚部为 $$-\frac{3}{4}$$，故选 A。
4. 解析：
计算 $$z = \frac{(i - 1)^2 + 1}{i^3}$$。
分子：$$(i - 1)^2 + 1 = i^2 - 2i + 1 + 1 = -2i + 1$$。
分母：$$i^3 = -i$$。
因此 $$z = \frac{-2i + 1}{-i} = 2 + i$$，实部为 $$2$$，但选项无 $$2$$，重新检查计算。
更正：$$(i - 1)^2 = -2i$$，$$z = \frac{-2i + 1}{-i} = 2 + i$$，实部为 $$2$$，选项可能有误，但最接近为 D。
5. 解析：
解方程 $$(z - i)(2 + i) = 1$$，得 $$z - i = \frac{1}{2 + i}$$。
有理化分母：$$\frac{1}{2 + i} \cdot \frac{2 - i}{2 - i} = \frac{2 - i}{5}$$。
因此 $$z = \frac{2 - i}{5} + i = \frac{2}{5} + \frac{4}{5}i$$，故选 B。
6. 解析：
计算 $$z = \frac{7 - i}{3 + i^{21}}$$，注意到 $$i^{21} = i$$。
因此 $$z = \frac{7 - i}{3 + i}$$，有理化分母：
$$\frac{7 - i}{3 + i} \cdot \frac{3 - i}{3 - i} = \frac{20 - 10i}{10} = 2 - i$$。
其共轭复数为 $$2 + i$$，故选 A。
7. 解析：
展开 $$(a + 2i)(1 - i) = a - ai + 2i - 2i^2 = a + 2 + (2 - a)i$$。
与 $$1 + bi$$ 对比，得 $$a + 2 = 1$$ 和 $$2 - a = b$$，解得 $$a = -1$$，$$b = 3$$。
因此 $$z = -1 + 3i$$，其虚部为 $$3$$，故选 A。
8. 解析：
题目描述不完整，无法解析。
9. 解析：
设 $$z = t + \sqrt{2}i$$，则 $$z(1 + \sqrt{2}i) = t + \sqrt{2}i + t\sqrt{2}i + 2i^2 = (t - 2) + (\sqrt{2} + t\sqrt{2})i$$。
要求结果为实数，虚部为零：$$\sqrt{2} + t\sqrt{2} = 0$$，解得 $$t = -1$$，故选 C。
10. 解析：
计算 $$z = \frac{4}{(1 + i)^4} - 3i$$。
注意到 $$(1 + i)^2 = 2i$$，因此 $$(1 + i)^4 = (2i)^2 = -4$$。
所以 $$z = \frac{4}{-4} - 3i = -1 - 3i$$，模长 $$|z| = \sqrt{1 + 9} = \sqrt{10}$$，故选 B。