正确率40.0%某种疾病可分为两种类型:第一类占$${{7}{0}{%}{,}}$$可由药物$${{A}}$$治疗,其每一个疗程的成功率均为$${{7}{0}{%}{,}}$$且每一个疗程的成功与否相互独立;其余为第二类,药物$${{A}}$$治疗方式完全无效.在不知道患者所患此疾病的类型,且用药物$${{A}}$$第一个疗程失败的情况下,第二个疗程成功的概率约为()
D
A.$${{0}{.}{4}{5}}$$
B.$${{0}{.}{4}}$$
C.$${{0}{.}{3}{5}}$$
D.$${{0}{.}{2}{9}}$$
2、['二项分布与n重伯努利试验', '用频率估计概率', '相互独立事件的概率']正确率60.0%射击运动中,一次射击最多能得$${{1}{0}}$$环,如图统计了某射击运动员$${{5}{0}}$$次射击命中环数不少于$${{8}}$$环的频数,用频率估计概率,则该运动员在$${{3}}$$次独立射击中,总环数不少于$${{2}{8}}$$环的概率是()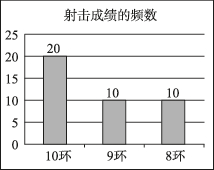
C
A.$$\frac{1 9} {3 2}$$
B.$$\frac{1} {2}$$
C.$$\frac{3 8} {1 2 5}$$
D.$$\frac{3 2} {1 2 5}$$
3、['众数、中位数和平均数', '用频率估计概率']正确率60.0%某市为实现“节能减排,绿色出行”的目标,自$${{2}{0}{1}{8}}$$年起大力推广新能源出租车、网约车.截至目前,全市出租车已有$${{3}{8}{%}}$$换装为新能源汽车,网约车中更是有$${{5}{1}{%}}$$的车辆为新能源汽车.某人从泉城广场通过手机软件打车功能,同时呼叫出租车与网约车,该软件平台向附近$${{4}{2}}$$辆出租车和$${{2}{1}}$$辆网约车推送接单信息(假设平台呼叫范围内新能源车比例与全市区域相同,每位司机接单机会相同),那么该乘客被新能源汽车司机接单的概率约为()
A
A.$$4 2. 3 \%$$
B.
C.$$4 6. 7 \%$$
D.$${{5}{0}{%}}$$
4、['用频率估计概率', '概率的基本性质']正确率80.0%下列关于概率的说法正确的是()
C
A.频率就是概率
B.任何事件的概率都在$${{(}{0}}$$,$${{1}{)}}$$内
C.概率是客观存在的,与试验次数无关
D.概率是随机的,与试验次数有关
5、['用频率估计概率', '分层随机抽样的概念']正确率80.0%某公司有员工$${{3}{0}{0}{0}}$$人,其中研发人员有$${{3}{5}{0}}$$人,销售人员有$${{1}{5}{0}}$$人,其余员工都是工人$${{.}}$$为了调查员工对公司工作环境的满意度,用分层抽样的方法从所有员工中抽取$${{6}{0}}$$人,则工人甲被抽到的概率为()
C
A.$$\frac{1} {6 0}$$
B.$$\frac{1} {2 5 0}$$
C.$$\frac{1} {5 0}$$
D.$$\frac{1} {2 5 0 0}$$
6、['用频率估计概率', '频率分布表与频率分布直方图']正确率60.0%港珠澳大桥位于中国广东省珠江口伶仃洋海域内,是中国境内一项连接香港、珠海和澳门的桥隧工程,因其超大的建筑规模、空前的施工难度和顶尖的建造技术而闻名世界$$\mathrm{. 2 0 1 8}$$年$${{1}{0}}$$月$${{2}{4}}$$日上午$${{9}}$$时开通运营后香港到澳门之间$${{4}}$$个小时的陆路车程极大缩短.为了解实际通行所需时间,随机抽取了$${{n}}$$台车辆进行统计,结果显示这些车辆的通行时间(单位:分钟)都在$$[ 3 5, ~ 5 0 ]$$内,按通行时间分为$$[ 3 5, ~ 3 8 ),$$$$[ 3 8, ~ 4 1 ),$$$$[ 4 1, ~ 4 4 ), ~ [ 4 4, ~ 4 7 ),$$$$[ {\bf4 7}, ~ 5 0 ]$$五组,其中通行时间在$$[ 3 8, ~ 4 7 )$$内的车辆有$${{1}{8}{2}}$$台,频率分布直方图如图所示,则$${{n}{=}}$$()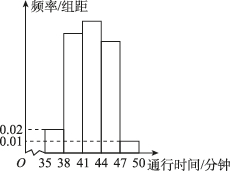
D
A.$${{2}{8}{0}}$$
B.$${{2}{6}{0}}$$
C.$${{2}{5}{0}}$$
D.$${{2}{0}{0}}$$
7、['用频率估计概率']正确率80.0%从某批零件中抽取$${{5}{0}}$$个,然后再从这$${{5}{0}}$$个中抽出$${{4}{0}}$$个进行合格检查,发现合格品有$${{3}{6}}$$个,则该批产品的合格率约为()
C
A.$${{3}{6}{%}}$$
B.$${{7}{2}{%}}$$
C.$${{9}{0}{%}}$$
D.$${{2}{5}{%}}$$
8、['用频率估计概率', '频数与频率']正确率60.0%某校高三$${{(}{1}{)}}$$班$${{5}{0}}$$名学生参加$${{1}{{5}{0}{0}}{m}}$$体能测试,其中$${{2}{3}}$$人的成绩为$${{A}{,}}$$其余人的成绩都是$${{B}}$$或$${{C}}$$.从这$${{5}{0}}$$名学生中任抽$${{1}}$$人,若抽得的人的成绩是$${{B}}$$的概率是$${{0}{.}{4}{,}}$$则抽得的人的成绩是$${{C}}$$的概率是()
A
A.$${{0}{.}{1}{4}}$$
B.$${{0}{.}{2}{0}}$$
C.$${{0}{.}{4}{0}}$$
D.$${{0}{.}{6}{0}}$$
9、['随机模拟', '用频率估计概率']正确率60.0%已知某运动员每次投篮命中的概率都是$${{4}{0}{%}}$$.现采用随机模拟的方法估计该运动员三次投篮恰有一次命中的概率:先由计算器产生$${{0}}$$到$${{9}}$$之间取整数值的随机数,指定$${{1}}$$,$${{2}}$$,$${{3}}$$,$${{4}}$$表示命中,$${{5}}$$,$${{6}}$$,$${{7}}$$,$${{8}}$$,$${{9}}$$,$${{0}}$$表示不命中;再以每三个随机数作为一组,代表三次投篮的结果.经随机模拟产生了如下$${{2}{0}}$$组随机数:$${{9}{0}{7}}$$,$${{9}{6}{6}}$$,$${{1}{9}{1}}$$,$${{9}{2}{5}}$$,$${{2}{7}{1}}$$,$${{9}{3}{2}}$$,$${{8}{1}{2}}$$,$${{4}{5}{8}}$$,$${{5}{6}{9}}$$,$${{6}{8}{3}}$$,$${{4}{3}{1}}$$,$${{2}{5}{7}}$$,$${{3}{9}{3}}$$,$${{0}{2}{7}}$$,$${{5}{5}{6}}$$,$${{4}{8}{8}}$$,$${{7}{3}{0}}$$,$${{1}{1}{3}}$$,$${{5}{3}{7}}$$,$${{9}{8}{9}}$$.据此估计,该运动员三次投篮恰有一次命中的概率为()
D
A.$${{0}{.}{2}{5}}$$
B.$${{0}{.}{2}}$$
C.$${{0}{.}{3}{5}}$$
D.$${{0}{.}{4}}$$
10、['用频率估计概率', '概率的基本性质', '随机事件发生的概率']正确率60.0%某省高考数学试题中,共有$${{1}{2}}$$道选择题,每道选择题有$${{4}}$$个选项,其中只有$${{1}}$$个选项是正确的,即随机选择其中$${{1}}$$个选项正确的概率是$$\frac{1} {4}$$,某人说:“要是都不会做,每题都随机选择其中$${{1}}$$个选项,则一定有$${{3}}$$道题答对.”这个说法()
B
A.正确
B.错误
C.不一定
D.无法解释
1. 解析:首先计算第一类疾病的概率为$$70\%$$,第二类为$$30\%$$。第一个疗程失败的概率为$$P(\text{失败})=0.7 \times 0.3 + 0.3 \times 1 = 0.51$$。在第一个疗程失败的条件下,患者属于第一类的概率为$$P(\text{第一类}|\text{失败})=\frac{0.7 \times 0.3}{0.51}=\frac{7}{17}$$,属于第二类的概率为$$P(\text{第二类}|\text{失败})=\frac{0.3 \times 1}{0.51}=\frac{10}{17}$$。第二个疗程成功的概率为$$\frac{7}{17} \times 0.7 \approx 0.288$$,最接近选项D $$0.29$$。
3. 解析:出租车中新能源车数量为$$42 \times 0.38=15.96$$,网约车中新能源车数量为$$21 \times 0.51=10.71$$。总新能源车数为$$15.96+10.71=26.67$$,总车辆数为$$42+21=63$$。被新能源汽车接单的概率为$$\frac{26.67}{63} \approx 0.423$$,即选项A $$42.3\%$$。
5. 解析:工人数量为$$3000-350-150=2500$$。分层抽样中每个个体被抽到的概率相同,为$$\frac{60}{3000}=\frac{1}{50}$$,故选C。
7. 解析:从$$50$$个中抽取$$40$$个,合格率为$$\frac{36}{40}=0.9$$,因此整批产品的合格率约为$$90\%$$,故选C。
9. 解析:在$$20$$组随机数中,恰有一次命中的组数为$$191, 271, 812, 431, 257, 393, 027, 113, 537$$共$$7$$组(注意$$191$$有两次命中,不计)。实际应为$$5$$组($$271, 431, 257, 027, 113$$),概率为$$\frac{5}{20}=0.25$$,故选A。
.jpg)