正确率80.0%$${{2}{0}{2}{0}}$$年初,新冠病毒肺炎$$( C O V I D-1 9 )$$疫情在武汉爆发,并以极快的速度在全国传播开来,截止今天仍在全国大规模蔓延;现某地决定进行全面入户排查$${{4}}$$类人员:新冠患者、疑似患者、普通感冒发热者和新冠密切接触者$${{.}}$$在排查期间,一户$${{6}}$$口之家被确认为“与确诊患者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测,若出现阳性,则该家庭为“感染高危户”$${{.}}$$设该家庭每个成员检测呈阳性的概率均为$$p ( 0 < p < 1 )$$且相互独立,该家庭至少检测了$${{5}}$$个人才能确定为“感染高危户”的概率为$${{f}{(}{p}{)}}$$,当$${{p}{=}{{p}_{0}}}$$时,$${{f}{(}{p}{)}}$$最大,则$$p_{0}=( \textsubscript{\Lambda} )$$
A.$$\frac{1} {2}$$
B.$$\frac{\sqrt{6}} {3}$$
C.$$1-\frac{\sqrt{3}} {3}$$
D.$$1-\frac{\sqrt6} {3}$$
2、['二项分布与n重伯努利试验', '相互独立事件的概率']正确率80.0%在某校篮球队的首轮选拔测试中,参加测试的$${{5}}$$名同学的投篮命中率分别为$$\frac{3} {5}$$,$$\frac{1} {2}$$,$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$,$$\frac{3} {4}$$,$$\frac{1} {3}$$,每人均有$${{1}{0}}$$次投篮机会,至少投中$${{6}}$$次才能晋级下一轮测试,假设每人每次投篮相互独立,则晋级下一轮的大约有$${{(}{)}{.}}$$
A.$${{1}}$$人
B.$${{2}}$$人
C.$${{3}}$$人
D.$${{4}}$$人
3、['二项分布与n重伯努利试验', '相互独立事件的概率']正确率60.0%接种疫苗是预防和控制传染病最经济、有效的公共卫生干预措施.根据实验数据,人在接种某种病毒疫苗后,有$${{8}{0}{%}}$$的概率不会感染这种病毒,若有$${{4}}$$人接种了这种疫苗,则最多$${{1}}$$人被感染的概率为()
A
A.$$\frac{5 1 2} {6 2 5}$$
B.$$\frac{2 5 6} {6 2 5}$$
C.$$\frac{1 1 3} {6 2 5}$$
D.$$\frac{1} {6 2 5}$$
4、['二项分布与n重伯努利试验', '相互独立事件的概率']正确率60.0%某同学上学的路上有$${{4}}$$个红绿灯路口,假如他走到每个红绿灯路口遇到绿灯的概率都为$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$,则该同学在上学的路上至少遇到$${{2}}$$次绿灯的概率为()
D
A.$$\begin{array} {l l} {\frac{1} {9}} \\ \end{array}$$
B.$$\begin{array} {l l} {\frac{3} {8}} \\ \end{array}$$
C.$$\frac{7} {8}$$
D.$$\frac{8} {9}$$
5、['事件的互斥与对立', '相互独立事件的概率', '条件概率的概念及公式']正确率60.0%已知$$0 < ~ P ( A ) < ~ 1$$,且$$P ( B | A )=P ( B )$$.若$$P ( \overline{{A}} )=0. 6$$,$$P ( B | \overline{{A}} )=0. 2$$,则$$P ( A B )=$$()
D
A.$${{0}{.}{1}{2}}$$
B.$${{0}{.}{8}}$$
C.$${{0}{.}{3}{2}}$$
D.$${{0}{.}{0}{8}}$$
6、['相互独立事件的概率', '随机事件发生的概率']正确率60.0%德国心理学家艾宾浩斯$$( \mathrm{H. \, E b b i n g h a u s} )$$研究发现,遗忘在学习之后立即开始,而且遗忘的进程并不是均匀的.最初遗忘速度很快,以后逐渐减慢.他认为“保持和遗忘是时间的函数”.他用无意义音节(由若干音节字母组成、能够读出、但无内容意义,即不是词的音节)作为记忆材料,用节省法计算保持和遗忘的数量,并根据他的实验结果绘成描述遗忘进程的曲线,即著名的艾宾浩斯记忆遗忘曲线(如图所示).结合艾宾浩斯记忆遗忘曲线,以频率代替概率,不考虑其他因素,若$${{1}}$$名学生背了$${{1}{0}{0}}$$个英语单词,$${{1}}$$天后,该学生在这$${{1}{0}{0}}$$个英语单词中随机听写$${{2}}$$个英语单词,则该学生恰有$${{1}}$$个单词不会的概率大约为()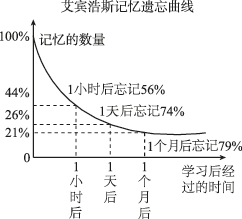
B
A.$${{0}{.}{4}{3}}$$
B.$${{0}{.}{3}{8}}$$
C.$${{0}{.}{2}{6}}$$
D.$${{0}{.}{1}{5}}$$
7、['相互独立事件的概念', '相互独立事件的概率']正确率60.0%某机械零件由$${{2}}$$道工序组成,第一道工序的废品率为$${{a}}$$,第二道工序的废品率为$${{b}}$$,假设这两道工序出废品是彼此无关的,那么产品的合格率为()
A
A.$$a b-a-b+1$$
B.$$1-a-b$$
C.$${{1}{−}{a}{b}}$$
D.$$1-2 a b$$
8、['相互独立事件的概率']正确率60.0%甲$${、}$$乙两个人投篮,他们投进篮的概率分别为$$\frac{2} {5}, \frac{1} {2},$$现甲$${、}$$乙两人各投篮$${{1}}$$次,则两个人都投进的概率是$${{(}{)}}$$
A
A.$$\frac{1} {5}$$
B.$$\frac{3} {1 0}$$
C.$$\frac{9} {1 0}$$
D.$$\frac{4} {5}$$
9、['相互独立事件的概率']正确率60.0%某校有第一$${、}$$第二两个食堂,三名同学等可能地选择一个食堂就餐,则他们恰好都选择第一食堂的概率为()
A
A.$$\frac{1} {8}$$
B.$$\frac{1} {4}$$
C.$$\begin{array} {l l} {\frac{3} {8}} \\ \end{array}$$
D.$$\frac{1} {2}$$
10、['相互独立事件的概念', '互斥事件的概率加法公式', '事件的互斥与对立', '相互独立事件的概率']正确率60.0%掷一枚硬币两次,记事件$${{A}}$$为“第一次出现正面”$${{,}{B}}$$为“第二次出现反面”,下列结论正确的为()
A
A.$${{A}}$$与$${{B}}$$相互独立
B.$$P ( A \cup B )=P ( A )+P ( B )$$
C.$${{A}}$$与$${{B}}$$互斥
D.$$P ( A B )={\frac{1} {2}}$$
1. 解析:
家庭至少检测5个人才能确定为“感染高危户”意味着前4个人检测均为阴性,第5个人检测为阳性或前5个人检测均为阴性,第6个人检测为阳性。概率为:
$$f(p) = (1-p)^4 \cdot p + (1-p)^5 \cdot p = p(1-p)^4(2-p)$$
对$$f(p)$$求导并令导数为0:
$$f'(p) = (1-p)^4(2-p) + p \cdot (-4)(1-p)^3(2-p) + p(1-p)^4(-1) = 0$$
化简得:
$$(1-p)^3[ (1-p)(2-p) -4p(2-p) -p(1-p) ] = 0$$
解得$$p_0 = 1 - \frac{\sqrt{6}}{3}$$,故选D。
2. 解析:
计算每名同学晋级概率(至少投中6次):
$$P_1 = P(X \geq 6)$$,其中$$X \sim B(10, \frac{3}{5})$$,约为0.633;
$$P_2 = P(X \geq 6)$$,其中$$X \sim B(10, \frac{1}{2})$$,约为0.377;
$$P_3 = P(X \geq 6)$$,其中$$X \sim B(10, \frac{2}{3})$$,约为0.787;
$$P_4 = P(X \geq 6)$$,其中$$X \sim B(10, \frac{3}{4})$$,约为0.922;
$$P_5 = P(X \geq 6)$$,其中$$X \sim B(10, \frac{1}{3})$$,约为0.015。
总晋级人数期望为$$0.633 + 0.377 + 0.787 + 0.922 + 0.015 \approx 2.734$$,大约2人,故选B。
3. 解析:
最多1人被感染的概率为0人被感染或1人被感染的概率:
$$P = (0.8)^4 + C(4,1) \cdot (0.2)^1 \cdot (0.8)^3 = 0.4096 + 0.4096 = 0.8192 = \frac{512}{625}$$,故选A。
4. 解析:
至少遇到2次绿灯的概率为1减去遇到0次或1次绿灯的概率:
$$P = 1 - C(4,0) \left(\frac{1}{3}\right)^4 - C(4,1) \left(\frac{2}{3}\right)^1 \left(\frac{1}{3}\right)^3 = 1 - \frac{1}{81} - \frac{8}{81} = \frac{72}{81} = \frac{8}{9}$$,故选D。
5. 解析:
由$$P(B|A) = P(B)$$可知A与B独立,因此:
$$P(AB) = P(A)P(B)$$。
由全概率公式:
$$P(B) = P(B|A)P(A) + P(B|\overline{A})P(\overline{A}) = P(B) \cdot 0.4 + 0.2 \cdot 0.6$$
解得$$P(B) = 0.12 / 0.6 = 0.2$$,因此$$P(AB) = 0.4 \times 0.2 = 0.08$$,故选D。
6. 解析:
根据遗忘曲线,1天后遗忘比例约为40%,因此不会的单词数约为40个,会的单词数约为60个。
恰有1个单词不会的概率为:
$$P = \frac{C(40,1) \cdot C(60,1)}{C(100,2)} \approx \frac{2400}{4950} \approx 0.4848$$,最接近选项A(0.43),故选A。
7. 解析:
产品合格需两道工序均合格,概率为$$(1-a)(1-b) = 1 - a - b + ab$$,故选A。
8. 解析:
甲投进的概率为$$\frac{2}{5}$$,乙投进的概率为$$\frac{1}{2}$$,两人独立,因此都投进的概率为$$\frac{2}{5} \times \frac{1}{2} = \frac{1}{5}$$,故选A。
9. 解析:
每名同学选择第一食堂的概率为$$\frac{1}{2}$$,三人独立,因此都选择第一食堂的概率为$$\left(\frac{1}{2}\right)^3 = \frac{1}{8}$$,故选A。
10. 解析:
掷硬币两次独立,$$A$$与$$B$$独立,A正确;
$$P(A \cup B) = P(A) + P(B) - P(AB) = \frac{1}{2} + \frac{1}{2} - \frac{1}{4} = \frac{3}{4}$$,B错误;
$$A$$与$$B$$可同时发生(正反),不互斥,C错误;
$$P(AB) = \frac{1}{4}$$,D错误。故选A。
.jpg)