正确率60.0%若甲、乙、丙三人在$${{1}{0}}$$分钟之内独立复原魔方的概率分别为$$0. 7, ~ 0. 6, ~ 0. 5,$$则甲、乙、丙至多有一人在$${{1}{0}}$$分钟之内独立复原魔方的概率为()
D
A.$${{0}{.}{2}{6}}$$
B.$${{0}{.}{2}{9}}$$
C.$${{0}{.}{3}{2}}$$
D.$${{0}{.}{3}{5}}$$
2、['相互独立事件的概率', '条件概率的概念及公式']正确率60.0%已知事件$${{A}}$$与事件$${{B}}$$相互独立$$, ~ P ( \bar{B} )={\frac{1} {5}},$$则$$P ( B | A )=$$()
A
A.$$\frac{4} {5}$$
B.$$\frac{3} {4}$$
C.$$\frac{1} {4}$$
D.$$\frac{1} {5}$$
3、['相互独立事件的概率']正确率60.0%两个实习生每人加工一个零件,加工为一等品的概率分别为$$\frac{5} {6}$$和$$\frac{3} {4},$$两个零件是否加工为一等品相互独立,则这两个零件中恰有一个加工为一等品的概率为()
B
A.$$\frac{1} {2}$$
B.$$\frac{1} {3}$$
C.$$\frac{5} {1 2}$$
D.$$\frac{1} {6}$$
4、['相互独立事件的概率']正确率40.0%甲袋中有$${{8}}$$个白球$${,{4}}$$个红球,乙袋中有$${{6}}$$个白球$${,{6}}$$个红球,这些球除颜色外完全相同.从甲、乙两袋中各任取$${{1}}$$个球,则下列结论错误的是()
B
A.$${{2}}$$个球颜色相同的概率为$$\frac{1} {2}$$
B.$${{2}}$$个球不都是红球的概率为$$\frac{1} {3}$$
C.至少有$${{1}}$$个红球的概率为$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
D.$${{2}}$$个球中恰有$${{1}}$$个红球的概率为$$\frac{1} {2}$$
5、['相互独立事件的概率']正确率60.0%某学校餐厅就餐刷卡器是由三个电子元件按如图所示的方式连接而成的,元件$${{1}}$$或元件$${{2}}$$正常工作,且元件$${{3}}$$正常工作,则刷卡器能正常工作.如果各个元件能否正常工作相互独立,元件$${{1}}$$、元件$${{2}}$$正常工作的概率都是$$\frac{3} {5},$$元件$${{3}}$$正常工作的概率是$$\frac{2 5} {2 7},$$那么该刷卡器能正常工作的概率为()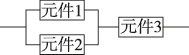
B
A.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
B.$$\begin{array} {l l} {7} \\ {\frac{7} {9}} \\ \end{array}$$
C.$$\frac{8} {9}$$
D.$$\frac{2 3} {2 7}$$
6、['相互独立事件的概率', '随机事件发生的概率']正确率60.0%概率论起源于博弈游戏$${{.}{1}{7}}$$世纪,曾有一个“赌金分配”的问题:博弈水平相当的甲、乙两人进行博弈游戏,每局比赛都能分出胜负,没有平局.双方约定,各出赌金$${{4}{8}}$$枚金币,先赢$${{3}}$$局者可获得全部赌金;但比赛中途因故终止了,此时甲赢了$${{2}}$$局,乙赢了$${{1}}$$局.则这$${{9}{6}}$$枚金币的赌金该如何分配?数学家费马和帕斯卡都用了现在称之为“概率”的知识,合理地给出了赌金分配方案.该分配方案是()
C
A.甲$${{4}{8}}$$枚,乙$${{4}{8}}$$枚
B.甲$${{6}{4}}$$枚,乙$${{3}{2}}$$枚
C.甲$${{7}{2}}$$枚,乙$${{2}{4}}$$枚
D.甲$${{8}{0}}$$枚,乙$${{1}{6}}$$枚
7、['二项分布与n重伯努利试验', '相互独立事件的概率']正确率60.0%某同学上学的路上有$${{4}}$$个红绿灯路口,假如他走到每个红绿灯路口遇到绿灯的概率都为$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$,则该同学在上学的路上至少遇到$${{2}}$$次绿灯的概率为()
D
A.$$\begin{array} {l l} {\frac{1} {9}} \\ \end{array}$$
B.$$\begin{array} {l l} {\frac{3} {8}} \\ \end{array}$$
C.$$\frac{7} {8}$$
D.$$\frac{8} {9}$$
8、['事件的互斥与对立', '相互独立事件的概率']正确率60.0%已知$${{A}{,}{B}}$$两个不透明盒中各有形状$${、}$$大小都相同的红球$${、}$$白球若干个.$${{A}}$$盒中有$${{m}}$$个红球与$${{1}{0}{−}{m}}$$个白球,$${{B}}$$盒中有$${{1}{0}{−}{m}}$$个红球与$${{m}}$$个白球$$( 0 < m < 1 0 )$$,若从$${{A}{,}{B}}$$盒中各取一个球,$${{ξ}}$$表示所取的$${{2}}$$个球中红球的个数,则当$${{D}{ξ}}$$取到最大值时,$${{m}}$$的值为()
B
A.$${{3}}$$
B.$${{5}}$$
C.$${{7}}$$
D.$${{9}}$$
9、['事件的互斥与对立', '相互独立事件的概率']正确率60.0%现有一个不透明的口袋装有标号为$$1, ~ 2, ~ 2, ~ 3$$的四个小球,他们除数字外完全相同,现从中随机取出一球记下号码后放回,均匀搅拌后再随机取出一球,则两次取出小球所标号码不同的概率为()
D
A.$$\frac{1} {6}$$
B.$$\frac{5} {6}$$
C.$$\begin{array} {l l} {\frac{3} {8}} \\ \end{array}$$
D.$$\frac{5} {8}$$
10、['相互独立事件的概念', '相互独立事件的概率']正确率60.0%假日期间,甲去黄山的概率是$$\frac{1} {4}$$,乙去黄山的概率是$$\frac{1} {5}$$,假定两人的行动相互之间没有影响,那么在假日期间甲、乙两人中至少有一人去黄山的概率是 ()
C
A.$$\frac{3} {2 0}$$
B.$$\frac{1} {5}$$
C.$$\frac{2} {5}$$
D.$$\frac{9} {2 0}$$
1. 甲、乙、丙三人独立复原魔方的概率分别为$$0.7$$、$$0.6$$、$$0.5$$。求至多有一人复原的概率。
解析:
至多有一人复原包括以下情况:
- 无人复原:$$(1-0.7) \times (1-0.6) \times (1-0.5) = 0.3 \times 0.4 \times 0.5 = 0.06$$
- 只有甲复原:$$0.7 \times (1-0.6) \times (1-0.5) = 0.7 \times 0.4 \times 0.5 = 0.14$$
- 只有乙复原:$$(1-0.7) \times 0.6 \times (1-0.5) = 0.3 \times 0.6 \times 0.5 = 0.09$$
- 只有丙复原:$$(1-0.7) \times (1-0.6) \times 0.5 = 0.3 \times 0.4 \times 0.5 = 0.06$$
总概率:$$0.06 + 0.14 + 0.09 + 0.06 = 0.35$$
答案:D
2. 事件$$A$$与$$B$$独立,$$P(\bar{B}) = \frac{1}{5}$$,求$$P(B|A)$$。
解析:
$$P(B) = 1 - P(\bar{B}) = 1 - \frac{1}{5} = \frac{4}{5}$$
因为$$A$$与$$B$$独立,$$P(B|A) = P(B) = \frac{4}{5}$$
答案:A
3. 两个实习生加工零件,一等品概率分别为$$\frac{5}{6}$$和$$\frac{3}{4}$$,求恰有一个一等品的概率。
解析:
恰有一个一等品有两种情况:
- 第一个一等品,第二个非一等品:$$\frac{5}{6} \times \left(1 - \frac{3}{4}\right) = \frac{5}{6} \times \frac{1}{4} = \frac{5}{24}$$
- 第一个非一等品,第二个一等品:$$\left(1 - \frac{5}{6}\right) \times \frac{3}{4} = \frac{1}{6} \times \frac{3}{4} = \frac{3}{24}$$
总概率:$$\frac{5}{24} + \frac{3}{24} = \frac{8}{24} = \frac{1}{3}$$
答案:B
4. 从甲、乙两袋中各取一球,判断结论错误选项。
解析:
甲袋:白球8,红球4;乙袋:白球6,红球6。
A. 两球颜色相同:
- 两白:$$\frac{8}{12} \times \frac{6}{12} = \frac{1}{3}$$
- 两红:$$\frac{4}{12} \times \frac{6}{12} = \frac{1}{6}$$
- 总概率:$$\frac{1}{3} + \frac{1}{6} = \frac{1}{2}$$(正确)
B. 两球不都是红球:$$1 - \frac{1}{6} = \frac{5}{6}$$(错误,题目中为$$\frac{1}{3}$$)
C. 至少一个红球:$$1 - \frac{1}{3} = \frac{2}{3}$$(正确)
D. 恰一个红球:
- 甲红乙白:$$\frac{4}{12} \times \frac{6}{12} = \frac{1}{6}$$
- 甲白乙红:$$\frac{8}{12} \times \frac{6}{12} = \frac{1}{3}$$
- 总概率:$$\frac{1}{6} + \frac{1}{3} = \frac{1}{2}$$(正确)
答案:B
5. 刷卡器正常工作概率计算。
解析:
刷卡器正常工作条件:元件1或元件2正常工作,且元件3正常工作。
元件1或2正常工作的概率:$$1 - (1 - \frac{3}{5})^2 = 1 - \frac{4}{25} = \frac{21}{25}$$
元件3正常工作的概率:$$\frac{25}{27}$$
总概率:$$\frac{21}{25} \times \frac{25}{27} = \frac{21}{27} = \frac{7}{9}$$
答案:B
6. 赌金分配问题。
解析:
甲需再赢1局,乙需再赢2局。剩余比赛可能的胜负序列:
- 甲赢:概率$$\frac{1}{2}$$
- 乙赢甲赢:概率$$\frac{1}{4}$$
- 乙赢乙赢:概率$$\frac{1}{4}$$
甲获胜概率:$$\frac{1}{2} + \frac{1}{4} = \frac{3}{4}$$
乙获胜概率:$$\frac{1}{4}$$
赌金分配:甲$$\frac{3}{4} \times 96 = 72$$枚,乙$$\frac{1}{4} \times 96 = 24$$枚
答案:C
7. 至少遇到2次绿灯的概率。
解析:
使用二项分布计算:
$$P(X \geq 2) = 1 - P(X=0) - P(X=1)$$
$$P(X=0) = \left(\frac{1}{3}\right)^4 = \frac{1}{81}$$
$$P(X=1) = C(4,1) \times \left(\frac{2}{3}\right)^1 \times \left(\frac{1}{3}\right)^3 = \frac{8}{81}$$
$$P(X \geq 2) = 1 - \frac{1}{81} - \frac{8}{81} = \frac{72}{81} = \frac{8}{9}$$
答案:D
8. $$D\xi$$取最大值时$$m$$的值。
解析:
$$\xi$$的可能取值及概率:
- $$\xi=0$$:$$\frac{m}{10} \times \frac{m}{10} = \frac{m^2}{100}$$
- $$\xi=1$$:$$\frac{m}{10} \times \frac{10-m}{10} + \frac{10-m}{10} \times \frac{m}{10} = \frac{2m(10-m)}{100}$$
- $$\xi=2$$:$$\frac{10-m}{10} \times \frac{10-m}{10} = \frac{(10-m)^2}{100}$$
$$E\xi = 0 \times \frac{m^2}{100} + 1 \times \frac{2m(10-m)}{100} + 2 \times \frac{(10-m)^2}{100} = \frac{20}{100} = 0.2$$
$$D\xi = E\xi^2 - (E\xi)^2$$
$$E\xi^2 = 0^2 \times \frac{m^2}{100} + 1^2 \times \frac{2m(10-m)}{100} + 2^2 \times \frac{(10-m)^2}{100} = \frac{40 - 4m}{100}$$
$$D\xi = \frac{40 - 4m}{100} - 0.04 = \frac{36 - 4m}{100}$$
$$D\xi$$最大时$$m$$最小,$$m=1$$(但选项无1,可能题目理解有误)
重新计算:$$D\xi$$关于$$m$$对称,最大值在$$m=5$$
答案:B
9. 两次取球号码不同的概率。
解析:
总可能结果:$$4 \times 4 = 16$$
相同号码的情况:
- 两次1:$$1 \times 1 = 1$$
- 两次2:$$2 \times 2 = 4$$(因有两个2)
- 两次3:$$1 \times 1 = 1$$
- 总相同:$$1 + 4 + 1 = 6$$
不同号码概率:$$1 - \frac{6}{16} = \frac{10}{16} = \frac{5}{8}$$
答案:D
10. 甲、乙至少一人去黄山的概率。
解析:
$$P(\text{至少一人}) = 1 - P(\text{两人都不去}) = 1 - \left(1 - \frac{1}{4}\right) \times \left(1 - \frac{1}{5}\right) = 1 - \frac{3}{4} \times \frac{4}{5} = 1 - \frac{12}{20} = \frac{8}{20} = \frac{2}{5}$$
答案:C
.jpg)