正确率80.0%试验$${{E}}$$:有红、黄、蓝三种颜色的旗帜各$${{3}}$$面,在每种颜色的$${{3}}$$面旗帜上分别标上号码$${\bf1}, ~ {\bf2}, ~ {\bf3},$$现从红、黄、蓝三种颜色的旗帜中各取$${{1}}$$面.记事件$${{A}}$$为“$${{3}}$$面旗帜的号码均不相同”,则此事件所包含的样本点个数为()
A
A.$${{6}}$$
B.$${{8}}$$
C.$${{9}}$$
D.$${{1}{0}}$$
2、['有限样本空间']正确率80.0%已知$${{a}{∈}}$${$$0, ~ 1, ~ 2$$}$${,{b}{∈}}$${$$1, ~ 2, ~ 3$$},则由一次函数$$y=a x+b$$构成的样本空间中的样本点的个数为()
B
A.$${{5}}$$
B.$${{6}}$$
C.$${{8}}$$
D.$${{9}}$$
3、['有限样本空间']正确率80.0%将一枚质地均匀且四个面上分别标有$$1, ~ 2, ~ 3, ~ 4$$的正四面体先后抛掷两次,其底面落于桌面上,记第一次底面的数字为$${{x}{,}}$$第二次底面的数字为$${{y}}$$.用$$( x, ~ y )$$表示一个样本点.若事件$${{A}}$$表示$$\frac{x} {y}$$为整数,则事件$${{A}}$$包含的样本点的个数为()
B
A.$${{7}}$$
B.$${{8}}$$
C.$${{9}}$$
D.$${{1}{0}}$$
4、['有限样本空间']正确率80.0%要从甲、乙、丙、丁四位同学中选$${{2}}$$人参加一项活动,则该试验的样本空间中包含的样本点个数为()
C
A.$${{2}}$$
B.$${{4}}$$
C.$${{6}}$$
D.$${{8}}$$
5、['古典概型的应用', '有限样本空间']正确率80.0%现将三张分别印有“$${{A}}$$”“$${{B}}$$”“$${{C}}$$”的卡片(卡片的形状、大小和质地完全相同)放入不透明的盒子中.若从盒子中依次有放回地取出两张卡片,则一张为“$${{A}}$$”,一张为“$${{B}}$$”的概率是()
C
A.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
B.$$\frac{1} {3}$$
C.$$\begin{array} {l l} {\frac{2} {9}} \\ \end{array}$$
D.$$\begin{array} {l l} {\frac{1} {9}} \\ \end{array}$$
6、['有限样本空间']正确率80.0%在$$1, ~ 2, ~ 3, ~ 4$$四个数中随机地抽取一个数记为$${{a}{,}}$$再在剩余的三个数中随机地抽取一个数记为$${{b}{,}}$$则“$$\frac{a} {b}$$不是整数”的概率为()
C
A.$$\frac{1} {3}$$
B.$$\frac{1} {4}$$
C.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
D.$$\frac{3} {4}$$
7、['有限样本空间']正确率80.0%抛掷两枚骰子,记第一枚骰子掷出的点数与第二枚骰子掷出的点数之差为$${{ξ}{,}}$$则{$${{ξ}{>}{4}}$$}表示的试验结果是()
A
A.第一枚$${{6}}$$点,第二枚$${{1}}$$点
B.第一枚$${{5}}$$点,第二枚$${{1}}$$点
C.第一枚$${{2}}$$点,第二枚$${{6}}$$点
D.第一枚$${{6}}$$点,第二枚$${{2}}$$点
8、['有限样本空间', '随机事件']正确率60.0%袋中有$${{2}}$$个红色的变形金刚$${,{2}}$$个白色的变形金刚$${,{2}}$$个黑色的变形金刚,从里面任意取$${{2}}$$个变形金刚,下列事件中不是基本事件的为()
D
A.恰好有$${{2}}$$个红色的变形金刚
B.恰好有$${{2}}$$个黑色的变形金刚
C.恰好有$${{2}}$$个白色的变形金刚
D.至少有$${{1}}$$个红色的变形金刚
9、['古典概型的概率计算公式', '古典概型的应用', '有限样本空间']正确率60.0%同时投掷两个骰子,则向上的点数之差的绝对值为$${{4}}$$的概率是$${{(}{)}}$$
C
A.
B.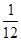
C.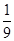
D.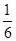
正确率80.0%关于样本点$${、}$$样本空间,下列说法错误的是()
D
A.样本点是构成样本空间的元素
B.样本点是构成随机事件的元素
C.随机事件是样本空间的子集
D.随机事件中样本点的个数可能比样本空间中的多
1. 解析:
从红、黄、蓝三种颜色的旗帜中各取1面,每面旗帜的号码为1、2、3。要求3面旗帜的号码均不相同,即红、黄、蓝旗帜的号码互不重复。
号码的组合方式为全排列:$$3! = 6$$ 种。
因此,事件A包含的样本点个数为 $$6$$,选 A。
2. 解析:
$$a$$ 有3种取值(0、1、2),$$b$$ 有3种取值(1、2、3)。
样本空间中的样本点个数为 $$3 \times 3 = 9$$,选 D。
3. 解析:
抛掷两次正四面体,样本空间为 $$(x, y)$$,其中 $$x, y \in \{1, 2, 3, 4\}$$。
要求 $$\frac{x}{y}$$ 为整数,即 $$x$$ 是 $$y$$ 的倍数。符合条件的样本点有:
$$(1,1), (2,1), (2,2), (3,1), (3,3), (4,1), (4,2), (4,4)$$,共 $$8$$ 个。
因此,选 B。
4. 解析:
从4位同学中选2人,组合数为 $$C(4,2) = 6$$。
样本空间中包含的样本点个数为 $$6$$,选 C。
5. 解析:
每次取卡片有3种可能(A、B、C),有放回地取两次,样本空间大小为 $$3 \times 3 = 9$$。
一张为A,一张为B的情况有两种顺序:$$(A, B)$$ 和 $$(B, A)$$。
概率为 $$\frac{2}{9}$$,选 C。
6. 解析:
从4个数中取 $$a$$,再从剩下的3个数中取 $$b$$,样本空间大小为 $$4 \times 3 = 12$$。
$$\frac{a}{b}$$ 为整数的情况有:$$(2,1), (3,1), (4,1), (4,2)$$,共4种。
因此,“$$\frac{a}{b}$$ 不是整数”的情况有 $$12 - 4 = 8$$ 种,概率为 $$\frac{8}{12} = \frac{2}{3}$$,选 C。
7. 解析:
设第一枚骰子点数为 $$x$$,第二枚为 $$y$$,要求 $$x - y > 4$$。
选项A:$$6 - 1 = 5 > 4$$,符合条件。
选项B:$$5 - 1 = 4$$ 不满足。
选项C:$$2 - 6 = -4$$ 不满足。
选项D:$$6 - 2 = 4$$ 不满足。
因此,选 A。
8. 解析:
基本事件是单一可能的结果,而“至少有1个红色的变形金刚”包含多种情况(1红1白、1红1黑、2红等),不是基本事件。
因此,选 D。
9. 解析:
两个骰子的点数差的绝对值为4,可能的情况有:
$$(1,5), (5,1), (2,6), (6,2)$$,共4种。
样本空间大小为 $$6 \times 6 = 36$$,概率为 $$\frac{4}{36} = \frac{1}{9}$$。
因此,选 D。
10. 解析:
选项D错误,因为随机事件是样本空间的子集,其样本点的个数不可能比样本空间多。
因此,选 D。
.jpg)