.jpg)
正确率40.0%甲、乙、丙三人玩踢毽子游戏，第一次由甲把毽子踢给其他二人中的一人，第二次由得到毽子的人再踢给其他二人中的一人，这样一共踢了$${{3}}$$次，则第$${{3}}$$次毽子仍回到甲的概率为$${{(}{)}}$$
A.$$\frac{1} {2}$$
B.$$\frac{1} {3}$$
C.$$\frac{1} {4}$$
D.$$\frac{1} {8}$$
2、['古典概型']正确率80.0%一个袋中有$${{6}}$$个大小和质地相同的球，其中红球$${{4}}$$个，黑球$${{2}}$$个，现从中不放回地依次随机摸取$${{2}}$$次，每次摸出$${{1}}$$个球，则第二次摸出的球是红球的概率为$${{(}{)}}$$
A.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
B.$$\begin{array} {l l} {5} \\ {\frac{5} {9}} \\ \end{array}$$
C.$$\begin{array} {l l} {\frac{4} {9}} \\ \end{array}$$
D.$$\frac{1} {3}$$
3、['古典概型']正确率80.0%若$$a^{2}+b^{2}=c^{2}$$，则$${{a}}$$，$${{b}}$$，$${{c}}$$三个数称之为勾股数，从$${{3}}$$，$${{4}}$$，$${{1}{2}}$$，$${{1}{3}}$$中任取两个，能和$${{5}}$$组成勾股数的概率是$${{(}{)}}$$
A.$$\frac{1} {6}$$
B.$$\frac{1} {3}$$
C.$$\frac{1} {4}$$
D.$$\frac{1} {2}$$
4、['古典概型']正确率80.0%在一个不透明的袋中有$${{4}}$$个红球和$${{n}}$$个黑球，现从袋中有放回地随机摸出$${{2}}$$个球，已知取出的球中至少有一个红球的概率为$$\frac{8} {9}$$，则$${{n}{=}{(}{)}}$$
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
5、['条件概率'， '古典概型']正确率80.0%现有$${{5}}$$个节目准备参加比赛，其中$${{3}}$$个舞蹈类节目，$${{2}}$$个语言类节目$${{.}}$$如果不放回地依次抽取$${{2}}$$个节目，则在第$${{1}}$$次抽到舞蹈类节目的条件下，第$${{2}}$$次抽到语言类节目的概率为$${{(}{)}}$$
A.$$\frac{3} {4}$$
B.$$\frac{1} {2}$$
C.$$\frac{1} {4}$$
D.$$\frac{1} {3}$$
6、['古典概型']正确率80.0%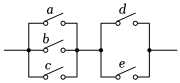
有一组电路开关如图所示，现在开关$${{a}}$$、$${{b}}$$、$${{c}}$$、$${{d}}$$、$${{e}}$$是处于断开状态，任意闭合其中的两个，则电路接通的概率是$${{(}{)}}$$
A.$$\frac{1} {5}$$
B.$$\frac{2} {5}$$
C.$$\frac{3} {5}$$
D.$$\frac{4} {5}$$
7、['古典概型']正确率80.0%在含有$${{3}}$$个白球，$${{2}}$$个黑球$${{(}}$$它们除颜色外，其余均相同$${{)}}$$的箱子里不放回地抽取$${{2}}$$个球，恰好一个为黑球的概率为$${{(}{)}}$$
A.$$\frac{2} {5}$$
B.$$\frac{1} {2}$$
C.$$\frac{3} {5}$$
D.$$\frac{7} {1 0}$$
8、['古典概型']正确率80.0%某足球训练营为提高学员的足球水平、计划对学员们颠球、控球、带球、传球、停球这五项基本功进行加训$${{.}}$$要求学员在周一到周三这三天内完成这五项基本功加训任务，每天最多参训三项基本功加训，且每项基本功只训练一天$${{.}}$$则某学员颠球和传球在同一天完成加训的概率是$${{(}{)}}$$
A.$$\begin{array} {l l} {\frac{2} {7}} \\ \end{array}$$
B.$$\begin{array} {l l} {\frac{3} {7}} \\ \end{array}$$
C.$$\begin{array} {l l} {\frac{4} {7}} \\ \end{array}$$
D.$$\begin{array} {l l} {5} \\ {\frac{5} {7}} \\ \end{array}$$
9、['古典概型']正确率80.0%从$${{2}}$$，$${{3}}$$，$${{4}}$$三个数中任选$${{2}}$$个，分别作为圆柱的高和底面半径，则此圆柱的体积大于$${{2}{0}{π}}$$的概率为$${{(}{)}}$$
A.$$\frac{1} {3}$$
B.$$\frac{1} {2}$$
C.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
D.$$\frac{5} {6}$$
10、['古典概型']正确率80.0%从分别写有$${{1}}$$，$${{2}}$$，$${{3}}$$，$${{4}}$$，$${{5}}$$，$${{6}}$$的$${{6}}$$张卡片中无放回随机抽取$${{2}}$$张，则抽到的$${{2}}$$张卡片上的数字之和是$${{3}}$$的倍数的概率为$${{(}{)}}$$
A.$$\frac{1} {5}$$
B.$$\frac{1} {3}$$
C.$$\frac{2} {5}$$
D.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
1. 甲、乙、丙三人踢毽子游戏的概率问题：
路径1：甲→乙→甲→乙或丙
路径2：甲→丙→甲→乙或丙
只有这两种情况第三次会回到甲，每种情况的概率为 $$ \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = \frac{1}{8} $$，总概率为 $$ \frac{1}{8} + \frac{1}{8} = \frac{1}{4} $$。 正确答案：C.$$\frac{1} {4}$$
2. 第二次摸出红球的概率问题：
A.$$\frac{2} {3}$$
3. 勾股数的概率问题：
A.$$\frac{1} {6}$$
4. 袋中红球和黑球的数量问题：
B.$${{2}}$$
5. 条件概率问题：
B.$$\frac{1} {2}$$
6. 电路开关接通的概率问题：
B.$$\frac{2} {5}$$
7. 不放回抽取恰好一个黑球的概率问题：
C.$$\frac{3} {5}$$
8. 颠球和传球同一天完成的概率问题：
B.$$\frac{3} {7}$$
9. 圆柱体积大于 $$ 20\pi $$ 的概率问题：
B.$$\frac{1} {2}$$
10. 两张卡片数字之和为3的倍数的概率问题：
B.$$\frac{1} {3}$$