正确率60.0%在某线路中有$${{4}}$$个自动控制的常开开关$$A, ~ B, ~ C, ~ D$$连接在一起(如图所示),假定在某段时间内开关$${{A}{,}{D}}$$能够闭合的概率都是$${{0}{.}{7}{,}}$$开关$${{B}{,}{C}}$$能够闭合的概率都是$${{0}{.}{8}{,}}$$则在这段时间内该线路能正常工作的概率为()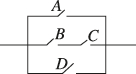
A
A.$$0. 9 6 7 6$$
B.$$0. 9 9 8 2$$
C.$$0. 3 1 3 6$$
D.$$0. 9 6 7 4$$
2、['统计与概率的应用', '随机事件发生的概率']正确率60.0%某卫生部门为了调查某地居民垃圾分类的落实情况,随机抽取该地$${{3}{0}{0}}$$人,并平均分成三组.调查中使用了以下两个问题:
问题一:你是否是第一组的居民?
问题二:你是否经常乱丢垃圾?
调查者设计了一个随机化装置,是一个装有大小、形状和质量完全相同的$${{5}{0}}$$个白球和$${{5}{0}}$$个红球的袋子.每个被调查者随机从袋中摸取$${{1}}$$个小球(摸出的球再放回袋中),摸到白球的居民如实回答第一个问题,摸到红球的居民如实回答第二个问题.如果在$${{3}{0}{0}}$$人中,共有$${{5}{8}}$$人回答了“是”,估计该地居民乱丢垃圾的概率为()
C
A.$$\frac{2 9} {1 5 0}$$
B.$$\frac{2 9} {7 5}$$
C.$$\frac{4} {7 5}$$
D.$$\frac{2 9} {1 0 0}$$
3、['随机事件发生的概率']正确率80.0%从一批准备出厂的电视机中随机抽取$${{1}{0}}$$台进行质量检查,其中有$${{1}}$$台是次品,若用$${{C}}$$表示抽到次品这一事件$${{.}}$$则下列说法中正确的是$${{(}{)}}$$
A.事件$${{C}}$$发生的概率为$$\frac{1} {1 0}$$
B.事件$${{C}}$$发生的频率为$$\frac{1} {1 0}$$
C.事件$${{C}}$$发生的概率接近$$\frac{1} {1 0}$$
D.每抽$${{1}{0}}$$台电视机,必有$${{1}}$$台次品
4、['事件的互斥与对立', '相互独立事件的概率', '随机事件发生的概率']正确率60.0%人民日报智慧媒体研究院在$${{2}{0}{2}{0}}$$智慧媒体高峰论坛上发布重磅智能产品——人民日报创作大脑,在$${{A}{I}}$$算法的驱动下,无论是图文编辑,视频编辑,还是素材制作,所有的优质内容创作都变得更加容易.已知某数据库有包括视频甲和图片乙在内的视频$${{a}}$$个、图片$${{b}}$$张$$( a, b \in\mathbf{N}^{*}, a > b > 1 ),$$从中随机选出一个视频和一张图片,记“视频甲和图片乙均入选”为事件$${{A}{,}}$$“视频甲入选”为事件$${{B}{,}}$$“图片乙入选”为事件$${{C}{,}}$$则$$P ( \bar{B} C )$$与$${{P}{(}{{B}{C}^{¯}}{)}}$$的大小关系是()
A
A.$$P ( \bar{B} C ) > P ( \bar{B} C )$$
B.$$P ( \bar{B} C )=P ( \bar{B} C )$$
C.$$P ( \bar{B} C ) < P ( \bar{B} C )$$
D.无法确定
5、['事件的互斥与对立', '随机事件发生的概率']正确率60.0%一个口袋中装有大小相同的$${{2}}$$个白球和$${{3}}$$个黑球,从中摸出一个球,放回后再摸出一个球,则两次摸出的球恰好颜色不同的概率为$${{(}{)}}$$
C
A.$$\frac{2} {5}$$
B.$$\frac{7} {1 2}$$
C.$$\frac{1 2} {2 5}$$
D.$$\frac{6} {2 5}$$
6、['随机事件发生的概率', '排列组合中的相邻与不相邻']正确率60.0%将$$A, ~ B, ~ C, ~ D$$这$${{4}}$$名同学从左至右随机地排成一排,则$${{“}{A}}$$与$${{B}}$$相邻且$${{A}}$$与$${{C}}$$之间恰好有$${{1}}$$名同学$${{”}}$$的概率是()
B
A.$$\frac{1} {2}$$
B.$$\frac{1} {4}$$
C.$$\frac{1} {6}$$
D.$$\frac{1} {8}$$
7、['事件的互斥与对立', '随机事件发生的概率']正确率60.0%下列说法正确的是()
D
A.抛一枚硬币$${{1}{0}}$$次,一定有$${{5}}$$次正面向上
B.明天本地降水概率为$${{7}{0}{%}}$$,是指本地下雨的面积是$${{7}{0}{%}}$$
C.互斥事件一定是对立事件,对立事件不一定是互斥事件
D.若$${{A}}$$与$${{B}}$$为互斥事件,则$$P ~ ( \textit{A} ) ~+P ~ ( \textit{B} ) ~ \leq1$$
8、['二项分布与n重伯努利试验', '随机事件发生的概率']正确率60.0%某彩票的中奖率为$$\frac{1} {3},$$买$${{3}}$$张此彩票,中奖的概率为 ()
B
A.$${{1}}$$
B.$$\frac{1 9} {2 7}$$
C.$$\frac{1 2} {2 7}$$
D.$$\frac{8} {2 7}$$
9、['方差与标准差', '随机事件发生的概率', '柱形图']正确率60.0%下图为某市$${{2}{0}{1}{7}}$$年$${{3}}$$月$${{2}{1}{∼}{{2}{7}}}$$日空气质量指数$${{(}{{A}{Q}{I}}{)}}$$柱形图,已知空气质量指数为$${{0}{∼}{{5}{0}}}$$空气质量属于优,$${{5}{1}{∼}{{1}{0}{0}}}$$空气质量属于良好,大于$${{1}{0}{0}}$$均属不同程度的污染.在这一周内,下列结论中正确的是()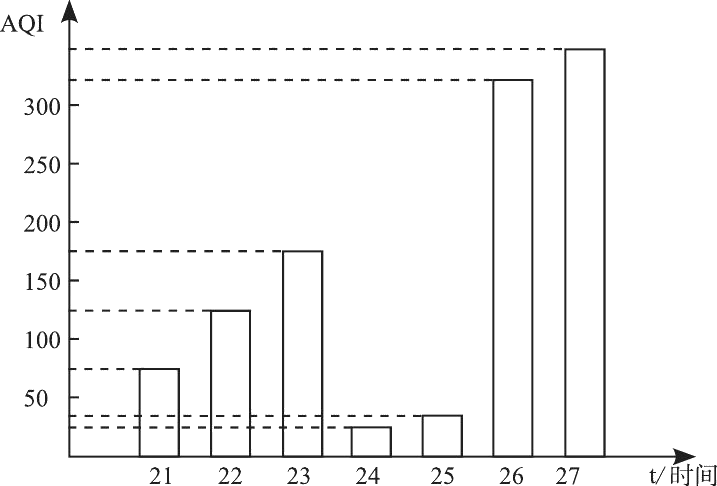
B
A.空气质量优良的概率为$$\begin{array} {l l} {5} \\ {\frac{5} {7}} \\ \end{array}$$
B.空气质量不是良好的天数为$${{6}}$$
C.这周的平均空气质量为良好
D.前三天$${{A}{Q}{I}}$$的方差大于后四天$${{A}{Q}{I}}$$的方差
10、['用频率估计概率', '概率的基本性质', '随机事件发生的概率']正确率60.0%某省高考数学试题中,共有$${{1}{2}}$$道选择题,每道选择题有$${{4}}$$个选项,其中只有$${{1}}$$个选项是正确的,即随机选择其中$${{1}}$$个选项正确的概率是$$\frac{1} {4}$$,某人说:“要是都不会做,每题都随机选择其中$${{1}}$$个选项,则一定有$${{3}}$$道题答对.”这个说法()
B
A.正确
B.错误
C.不一定
D.无法解释
1. 解析:
2. 解析:
3. 解析:
4. 解析:
5. 解析:
6. 解析:
7. 解析:
8. 解析:
9. 解析:
10. 解析:
.jpg)