正确率40.0%已知函数$$f ( x )=\left\{\begin{aligned} {} & {{}-\frac{1} {2} | x+2 |+1, x < 0,} \\ {} & {{} x^{3}, x > 0,} \\ \end{aligned} \right.$$若存在实数$$a, ~ b, ~ c,$$当$$a < b < c$$时,满足$$f ( a )=f ( b )=f ( c ),$$则$$a f ( a )+b f ( b )+c f ( c )$$的取值范围是()
B
A.$$(-4, 0 )$$
B.$$(-3, 0 )$$
C.$$[-4, 0 )$$
D.$$[-3, 0 )$$
2、['函数图象的识别', '同角三角函数的商数关系', '正弦函数图象的画法', '分段函数的图象']正确率60.0%函数$$y=| \operatorname{t a n} x | \cdot\operatorname{c o s} x ( 0 \leqslant x < \frac{3 \pi} {2}, x \neq\frac{\pi} {2} )$$的图象是$${{(}{)}}$$
D
A.
B.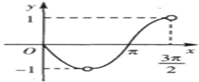
C.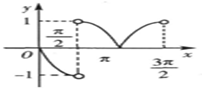
D.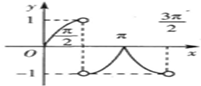
正确率40.0%设函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) \ =\left\{\begin{matrix} {a x^{2}+x, x \geq0} \\ {-a x^{2}+x, x < 0} \\ \end{matrix} \right.$$当$$x \in[-\frac{1} {2}, \ \frac{1} {2} ]$$时,恒有$$f \left( \begin{matrix} {x+a} \\ \end{matrix} \right) \ < f \left( \begin{matrix} {x} \\ \end{matrix} \right)$$,则实数$${{a}}$$的取值范围是()
C
A.$$( \frac{1-\sqrt{5}} {2}, \ \frac{1+\sqrt{5}} {2} )$$
B.$$( \mathrm{\ensuremath{-1}}, \mathrm{\ensuremath{\frac{1+\sqrt{5}} {2}}} )$$
C.$$( \frac{1-\sqrt{5}} {2}, \ 0 )$$
D.$$( ~ \frac{1-\sqrt{5}} {2}, ~-\frac{1} {2} ] ~$$
4、['导数的几何意义', '函数零点的概念', '分段函数的图象']正确率40.0%已知函数$$f \left( \begin{array} {c} {{x}} \\ {{x}} \end{array} \right)=\frac{1} {2}-\begin{array} {c} {{( \begin{array} {c} {x} \\ {-\sqrt{e}} \\ \end{array} )}} \\ {{( \begin{array} {c} {x} \\ {-\frac{1} {2}} \\ \end{array} )}} \end{array}$$其中$$x \in~ ( 0, ~+\infty) ~ ) ~, ~ g ~ ( x ) ~=l n x$$和函数$$h \sp{( x )}=\left\{\begin{matrix} {f ( x )} & {f ( x ) \geqslant g ( x )} \\ {g ( x )} & {f ( x ) < g ( x )} \\ \end{matrix} \right.$$,若方程$$h \textbf{\textit{( x )}}=k \textbf{x}$$有四个不同的解,则实数$${{k}}$$的取值范围是()
C
A.$$( 0, ~ \frac{1} {2} )$$
B.$$( 0, ~ \frac{\sqrt{e}} {2 e} )$$
C.$$( \frac{\sqrt{e}} {2 e}, \ \frac{1} {e} )$$
D.$$( \frac{1} {e}, \ \frac{\sqrt{e}} {e} )$$
5、['导数与最值', '根据函数零点个数求参数范围', '分段函数的图象']正确率60.0%已知函数$$f \left( x \right)=\left\{\begin{matrix} {2 x^{2}, x \leqslant0} \\ {e^{2 x}, x > 0} \\ \end{matrix} \right.$$,若方程$$\left[ f \left( x \right) \right]^{2}=a$$恰有两个不同的实数根$${{x}_{1}{,}{{x}_{2}}}$$,则$${{x}_{1}{+}{{x}_{2}}}$$的最大值是
B
A.$$- \frac{\sqrt2} 2$$
B.$$\operatorname{l n} \sqrt{2}-1$$
C.$$\operatorname{l n} 2-\sqrt{2}$$
D.$$\operatorname{l n} \sqrt{2}+1$$
6、['函数奇偶性的应用', '利用函数单调性求参数的取值范围', '分段函数与方程、不等式问题', '分段函数的图象']正确率40.0%已知函数$$f ( x )=\left\{\begin{array} {c} {-x^{2}+2 x, x > 0} \\ {0, x=0} \\ {x^{2}+m x, x < 0} \\ \end{array} \right.$$是奇函数,且在区间$$[-1, a-2 ]$$上满足任意的$$x_{1}, x_{2} ( x_{1} \neq x_{2} )$$,都有$$\frac{f ( x_{1} )-f ( x_{2} )} {x_{1}-x_{2}} > 0,$$则实数$${{a}}$$的取值范围是()
A
A.$$( 1, 3 )$$
B.$$[ 1, 3 )$$
C.$$( 1, 3 ]$$
D.
正确率40.0%已知定义在$${{R}}$$上的函数$${{f}{(}{x}{)}}$$满足$$f ( x )=\left\{\begin{aligned} {} & {{}-x^{2}-2, \, x \in(-1, \, 0 ]} \\ {} & {{} x^{2}-2, \, x \in( 0, \, 1 ]} \\ \end{aligned} \right.$$且$$f ( x+2 )=f ( x ), \, \, \, g ( x )=\frac{5-2 x} {x-2}$$,则方程$$f ( x )=g ( x )$$在区间$$[-3, \, 7 ]$$上的所有实根之和为()
C
A.$${{1}{4}}$$
B.$${{1}{2}}$$
C.$${{1}{1}}$$
D.$${{7}}$$
8、['函数奇偶性的应用', '函数奇、偶性的图象特征', '对数方程与对数不等式的解法', '分段函数的图象']正确率40.0%已知函数$$f \left( x \right)=\left\{\begin{matrix} {\operatorname{l g} x, ~ ~ ~ ~ ~ ~ ~ ~ x > 0} \\ {\operatorname{l g} \left(-\frac{1} {x} \right), ~ ~ x < 0} \\ \end{matrix} \right.$$,若$$f \left( m \right) > f \left(-m \right)$$,则实数$${{m}}$$的取值范围是()
A
A.$$(-1, 0 ) \bigcup\, ( 1,+\infty)$$
B.$$(-\infty,-1 ) \bigcup\, ( 1,+\infty)$$
C.$$(-1, 0 ) \bigcup\, ( 0, 1 )$$
D.$$(-\infty,-1 ) \bigcup\, ( 0, 1 )$$
9、['函数的周期性', '函数零点个数的判定', '分段函数的图象']正确率19.999999999999996%若函数$$y=\! f ( x ) ( x \! \in\! R )$$满足$$f ( x \!+\! 1 ) \!=\!-f ( x )$$,且$$x {\in} [-1, 1 ]$$时$$f ( x ) \!=\! 1 \!-\! x^{2}$$,函数$$g ( x ) \!=\! \left\{\begin{array} {c} {\operatorname{l g} x ( x \! > \! 0 )} \\ {-\frac{1} {x} ( x \! < \! 0 )} \\ \end{array} \right.$$,则函数$$h ( x )=f ( x )-g ( x )$$在区间$$[-5, 4 ]$$内的零点的个数为()
A
A.$${{7}}$$
B.$${{8}}$$
C.$${{9}}$$
D.$${{1}{0}}$$
10、['分段函数与方程、不等式问题', '根据函数零点个数求参数范围', '分段函数的图象']正确率40.0%设$$f \left( x \right)=\left\{\begin{matrix} {x+4, x \leqslant-2 \sharp x > 3} \\ {x^{2}-1,-2 < x < 3} \\ \end{matrix} \right.$$,若函数$$y=f ( x )+k$$的图象与$${{x}}$$轴恰有三个不同交点,则$${{k}}$$的取值范围是()
D
A.$$(-2, 1 )$$
B.$$[ 0, 1 ]$$
C.$$[-2, 0 )$$
D.$$[-2, 1 )$$
1. 解析:
2. 解析:
3. 解析:
4. 解析:
5. 解析:
6. 解析:
7. 解析:
8. 解析:
9. 解析:
10. 解析:
.jpg)