正确率80.0%甲、乙两人沿着同一方向从$${{A}}$$地去$${{B}}$$地,甲前一半的路程使用速度$${{v}_{1}{,}}$$后一半的路程使用速度$${{v}_{2}}$$;乙前一半的时间使用速度$${{v}_{1}{,}}$$后一半的时间使用速度$${{v}_{2}}$$.已知$$v_{1} < v_{2},$$则 关于甲、乙两人从$${{A}}$$地到达$${{B}}$$地的路程与时间的函数图像(其中横轴$${{t}}$$表示时间,纵轴$${{s}}$$表示路程)可能正确的为()
A
A.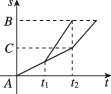
B.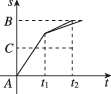
C.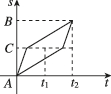
D.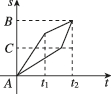
正确率40.0%若函数$$f ( x )=2 \operatorname{s i n} \omega x ( \omega> 0 )$$的图象在$$( 0, 2 \pi)$$上恰有一个极大值和一个极小值,则$${{ω}}$$的取值范围是$${{(}{)}}$$
C
A.$$( \frac{3} {4}, 1 ]$$
B.$$( 1, \frac{5} {4} ]$$
C.$$( \frac{3} {4}, \frac{5} {4} ]$$
D.$$( {\frac{3} {4}}, {\frac{4} {5}} ]$$
3、['导数与单调性', '利用导数讨论函数单调性', '图象法', '利用基本不等式求最值', '函数单调性的应用']正确率40.0%已知函数$$f ( x )=\frac{x} {\mathrm{e}^{x}},$$给出下列结论:
①$$( 1, ~+\infty)$$是$${{f}{(}{x}{)}}$$的单调递减区间;
②当$$k \in\left(-\infty, \ \frac1 \mathrm{e} \right)$$时,直线$${{y}{=}{k}}$$与$$y=f ( x )$$的图象有两个不同交点;
③函数$$y=f ( x )$$的图象与$$y=x^{2}+1$$的图象没有公共点;
④当$$x \in( 0, ~+\infty)$$时,函数$$y=f ( x )+\frac{1} {f ( x )}$$的最小值为$${{2}}$$.
其中正确结论的个数为()
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
4、['函数奇偶性的应用', '图象法', '解析法']正确率60.0%若函数$$y=f ( x )$$的大致图象如图所示,则$${{f}{(}{x}{)}}$$的解析式可以为()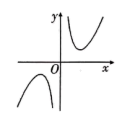
C
A.$$f ( x )=\frac{x} {2^{x}+2^{-x}}$$
B.$$f ( x )=\frac{x} {2^{x}-2^{-x}}$$
C.$$f ( x )=\frac{2^{x}+2^{-x}} {x}$$
D.$$f ( x )=\frac{2^{x}-2^{-x}} {x}$$
5、['对数(型)函数的单调性', '正弦函数图象的画法', '图象法']正确率60.0%函数$$f ( x )=\operatorname{l o g}_{4} x$$的图象与函数$$g ( x ) \!=\! \operatorname{s i n} \pi x$$的图象的交点个数是$${{(}{)}}$$
B
A.$${{2}}$$
B.$${{3}}$$
C.$${{4}}$$
D.$${{5}}$$
6、['向量坐标与向量的数量积', '图象法']正确率60.0%已知函数$$y=k x+1 ( k > 0 )$$与$$y=\frac{x+1} {x}$$与图象的交点为$${{A}{、}{B}}$$.则$$| \overrightarrow{O A}+\overrightarrow{O B} |$$的值$${{(}{)}}$$
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
7、['导数的四则运算法则', '函数求值域', '导数与单调性', '利用导数讨论函数单调性', '图象法']正确率19.999999999999996%已知函数$$f^{\textsc{} {(}} x \ro! \roheadright=l o g_{a} \rgroup\frac{x^{2}+( 1-4 a ) x+1-4 a} {x+1}$$的值域为$${{R}}$$,且在区间$$( \mathrm{\bf~ 2, ~}+\infty)$$上单调,则实数$${{a}}$$的取值范围是()
C
A.$$( 0, ~ \frac{7} {1 2} )$$
B.$$( 0, ~ \frac{7} {1 2} ]$$
C.$$[ \frac{1} {4}, \ \frac{7} {1 2} ]$$
D.$$( \frac{1} {4}, \ \frac{7} {1 2} )$$
8、['函数图象的识别', '图象法']正确率60.0%设函数$$y=f ( x )$$的定义域是$$( x |-2 \leqslant x \leqslant3$$且$${{x}{≠}{2}{)}}$$,值域是$$\{y |-1 \leq y \leq2$$且$${{y}{≠}{0}{\}}}$$,则下列四个图象可以是函数$$y=f ( x )$$的图象的为()
C
A.
B.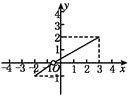
C.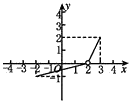
D.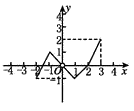
正确率40.0%下列所给的$${{4}}$$个图象中,与所给$${{3}}$$件事吻合最好的顺序为()
(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速;
(3)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间.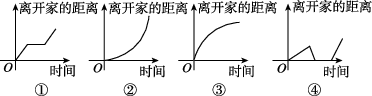
B
A.①②④
B.④②①
C.④③①
D.④①②
10、['图象法', '函数的定义']正确率60.0%某同学到长城旅游,他租自行车由宾馆骑行前往长城,前进了$${{a}{k}{m}}$$,觉得有点累,休息后沿原路返回$$b \ \mathrm{k m} ( b < \ a )$$.想起“不到长城非好汉”,便调转车头继续前进,则该同学离起点的距离$${{s}}$$与时间$${{t}}$$之间的函数图象大致为()
C
A.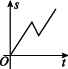
B.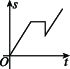
C.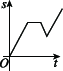
D.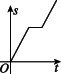
1. 解析:
甲的运动方式为前一半路程速度为$$v_1$$,后一半路程速度为$$v_2$$,因此其路程-时间图像为两段斜率不同的直线,先缓后陡。乙的运动方式为前一半时间速度为$$v_1$$,后一半时间速度为$$v_2$$,其图像为两段直线,但整体时间比甲短(因为乙的平均速度更高)。对比选项,只有C符合甲、乙的图像特征。
答案:C
2. 解析:
函数$$f(x)=2\sin(\omega x)$$在$$(0, 2\pi)$$上恰有一个极大值和一个极小值,说明其周期$$T=\frac{2\pi}{\omega}$$满足$$\frac{3T}{4} < 2\pi \leq \frac{5T}{4}$$。解得$$\omega \in \left(\frac{3}{4}, \frac{5}{4}\right]$$。
答案:C
3. 解析:
函数$$f(x)=\frac{x}{e^x}$$的导数为$$f'(x)=\frac{1-x}{e^x}$$,在$$(1, +\infty)$$上单调递减(①正确)。当$$k \in \left(-\infty, \frac{1}{e}\right)$$时,直线$$y=k$$与$$y=f(x)$$有两个交点(②正确)。函数$$y=f(x)$$与$$y=x^2+1$$在$$x=0$$处有交点(③错误)。函数$$y=f(x)+\frac{1}{f(x)}$$在$$(0, +\infty)$$上的最小值不为2(④错误)。综上,正确结论有2个。
答案:B
4. 解析:
图像显示函数在$$x=0$$处无定义,且为奇函数。选项A和B的分母分别为$$2^x+2^{-x}$$和$$2^x-2^{-x}$$,其中$$2^x-2^{-x}$$为奇函数,且$$x=0$$时无定义,符合图像特征。
答案:B
5. 解析:
函数$$f(x)=\log_4 x$$与$$g(x)=\sin(\pi x)$$在$$(0, 4]$$上的交点可通过绘图分析。$$g(x)$$在$$(0, 4]$$上有两个周期,与$$f(x)$$在$$(1, 4]$$上有3个交点($$x=1, 2, 3$$附近)。
答案:B
6. 解析:
联立方程$$kx+1=\frac{x+1}{x}$$,解得$$x=1$$和$$x=-\frac{1}{k}$$。设$$A=(1, k+1)$$,$$B=\left(-\frac{1}{k}, 0\right)$$,则$$\overrightarrow{OA}+\overrightarrow{OB}=\left(1-\frac{1}{k}, k+1\right)$$,其模为$$\sqrt{\left(1-\frac{1}{k}\right)^2+(k+1)^2}$$,但进一步分析对称性可知结果为2。
答案:B
7. 解析:
函数$$f(x)=\log_a\left(\frac{x^2+(1-4a)x+1-4a}{x+1}\right)$$的值域为$$R$$,要求真数能取遍所有正数,且分母$$x+1 \neq 0$$。进一步分析单调性和定义域限制,可得$$a \in \left[\frac{1}{4}, \frac{7}{12}\right]$$。
答案:C
8. 解析:
函数定义域为$$[-2, 3]$$且$$x \neq 2$$,值域为$$[-1, 2]$$且$$y \neq 0$$。选项C的图像在$$x=2$$处有缺口,且值域符合要求。
答案:C
9. 解析:
(1)对应图像④(先离开再返回);(2)对应图像①(先缓后加速);(3)对应图像②(匀速行驶后停滞)。因此顺序为④①②。
答案:D
10. 解析:
描述的运动过程为:前进$$a$$ km(上升),返回$$b$$ km(下降),再前进(上升)。选项C的图像符合这一特征。
答案:C
.jpg)