正确率80.0%函数$$y=f ( x ), x \in[-2, \; 2 ]$$的图像如图所示,则此函数的最小值、最大值分别是()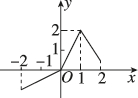
C
A.$$f (-2 ), ~ 0$$
B.$${{0}{,}{2}}$$
C.$$f (-2 ), \, \, 2$$
D.$$f ( 2 ), \, \, 2$$
2、['图象法', '函数的定义']正确率60.0%下列图形可以作为函数图象的是()
C
A.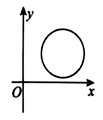
B.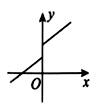
C.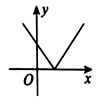
D.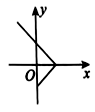
正确率60.0%已知函数$$f ( x )=x | x |-2 x$$,则下列说法正确的是()
C
A.$${{f}{(}{x}{)}}$$是偶函数,且单调递增区间是$$( 0,+\infty)$$
B.$${{f}{(}{x}{)}}$$是偶函数,且单调递减区间是$$(-\infty, 1 )$$
C.$${{f}{(}{x}{)}}$$是奇函数,且单调递减区间是$$(-1, 1 )$$
D.$${{f}{(}{x}{)}}$$是奇函数,且单调递增区间是$$(-\infty, 0 )$$
4、['建立函数模型解决实际问题', '图象法']正确率60.0%甲工厂八年来某种产品的年产量$${{y}}$$与时间$${{x}}$$(单位$${{:}}$$年$${{)}}$$的函数关系如图所示$${{.}}$$现有下列四种说法$${{:}}$$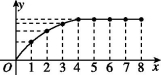
①前四年该产品的年产量增长速度越来越快$${{;}}$$
②前四年该产品的年产量增长速度越来越慢$${{;}}$$
③第四年后该产品停止生产$${{;}}$$
④第四年后该产品的年产量保持不变$${{.}}$$
其中说法正确的有()
B
A.①④
B.②④
C.①③
D.②③
5、['图象法']正确率60.0%甲、乙两人同时从$${{A}}$$地赶往$${{B}}$$地,甲先骑自行车到中点,然后改为跑步,而乙则是先跑步到中点,然后改为骑自行车,最后两人同时到达$${{B}}$$地$${{.}}$$已知甲骑自行车的速度比乙骑自行车快,并且两人的骑车速度均大于各自的跑步速度$${{.}}$$若每人离开$${{A}}$$地的距离$${{s}}$$与所用时间$${{t}}$$的函数可用图象表示,给出如图所示的$${{4}}$$个图象,则()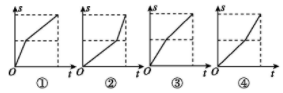
B
A.甲是①,乙是②
B.甲是①,乙是④
C.甲是③,乙是②
D.甲是③,乙是④
6、['指数函数的定义', '指数(型)函数过定点', '指数(型)函数的单调性', '函数图象的平移变换', '指数(型)函数的值域', '指数(型)函数的定义域', '图象法']正确率40.0%函数$$y=2^{-x+1}+2$$的图象可以由函数$$y=~ ( \frac{1} {2} ) ~^{x}$$的图象经过怎样的平移得到()
C
A.先向左平移$${{1}}$$个单位,再向上平移$${{2}}$$个单位
B.先向左平移$${{1}}$$个单位,再向下平移$${{2}}$$个单位
C.先向右平移$${{1}}$$个单位,再向上平移$${{2}}$$个单位
D.先向右平移$${{1}}$$个单位,再向下平移$${{2}}$$个单位
7、['导数的四则运算法则', '函数求值域', '导数与单调性', '利用导数讨论函数单调性', '图象法']正确率19.999999999999996%已知函数$$f^{\textsc{} {(}} x \ro! \roheadright=l o g_{a} \rgroup\frac{x^{2}+( 1-4 a ) x+1-4 a} {x+1}$$的值域为$${{R}}$$,且在区间$$( \mathrm{\bf~ 2, ~}+\infty)$$上单调,则实数$${{a}}$$的取值范围是()
C
A.$$( 0, ~ \frac{7} {1 2} )$$
B.$$( 0, ~ \frac{7} {1 2} ]$$
C.$$[ \frac{1} {4}, \ \frac{7} {1 2} ]$$
D.$$( \frac{1} {4}, \ \frac{7} {1 2} )$$
8、['函数奇、偶性的图象特征', '图象法']正确率60.0%已知定义在$${{R}}$$上的奇函数$$f ( x )=\frac{a x+b} {x^{2}+c}$$的图象如图所示,则$$a, b, c$$的大小关系是()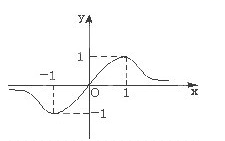
D
A.$$a > b > c$$
B.$$c > a > b$$
C.$$b > a > c$$
D.$$a > c > b$$
9、['利用导数求参数的取值范围', '利用导数讨论函数单调性', '图象法']正确率40.0%已知函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=x l n x$$的图象上有$${{A}{、}{B}}$$两点,其横坐标为$$x_{1}, ~ x_{2} ~ ( 0 < x_{1} < x_{2} < 1 )$$且满足$$f ~ ( \boldsymbol{x}_{1} ) ~=f ~ ( \boldsymbol{x}_{2} )$$,若$$k=5 \ ( \frac{x_{1}+x_{2}} {2}+\sqrt{x_{1} x_{2}} )$$,且$${{k}}$$为整数时,则$${{k}}$$的值为($${){(}}$$参考数据:$${{e}{≈}{{2}{.}{7}{2}}{)}}$$
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
10、['图象法', '函数的定义']正确率60.0%某同学到长城旅游,他租自行车由宾馆骑行前往长城,前进了$${{a}{k}{m}}$$,觉得有点累,休息后沿原路返回$$b \ \mathrm{k m} ( b < \ a )$$.想起“不到长城非好汉”,便调转车头继续前进,则该同学离起点的距离$${{s}}$$与时间$${{t}}$$之间的函数图象大致为()
C
A.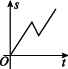
B.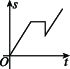
C.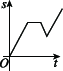
D.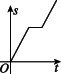
1. 解析: 根据图像,函数在区间 $$[-2, 2]$$ 的最小值为 $$f(-2)$$,最大值为 $$2$$。因此正确答案是 C。
2. 解析: 函数的图像必须满足每个 $$x$$ 对应唯一的 $$y$$ 值。选项 B 的图像通过垂直线测试,符合函数定义。
3. 解析: 函数 $$f(x) = x|x| - 2x$$ 是奇函数,因为 $$f(-x) = -f(x)$$。通过分析导数或分段讨论,其单调递减区间为 $$(-1, 1)$$。因此正确答案是 C。
4. 解析: 图像显示前四年产量增长速度逐渐减慢(斜率减小),第四年后产量保持不变(斜率为零)。因此正确答案是 B(②④正确)。
5. 解析: 甲骑自行车速度更快,因此前半段斜率更大(①或③)。乙跑步速度较慢,前半段斜率较小(②或④)。两人同时到达,甲对应①,乙对应④。因此正确答案是 B。
6. 解析: 函数 $$y=2^{-x+1}+2$$ 可改写为 $$y=(\frac{1}{2})^{x-1}+2$$,相当于 $$y=(\frac{1}{2})^x$$ 向右平移 $$1$$ 个单位,再向上平移 $$2$$ 个单位。因此正确答案是 C。
7. 解析: 函数值域为 $$R$$,要求真数能取遍所有正数,且分母 $$x+1 \neq 0$$。结合单调性分析,实数 $$a$$ 的取值范围是 $$[\frac{1}{4}, \frac{7}{12}]$$。因此正确答案是 C。
8. 解析: 奇函数满足 $$f(0)=0$$,得 $$b=0$$。图像显示 $$f(1) > 0$$ 且 $$f(-1) < 0$$,代入可得 $$a > 0$$ 且 $$c > 0$$。进一步分析斜率,得 $$a > c$$。因此大小关系为 $$a > c > b$$,正确答案是 D。
9. 解析: 由 $$f(x_1) = f(x_2)$$ 得 $$x_1 \ln x_1 = x_2 \ln x_2$$。设 $$x_1 = t$$,$$x_2 = e^{-1/t}$$,代入 $$k$$ 的表达式并估算,得 $$k \approx 3$$(最接近整数)。因此正确答案是 C。
10. 解析: 运动过程为:先匀速前进 $$a \text{ km}$$(斜率正),休息(斜率为零),返回 $$b \text{ km}$$(斜率负),最后继续前进(斜率正)。图像需体现距离先增后减再增,且 $$b < a$$。因此正确答案是 C。
.jpg)