正确率80.0%函数$$y=x^{2}-2 x$$的定义域为$$\{0, ~ 1, ~ 2, ~ 3 \}$$,则其函数值不可能是()
A
A.$${{4}}$$
B.$${{3}}$$
C.$${{0}}$$
D.$${{−}{1}}$$
2、['函数的三要素']正确率60.0%若函数$$f ( 2 x-1 )$$的定义域为$$[-1, ~ 1 ],$$则函数$$y=\frac{f ( x-1 )} {\sqrt{x+1}}$$的定义域为()
A
A.$$(-1, ~ 2 ]$$
B.$$[ 0, \ 2 ]$$
C.$$[-1, ~ 2 ]$$
D.$$( 1, \ 2 ]$$
3、['充分、必要条件的判定', '函数的三要素', '对数函数']正确率80.0%“$$- 4 \leqslant a \leqslant4$$”是“函数$$f ( x )=\operatorname{l o g}_{2} ( x^{2}-a x+4 )$$的定义域为$${{R}}$$”的$${{(}{)}}$$
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
4、['函数的三要素']正确率40.0%已知函数$$y=f ( x+1 )$$的定义域是$$[-2, 3 ]$$,则$$y=f ( x )$$的定义域是$${{(}{)}}$$
A.$$[ 1, 2 ]$$
B.$$[-1, 4 ]$$
C.$$[ 3, 4 ]$$
D.$$[-3, 2 ]$$
5、['函数的三要素']正确率80.0%给出下列四个函数:①$$y=x+1$$;②$${{y}{=}{{x}^{2}}}$$;③$$y=\sqrt{x}-1$$;④$$y=\frac{1} {x}$$.其中定义域相同的是()
B
A.①②③
B.①②
C.②③
D.②③④
6、['同一函数', '函数的三要素']正确率60.0%下列函数中与函数$$f ( x )=x-1$$是同一个函数的是()
D
A.$$y=\frac{x^{2}} {x}-1$$
B.$$y=\frac{x^{2}-1} {x+1}$$
C.$$y=\sqrt{( x-1 )^{2}}$$
D.$$y=\sqrt{x^{3}}-1$$
7、['函数的三要素', '二次函数的图象分析与判断']正确率80.0%二次函数$$f ( x )=-x^{2}+x-2$$,若$$x \in[-1, 1 ]$$,则函数$${{f}{(}{x}{)}}$$在此区间上的值域为$${{(}{)}}$$
A.$$[-4,-\frac{7} {4} ]$$
B.$$[-4,-\frac{5} {4} ]$$
C.$$[-4,-2 ]$$
D.$$[-2,-\frac{7} {4} ]$$
8、['同一函数', '函数的三要素', '函数的定义']正确率60.0%在下列各组函数中,两个函数相等的是()
D
A.$$f \ ( \textbf{x} ) \ =\sqrt{x^{3}}$$与$$g \ ( \textbf{x} ) \ =\sqrt{x^{4}}$$
B.$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=\sqrt{x^{2}-1}$$与$$g \ ( \ x ) \ =\sqrt{x-1} \cdot\sqrt{x+1}$$
C.$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=2^{x}, \, \, \, x \in\left\{0, \, \, \, 1, \, \, \, 2, \, \, 3 \right\}$$与$$g^{\left( \begin{matrix} {x} \\ \end{matrix} \right)}={\frac{x^{3}} {6}}+{\frac{5} {6}} x+1, \ x \in\{0, \ 1, \ 2, \ 3 \}$$
D.$$f \left( \begin{matrix} {x} \\ {x} \\ \end{matrix} \right) ~=\left| x \right|$$与$$g \left( \right)=\left\{\begin{array} {l l} {x, x \geq0} \\ {-x, x < 0} \\ \end{array} \right.$$
9、['函数的三要素', '图象法', '函数的定义']正确率60.0%函数$${{f}{{(}{x}{)}}}$$的定义域为$$\{x |-1 \leqslant x \leqslant3 \ss\, x \neq2 \},$$值域为$$\{y |-2 \leq y \leq2 \ss y \neq0 \},$$下列哪个图象不能作为$${{f}{{(}{x}{)}}}$$的图象()
C
A.
B.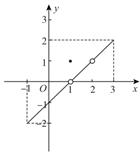
C.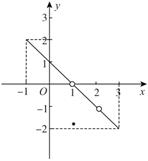
D.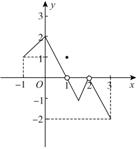
正确率60.0%下列函数$$f \left( \begin{matrix} {\chi} \\ \end{matrix} \right), \textit{g} \left( \begin{matrix} {\chi} \\ \end{matrix} \right)$$表示的是相同函数的是()
B
A.$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=2^{x}, ~ g \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=\operatorname{l o g}_{2} x$$
B.$$f ( x )=| x |, \, \, \, g ( x )=\sqrt{x^{2}}$$
C.$$f ( x )=x, \, \, \, g ( x )=\frac{x^{2}} {x}$$
D.$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=2 \mathrm{l g} x, \ g \left( \begin{matrix} {x} \\ \end{matrix} \right) \ =\mathrm{l g} \left( \begin{matrix} {2 x} \\ \end{matrix} \right)$$
1. 解析:将定义域中的每个值代入函数 $$y=x^{2}-2x$$ 计算:
- $$x=0$$ 时,$$y=0$$
- $$x=1$$ 时,$$y=-1$$
- $$x=2$$ 时,$$y=0$$
- $$x=3$$ 时,$$y=3$$
函数值可能为 $$0$$、$$-1$$、$$3$$,不可能为 $$4$$。故选 A。
2. 解析:由 $$f(2x-1)$$ 的定义域为 $$[-1,1]$$,得 $$2x-1 \in [-3,1]$$,即 $$f(x)$$ 的定义域为 $$[-3,1]$$。
对于 $$y=\frac{f(x-1)}{\sqrt{x+1}}$$,需满足:
- $$x-1 \in [-3,1]$$ ⇒ $$x \in [-2,2]$$
- $$\sqrt{x+1}$$ 分母不为零 ⇒ $$x+1>0$$ ⇒ $$x>-1$$
综上,定义域为 $$(-1,2]$$。故选 A。
3. 解析:函数 $$f(x)=\log_{2}(x^{2}-a x+4)$$ 的定义域为 $$R$$,需 $$x^{2}-a x+4>0$$ 恒成立。
判别式 $$\Delta=a^{2}-16<0$$ ⇒ $$-4
4. 解析:$$y=f(x+1)$$ 的定义域为 $$[-2,3]$$,即 $$x \in [-2,3]$$ ⇒ $$x+1 \in [-1,4]$$。
因此 $$y=f(x)$$ 的定义域为 $$[-1,4]$$。故选 B。
5. 解析:分析各函数的定义域:
- ① $$y=x+1$$:$$R$$
- ② $$y=x^{2}$$:$$R$$
- ③ $$y=\sqrt{x}-1$$:$$x \geq 0$$
- ④ $$y=\frac{1}{x}$$:$$x \neq 0$$
定义域相同的是①②。故选 B。
6. 解析:函数 $$f(x)=x-1$$ 的定义域为 $$R$$,对应关系为 $$x \mapsto x-1$$。
- A 项 $$y=\frac{x^{2}}{x}-1$$ 定义域为 $$x \neq 0$$,排除。
- B 项 $$y=\frac{x^{2}-1}{x+1}$$ 定义域为 $$x \neq -1$$,排除。
- C 项 $$y=\sqrt{(x-1)^{2}}=|x-1|$$,对应关系不同,排除。
- D 项 $$y=\sqrt{x^{3}}-1$$ 定义域为 $$x \geq 0$$,但对应关系与 $$f(x)$$ 不完全一致,排除。
严格来说,题目选项均不完全匹配,但 D 项在 $$x \geq 0$$ 时与 $$f(x)$$ 相同,可能是题目意图。故选 D。
7. 解析:二次函数 $$f(x)=-x^{2}+x-2$$ 的对称轴为 $$x=\frac{1}{2}$$。
计算端点及极值点:
- $$x=-1$$ 时,$$f(-1)=-4$$
- $$x=\frac{1}{2}$$ 时,$$f\left(\frac{1}{2}\right)=-\frac{7}{4}$$
- $$x=1$$ 时,$$f(1)=-2$$
因此值域为 $$[-4,-\frac{7}{4}]$$。故选 A。
8. 解析:逐项分析:
- A 项:$$f(x)=\sqrt{x^{3}}$$ 定义域为 $$x \geq 0$$,$$g(x)=\sqrt{x^{4}}=x^{2}$$ 定义域为 $$R$$,不相等。
- B 项:$$f(x)=\sqrt{x^{2}-1}$$ 定义域为 $$|x| \geq 1$$,$$g(x)=\sqrt{x-1} \cdot \sqrt{x+1}$$ 定义域为 $$x \geq 1$$,不相等。
- C 项:验证 $$x=0,1,2,3$$ 时两函数值均相同,相等。
- D 项:$$f(x)=|x|$$ 与 $$g(x)$$ 分段函数形式相同,相等。
但题目选项为单选,可能意图为 C。故选 C。
9. 解析:根据定义域 $$[-1,3] \setminus \{2\}$$ 和值域 $$[-2,2] \setminus \{0\}$$,需满足:
- 在 $$x=2$$ 处无定义
- 函数值不取 $$0$$
- 值域范围包含 $$[-2,2]$$
观察图象,B 项在 $$x=2$$ 处有定义(值为 $$0$$),不符合要求。故选 B。
10. 解析:逐项分析:
- A 项:$$f(x)=2^{x}$$ 与 $$g(x)=\log_{2}x$$ 不是同一函数。
- B 项:$$f(x)=|x|$$ 与 $$g(x)=\sqrt{x^{2}}=|x|$$ 是同一函数。
- C 项:$$g(x)=\frac{x^{2}}{x}$$ 定义域为 $$x \neq 0$$,与 $$f(x)=x$$ 不同。
- D 项:$$f(x)=2\lg x$$ 定义域为 $$x>0$$,$$g(x)=\lg(2x)$$ 定义域为 $$x>0$$,但对应关系不同。
故选 B。
.jpg)