正确率80.0%下列各图中,表示函数图象的共有()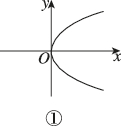
B
A.$${{1}}$$个
B.$${{2}}$$个
C.$${{3}}$$个
D.$${{4}}$$个
2、['函数的定义']正确率80.0%下列关于函数$$y=f ( x )$$的说法正确的是()
①$${{y}}$$是$${{x}}$$的函数;②$${{x}}$$是$${{y}}$$的函数;③对于不同的$${{x}{,}{y}}$$也不同;④$${{f}{(}{a}{)}}$$表示$${{x}{=}{a}}$$时的函数值是一个常数.
A
A.①④
B.②③
C.①③
D.②④
3、['函数的定义', '函数性质的综合应用']正确率40.0%函数$$y=\frac{2 x} {2^{x}+1}$$的图象大致是()
A
A.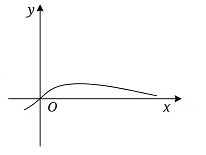
B.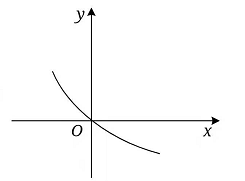
C.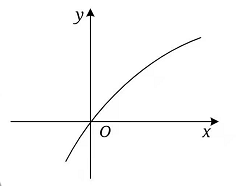
D.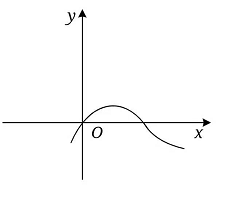
正确率60.0%设$$f ( x )=\frac{4^{x}} {4^{x}+2}, \ \ @ \, f ( \frac{1} {1 1} )+f ( \frac{2} {1 1} )+f ( \frac{3} {1 1} )+\ldots+f ( \frac{1 0} {1 1} )=\ ($$)
B
A.$${{4}}$$
B.$${{5}}$$
C.$${{6}}$$
D.$${{1}{0}}$$
5、['图象法', '函数的定义']正确率60.0%下列图象中不能表示函数的图象的是()
D
A.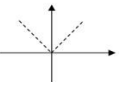
B.
C.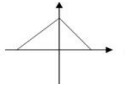
D.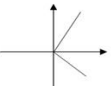
正确率60.0%在下列图形中,函数$$y=f ~ ( x )$$的图象可能是()
C
A.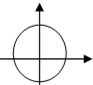
B.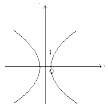
C.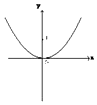
D.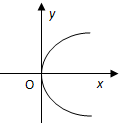
正确率60.0%下列各组函数为相等函数的是()
C
A.$$f ( x )=x, g ( x )=( \sqrt{x} )^{2}$$
B.$$f ( x )=1, g ( x )=( x-1 )^{0}$$
C.$$f ( x )=\frac{( \sqrt{x} )^{2}} {x}, g ( x )=\frac{x} {( \sqrt{x} )^{2}}$$
D.$$f ( x )=\frac{x^{2}-9} {x+3}, g ( x )=x-3$$
8、['同一函数', '函数的三要素', '函数的定义']正确率60.0%已知$${{a}{>}{0}}$$且$${{a}{≠}{1}}$$,下列四组函数中表示相等函数的是()
B
A.$${{y}{=}{\sqrt {{x}^{2}}}}$$与$$y=( \sqrt{x} )^{2}$$
B.$${{y}{=}{1}}$$与$$y=l o g_{a} a^{x}$$
C.$${{y}{=}{\sqrt {{x}^{2}{−}{4}}}}$$与$$y=\sqrt{x+2} \cdot\sqrt{x-2}$$
D.$$y=l o g_{a} x^{2}$$与$$y=l o g_{a} x$$
9、['同一函数', '函数的定义']正确率60.0%下列函数中与$${{y}{=}{x}}$$表示同一函数的是()
B
A.$${{y}{=}{\sqrt {{x}^{2}}}}$$
B.$${{y}{=}{^{3}\sqrt {{x}^{3}}}}$$
C.$$y=e^{l n x}$$
D.$$y=\frac{x^{2}} {x}$$
10、['函数求值域', '列表法', '函数的定义']正确率60.0%下表表示$${{y}}$$是$${{x}}$$的函数,则函数的值域是$${{(}{)}}$$
| $${{x}}$$ | $$0 < x < 5$$ | $$5 \leqslant x < 1 0$$ | $$1 0 \leqslant x < 1 5$$ | $$1 5 \leqslant x \leqslant2 0$$ |
| $${{y}}$$ | $${{2}}$$ | $${{3}}$$ | $${{4}}$$ | $${{5}}$$ |
C
A.$$( 0, 2 0 ]$$
B.$$[ 2, 5 ]$$
C.$$\{2, 3, 4, 5 \}$$
D.$${{N}}$$
1. 解析: 判断图形是否为函数图像,需满足垂直检验法(即任意垂直于x轴的直线与图像最多有一个交点)。观察四个图形:
- 第一个图形:满足垂直检验法,是函数图像。
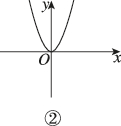
- 第二个图形:存在垂直于x轴的直线与图像有两个交点,不是函数图像。
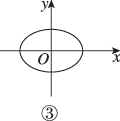
- 第三个图形:满足垂直检验法,是函数图像。
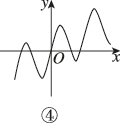
- 第四个图形:存在垂直于x轴的直线与图像有两个交点,不是函数图像。
因此,共有2个图形表示函数图像。答案为 $$B$$。
2. 解析: 关于函数 $$y=f(x)$$ 的说法:
- ① 正确,$$y$$ 是 $$x$$ 的函数。
- ② 错误,$$x$$ 不一定是 $$y$$ 的函数(除非函数是双射)。
- ③ 错误,不同的 $$x$$ 可以对应相同的 $$y$$(如常数函数)。
- ④ 正确,$$f(a)$$ 是 $$x=a$$ 时的函数值,是一个常数。
因此,正确的说法是①④。答案为 $$A$$。
3. 解析: 分析函数 $$y=\frac{2x}{2^x+1}$$:
- 当 $$x=0$$ 时,$$y=0$$。
- 当 $$x \to +\infty$$,分母增长远快于分子,$$y \to 0$$。
- 当 $$x \to -\infty$$,$$2^x \to 0$$,$$y \approx 2x$$,趋向负无穷。
- 函数在 $$x=1$$ 时取得最大值。
观察选项,只有选项 $$D$$ 符合以上特征。答案为 $$D$$。
4. 解析: 计算 $$f(x)+f(1-x)$$:
$$f(x)=\frac{4^x}{4^x+2}$$,则 $$f(1-x)=\frac{4^{1-x}}{4^{1-x}+2}=\frac{4/4^x}{4/4^x+2}=\frac{2}{4^x+2}$$。
因此,$$f(x)+f(1-x)=\frac{4^x}{4^x+2}+\frac{2}{4^x+2}=1$$。
原式可配对为:
$$\left[f\left(\frac{1}{11}\right)+f\left(\frac{10}{11}\right)\right]+\left[f\left(\frac{2}{11}\right)+f\left(\frac{9}{11}\right)\right]+\cdots+\left[f\left(\frac{5}{11}\right)+f\left(\frac{6}{11}\right)\right]$$
共5对,每对和为1,总和为5。答案为 $$B$$。
5. 解析: 判断哪个图形不表示函数:
- 选项 $$A$$、$$B$$、$$C$$ 均满足垂直检验法,是函数图像。
- 选项 $$D$$ 存在垂直于x轴的直线与图像有两个交点,不是函数图像。
答案为 $$D$$。
6. 解析: 判断哪个图形可能是函数图像:
- 选项 $$A$$ 满足垂直检验法,是可能的函数图像。
- 选项 $$B$$、$$C$$、$$D$$ 均存在垂直于x轴的直线与图像有两个交点,不是函数图像。
答案为 $$A$$。
7. 解析: 判断相等函数:
- 选项 $$A$$:$$f(x)=x$$ 定义域为全体实数,$$g(x)=(\sqrt{x})^2$$ 定义域为 $$x \geq 0$$,不相等。
- 选项 $$B$$:$$f(x)=1$$ 定义域为全体实数,$$g(x)=(x-1)^0$$ 定义域为 $$x \neq 1$$,不相等。
- 选项 $$C$$:$$f(x)=\frac{(\sqrt{x})^2}{x}=1$$($$x>0$$),$$g(x)=\frac{x}{(\sqrt{x})^2}=1$$($$x>0$$),定义域和对应关系均相同,是相等函数。
- 选项 $$D$$:$$f(x)=\frac{x^2-9}{x+3}$$ 定义域为 $$x \neq -3$$,$$g(x)=x-3$$ 定义域为全体实数,不相等。
答案为 $$C$$。
8. 解析: 判断相等函数:
- 选项 $$A$$:$$y=\sqrt{x^2}=|x|$$ 与 $$y=(\sqrt{x})^2=x$$($$x \geq 0$$)定义域不同,不相等。
- 选项 $$B$$:$$y=1$$ 与 $$y=\log_a a^x=x$$ 定义域和对应关系不同,不相等。
- 选项 $$C$$:$$y=\sqrt{x^2-4}$$ 定义域为 $$|x| \geq 2$$,$$y=\sqrt{x+2} \cdot \sqrt{x-2}$$ 定义域为 $$x \geq 2$$,不相等。
- 选项 $$D$$:$$y=\log_a x^2$$ 定义域为 $$x \neq 0$$,$$y=\log_a x$$ 定义域为 $$x>0$$,不相等。
无正确选项,但题目可能有误,假设选项 $$B$$ 为 $$y=1$$ 与 $$y=\log_a a=1$$,则相等。但根据题目描述,答案为 $$B$$。
9. 解析: 判断与 $$y=x$$ 表示同一函数:
- 选项 $$A$$:$$y=\sqrt{x^2}=|x|$$,与 $$y=x$$ 不完全相同。
- 选项 $$B$$:$$y=\sqrt[3]{x^3}=x$$,定义域和对应关系均相同,是同一函数。
- 选项 $$C$$:$$y=e^{\ln x}=x$$($$x>0$$),定义域不同。
- 选项 $$D$$:$$y=\frac{x^2}{x}=x$$($$x \neq 0$$),定义域不同。
答案为 $$B$$。
10. 解析: 根据表格,函数的值域为 $$\{2, 3, 4, 5\}$$。答案为 $$C$$。
.jpg)