正确率60.0%设$$f ( x )=\left\{\begin{cases} {-1 ( x > 0 ),} \\ {1 ( x < 0 ),} \\ \end{cases} \right.$$则$$\frac{( a+b )-( a-b ) \cdot f ( a-b )} {2} ( a \neq b )$$的值为()
D
A.$${{a}}$$
B.$${{b}}$$
C.$${{a}{,}{b}}$$中较小的数
D.$${{a}{,}{b}}$$中较大的数
2、['分段函数的定义', '分段函数的图象']正确率60.0%已知函数$$f ( x )=\left\{\begin{array} {l l} {x^{2}, x > 0,} \\ {1} & {g ( x )=-f (-x ),} \\ {{\frac{1} {x}}, x < 0,} & {} \\ \end{array} \right.$$则函数$${{g}{(}{x}{)}}$$的大致图像是()
D
A.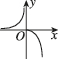
B.
C.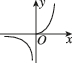
D.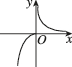
正确率40.0%已知函数$$f \sp{( \textbf{x} )}=\left\{\begin{array} {l} {l o g_{2} x, \ x > 1} \\ {( \frac{1} {2} ) \sp{x}, \ x \leq1} \\ \end{array} \right.$$,则)
A
A.$${{2}}$$
B.$${{−}{2}}$$
C.$$\frac{1} {2}$$
D.$$- \frac{1} {2}$$
4、['指数(型)函数的单调性', '单调性的定义与证明', '分段函数的定义']正确率60.0%已知函数$$f ( x )=\left\{\begin{array} {l} {( 1-5 a ) x-3 a, x < 0} \\ {a^{x}-2, x \geq0} \\ \end{array} \right. ( a > 0 )$$且$${{a}{≠}{1}{)}}$$满足$$\forall x_{1}, ~ x_{2} \in R, ~ ~ \frac{f ( x_{1} )-f ( x_{2} )} {x_{1}-x_{2}} < 0,$$则实数$${{a}}$$的取值范围是()
A
A.$$( \frac{1} {5}, ~ \frac{1} {3} ]$$
B.$$( 0, ~ \frac{1} {3} ]$$
C.$$( {\bf0}, \mathrm{\bf~ 1} )$$
D.$$( 0, ~ \frac{2} {3} ]$$
5、['已知函数值(值域)求自变量或参数', '分段函数的定义']正确率60.0%已知函数,$$f \left( x \right)=\left\{\begin{matrix} {x+3} & {\left( x < 1 \right)} \\ {x^{2}-2 x} & {\left( x \geq1 \right)} \\ \end{matrix} \right., \# f \left( m \right)=3$$,则$${{m}}$$的值为()
A
A.$${{0}}$$或$${{3}}$$
B.$${{−}{1}}$$或$${{3}}$$
C.$${{0}}$$或$${{−}{1}}$$
D.$${{0}}$$
6、['分段函数与方程、不等式问题', '分段函数求值', '分段函数的定义']正确率60.0%设函数$$f ( x )=\left\{\begin{array} {l} {{\frac{1} {2} x-1 ( x \geqslant0 )}} \\ {{\frac{1} {x} ( x < 0 )}} \\ \end{array} \right.$$,若$$f ( a )=a$$,则实数$${{a}}$$的值为$${{(}{)}}$$
D
A.$${{±}{1}}$$或$${{−}{2}}$$
B.$${{±}{1}}$$
C.$${{−}{2}}$$或$${{−}{1}}$$
D.$${{−}{1}}$$
7、['已知函数值(值域)求自变量或参数', '分段函数的定义']正确率60.0%设$$f \left( \begin{matrix} {x} \\ {x} \\ \end{matrix} \right)=\left\{\begin{matrix} {1, \ x > 0} \\ {0, \ x=0} \\ {-1, \ \ x < 0} \\ \end{matrix} \right., \ g \ ( \boldsymbol{x} )=\left\{\begin{matrix} {1, x \neq y+\operatorname* {m a x}_{\mathbb{K}}} \\ {0, x \neq y \in\mathbb{K}_{\mathbb{K}} \sharp\mathbb{K}_{\mathbb{K}}} \\ \end{matrix} \right.$$,若$$f \left( \textit{g} \left( \textbf{a} \right) \right) \ =0$$,则()
A
A.$${{a}}$$为无理数
B.$${{a}}$$为有理数
C.$${{a}{=}{0}}$$
D.$${{a}{=}{1}}$$
8、['函数求值域', '分段函数的定义']正确率40.0%函数$$f ( x )=\left\{\begin{matrix} {x^{2}-2 x+2, ( x > 0 )} \\ {3 x-f (-x ), ( x \leqslant0 )} \\ \end{matrix} \right.$$,则函数$${{f}{(}{x}{)}}$$的值域是()
D
A.$$(-\infty,+\infty)$$
B.$$(-\infty,-\frac{7} {4} ] \bigcup[ 1,+\infty)$$
C.$$(-\infty,-\frac{7} {4} ) \bigcup[ 1,+\infty)$$
D.$$(-\infty,-2 ) \bigcup[ 1,+\infty) \bigcup\{0 \}$$
9、['函数的对称性', '分段函数的定义', '分段函数的图象']正确率40.0%已知函数$$f ( x )=\left\{\begin{matrix} {| \operatorname{l o g}_{4} ( x+1 ) | \, (-1 < x < 1 )} \\ {\operatorname{c o s} \frac{\pi} {3} x ( 1 \leqslant x \leqslant6 )} \\ \end{matrix} \right.$$,若存在实数$$x_{1}, x_{2}, x_{3}, x_{4}$$,满足$$x_{1} < x_{2} < x_{3} < x_{4}$$且$$f ( x_{1} )=f ( x_{2} )=f ( x_{3} )=f ( x_{4} )$$,则$$\frac{( x_{3}-1 ) ( x_{4}-1 )} {( x_{1}+1 ) ( x_{2}+1 )}$$的范围是$${{(}{)}}$$
A
A.$$( 0, \frac{7} {4} )$$
B.$$( 0, \frac{7} {4} ]$$
C.$$( 1, 4 )$$
D.$$[ 1, 4 ]$$
10、['分段函数求值', '分段函数的定义']正确率80.0%已知$$f ( x )=\left\{\begin{aligned} {x^{2}+1, x < 1,} \\ {-2 x+3, x \geq1,} \\ \end{aligned} \right.$$则$$f [ f ( 2 ) ]=$$()
B
A.$${{−}{7}}$$
B.$${{2}}$$
C.$${{−}{1}}$$
D.$${{5}}$$
1. 解析:
2. 解析:
3. 解析:
4. 解析:
5. 解析:
6. 解析:
7. 解析:
8. 解析:
9. 解析:
10. 解析:
.jpg)