.jpg)
正确率40.0%已知定义在区间$$[ 0， \ 2 ]$$上的函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=l n \left( \begin{matrix} {2 e^{x}+3 x-a} \\ \end{matrix} \right)$$，若存在$$m \in[ 0， ~ 1 ]$$，使$$f \left( \textit{f} \left( \textbf{m} \right) \right) \ =\textit{m}$$成立，则$${{a}}$$的取值范围为（）
D
A.$$[ 1， ~ e+3 )$$
B.$$[ 1， ~ \frac{3} {2} )$$
C.$$[ 1， ~ e+2 )$$
D.$$[ 1， \ 2 )$$
2、['数列的递推公式'， '等比数列的通项公式'， '构造法求数列通项'， '函数单调性的判断'， '函数单调性的应用']正确率40.0%已知函数$$y=f ( x )$$的定义域为$$( 0，+\infty)$$，当$${{x}{>}{1}}$$时$$f ( x ) > 0$$，对任意的$$x， \， \， y \in( 0，+\infty)， \， \， \， f ( x )+f ( y )=f ( x \cdot y )$$成立，若数列$${{\{}{{a}_{n}}{)}}$$满足$$a_{1}=f ( 1 )$$，且$$f ( a_{n+1} )=f ( 2 a_{n}+1 )， \， \， \， n \in N^{*}$$，则$$a_{2 0 1 7}$$的值为$${{(}{)}}$$
C
A.$$2^{2 0 1 4}-1$$
B.$$2^{2 0 1 5}-1$$
C.$$2^{2 0 1 6}-1$$
D.$$2^{2 0 1 7}-1$$
3、['函数奇偶性的应用'， '利用函数单调性解不等式'， '绝对值不等式的解法'， '函数单调性的判断']正确率60.0%若偶函数$${{f}{{(}{x}{)}}}$$在区间$$[ 0 \;， \;+\infty)$$上单调增加，则满足$$f \left( 1-2 x \right) < f \left( \frac1 3 \right)$$的$${{x}}$$的取值范围是$${{(}{)}}$$
A
A.$$( {\frac{1} {3}}， {\frac{2} {3}} )$$
B.$$[ \frac{1} {3}， \ \frac{2} {3} )$$
C.$$( {\frac{1} {2}}， {\frac{2} {3}} )$$
D.$$[ \frac{1} {2}， \ \frac{2} {3} )$$
4、['函数单调性的判断']正确率60.0%若函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ( \begin{matrix} {x} \\ {x} \\ \end{matrix} \in R )$$对任意$${{x}_{1}{≠}{{x}_{2}}}$$，都有$$x_{1} f \， ( \， x_{1} \， ) \， \， \，+x_{2} f \， ( \， x_{2} \， ) \， \， \， > x_{1} f \， ( \， x_{2} \， ) \， \， \，+x_{2} f \， ( \， x_{1} \， )$$，则函数$${{f}{（}{x}{）}}$$是（）
A
A.增函数
B.减函数
C.奇函数
D.偶函数
5、['导数与极值'， '函数单调性的判断'， '函数的单调区间']正确率80.0%函数$$y=f ( x )$$导函数$$f^{\prime} ( x )$$的图象如图所示，则下列说法正确的是（）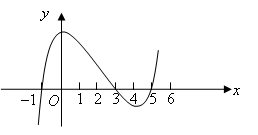
D
A.函数$$y=f ( x )$$在$$(-\infty， 0 )$$上单调递增
B.函数$$y=f ( x )$$的递减区间为$$( 3， 5 )$$
C.函数$$y=f ( x )$$在$${{x}{=}{0}}$$处取得极大值
D.函数$$y=f ( x )$$在$${{x}{=}{5}}$$处取得极小值
6、['函数零点所在区间的判定'， '函数单调性的判断'， '函数零点存在定理']正确率40.0%函数$$f \mid x \mid=( \frac{1} {3} )^{x}-\sqrt{x}$$的零点所在区间为（）
B
A.$$( 0， ~ \frac{1} {3} )$$
B.$$( \ \frac{1} {3}， \ \frac{1} {2} )$$
C.$$( \; \frac{1} {2}， \; \; 1 )$$
D.$$( 1， \ 2 )$$
7、['利用导数讨论函数单调性'， '函数单调性的判断']正确率60.0%下列函数中，在$$( 0，+\infty)$$内为增函数的是（$${）}$$．
B
A.$$f ( x )=\operatorname{s i n} \， 2 x$$
B.$$f ( x )=x e^{x}$$
C.$$f ( x )=x^{3}-x$$
D.$$f ( x )=-x+\operatorname{l n} \， x$$
8、['幂函数模型的应用'， '函数单调性的判断']正确率60.0%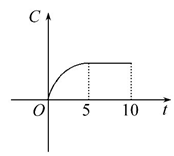
某工厂$${{1}{0}}$$
C
A.$${①{③}}$$
B.$${②{④}}$$
C.$${②{③}}$$
D.$${①{④}}$$
9、['函数单调性的判断']正确率60.0%下列函数中，在$$( \ -1， \ \ +\infty)$$上为减函数的是（）
D
A.$${{y}{=}{{3}^{x}}}$$
B.$$y=x^{2}-2 x+3$$
C.$${{y}{=}{x}}$$
D.$$y=-x^{2}-4 x+3$$
10、['函数奇、偶性的证明'， '函数单调性的判断']正确率40.0%下列函数中，与函数$${{f}{{(}{x}{)}}{=}{x}}$$的单调性与奇偶性都相同的是（）
D
A.$${{y}{=}{{s}{i}{n}}{x}}$$
B.$$y=x^{3}-x$$
C.$${{y}{=}{{2}^{x}}}$$
D.$$y=\operatorname{l g} \! \left( x+\sqrt{x^{2}+1} \right)$$
1. 题目解析：
2. 题目解析：
3. 题目解析：
4. 题目解析：
5. 题目解析：
- 在 $$(-\infty, 0)$$ 上 $$f'(x) > 0$$，函数单调递增，A 正确。
- 在 $$(3, 5)$$ 上 $$f'(x) < 0$$，函数单调递减，B 正确。
- 在 $$x = 0$$ 处 $$f'(x)$$ 由正变正，不是极值点，C 错误。
- 在 $$x = 5$$ 处 $$f'(x)$$ 由负变正，是极小值点，D 正确。
故选 ABD，但题目为单选题，可能是图像描述不清导致。
6. 题目解析：
- $$f(0) = 1 > 0$$，$$f\left(\frac{1}{3}\right) \approx 0.69 - 0.58 > 0$$
- $$f\left(\frac{1}{2}\right) \approx 0.58 - 0.71 < 0$$，故零点在 $$\left(\frac{1}{3}, \frac{1}{2}\right)$$。选 B。
7. 题目解析：
- A：$$f(x) = \sin 2x$$ 振荡，非单调增。
- B：$$f(x) = xe^x$$ 的导数 $$f'(x) = e^x(x + 1) > 0$$，单调增。
- C：$$f(x) = x^3 - x$$ 在 $$(0, 1)$$ 上导数 $$f'(x) = 3x^2 - 1$$ 可能为负。
- D：$$f(x) = -x + \ln x$$ 的导数 $$f'(x) = -1 + \frac{1}{x}$$ 在 $$x > 1$$ 时为负。
故选 B。
8. 题目解析：
9. 题目解析：
- A：$$y = 3^x$$ 单调增。
- B：$$y = x^2 - 2x + 3$$ 在 $$(1, +\infty)$$ 单调增。
- C：$$y = x$$ 单调增。
- D：$$y = -x^2 - 4x + 3$$ 的导数 $$y' = -2x - 4 < 0$$ 在 $$x > -2$$ 时成立，故在 $$(-1, +\infty)$$ 单调减。
故选 D。
10. 题目解析：
- A：$$y = \sin x$$ 非单调。
- B：$$y = x^3 - x$$ 非单调。
- C：$$y = 2^x$$ 非奇函数。
- D：$$y = \lg(x + \sqrt{x^2 + 1})$$ 是奇函数且单调增。
故选 D。