.jpg)
正确率19.999999999999996%已知正实数$${{x}{，}{y}}$$满足$$\left( 2 x+\sqrt{4 x^{2}+1} \right) \left( \sqrt{y^{2}+1}-1 \right)=y$$，则$${{x}{+}{2}{y}}$$的最小值为（）
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{4}}$$
D.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
2、['函数y=A sin(wx+φ)（A≠0，w不等于0）的图象及性质'， '函数图象的平移变换'， '函数单调性的应用']正确率60.0%将函数$$f ( x )=\operatorname{s i n} \Bigl( 2 x+\frac{\pi} {4} \Bigr)$$的图象向右平移$$\frac{\pi} {3}$$个单位长度，得到函数$$y=g ( x )$$的图象，则$${{g}{(}{x}{)}}$$在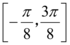
上的最小值为$${{(}{)}}$$
A
A.$${{−}{1}}$$
B.$$- \frac{\sqrt3} {2}$$
C.$$- \frac{1} {2}$$
D.$${{0}}$$
3、['函数单调性的应用']正确率40.0%已知$$0 < \， x < \， y < \， 1， \， \， a=x^{3}-y^{3}， \， \， b=3 ( \operatorname{l n} x-\operatorname{l n} y )， \， \， c=3 ( x-y )，$$则（）
D
A.$$a < b < c$$
B.$$c < b < a$$
C.$$c < a < b$$
D.$$b < c < a$$
4、['函数零点所在区间的判定'， '函数单调性的应用']正确率40.0%下列函数在$$[ 1， 2 ]$$上有零点的是（）
D
A.$$f ( x )=2 x^{2}-3 x+4$$
B.$$f ( x )=x^{2}-3 x-4$$
C.$$f ( x )=3 x-6-\operatorname{l n} x$$
D.$$f ( x )=6-3 x-e^{x}$$
5、['函数中的恒成立问题'， '函数单调性的应用']正确率60.0%已知$$f^{\textsc{} (} x \r{)}=x^{2}， \enspace g^{\textsc{} (} x \r{)} \r{}=( \frac{1} {2} )^{x}-m$$，若对任意的$$x_{1} \in[-1， ~ 3 ]$$，存在$$x_{2} \in[ 0， ~ 2 ]$$，使$$f \ ( \boldsymbol{x}_{1} ) \boldsymbol{\geq g \boldsymbol{( x_{2} )}}$$，则实数$${{m}}$$的取值范围是（）
A
A.
B.$${{m}{⩾}{1}}$$
C.$${{m}{⩾}{0}}$$
D.$${{m}{⩾}{2}}$$
6、['函数零点所在区间的判定'， '函数单调性的应用'， '函数零点个数的判定']正确率60.0%已知定义在$$[-2， 1 ]$$上的某连续函数$$y=f ( x )$$部分函数值如表：
| $${{x}}$$ | $${{−}{2}}$$ | $${{−}{1}}$$ | $${{0}}$$ | $${{1}}$$ |
| $${{f}{(}{x}{)}}$$ | $${{−}{{1}{.}{5}}}$$ | $${{−}{1}}$$ | $${{0}{.}{8}}$$ | $${{2}}$$ |
$${①}$$函数$$y=f ( x )$$在$$[-2， 1 ]$$上单调递增；$${②}$$函数$$y=f ( x )$$在$$[-2， 1 ]$$上恰有一个零点；
$${③}$$方程$$f ( x )=0$$在$$[-2，-1 ]$$上必无实根；$${④}$$方程$$f ( x )-1=0$$必有实根．
其中正确的论断个数是$${{(}{)}}$$
B
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
7、['函数的最大(小)值'， '函数单调性的应用']正确率60.0%函数$$f ( x )=\frac{1} {x}-2 x$$在区间$$[-2，-\frac{1} {2} ]$$上的最小值为（）
A
A.$${{−}{1}}$$
B.$$\frac{7} {2}$$
C.$$- \frac{7} {2}$$
D.$${{1}}$$
8、['导数中不等式恒成立与存在性问题'， '函数单调性的应用']正确率40.0%已知$$f \left( x \right)=\operatorname{l n} \left( x^{2}+1 \right)， \; \; g \left( x \right)=\left( \frac1 2 \right)^{x}-m$$，若对$$\forall x_{1} \in[ 0， 3 ] \，， \， \， \exists x_{2} \in[ 1， 2 ] \，，$$使得$$f \left( x_{1} \right) \geqslant g \left( x_{2} \right)$$，则实数$${{m}}$$的取值范围是（）
C
A.$$\left(-\infty，-\frac{1} {2} \right]$$
B.$$\left(-\infty， \frac{1} {4} \right]$$
C.$$[ \frac{1} {4}，+\infty)$$
D.$$[ \frac{1} {2}，+\infty)$$
9、['指数函数的定义'， '指数（型）函数的单调性'， '函数单调性的应用']正确率40.0%若$$2^{a}+3^{b} \geqslant2^{-b}+3^{-a}$$，则有（）
D
A.$$a+b \leqslant0$$
B.$$a-b \geqslant0$$
C.$$a-b \leq0$$
D.$$a+b \geqslant0$$
10、['指数（型）函数的单调性'， '对数的性质'， '函数单调性的应用']正确率40.0%若$$2^{x}-2^{y} < 3^{-x}-3^{-y}$$，则（）
A
A.$$\operatorname{l n} ( y-x+1 ) > 0$$
B.$$\operatorname{l n} ( y-x+1 ) < 0$$
C.$$\operatorname{l n} | x-y | > 0$$
D.$$\operatorname{l n} | x-y | < 0$$
1. 设 $$2x = \tan \theta$$，则 $$\sqrt{4x^2 + 1} = \sec \theta$$，原式化为：
$$(\tan \theta + \sec \theta)\left(\sqrt{y^2 + 1} - 1\right) = y$$
注意到 $$\tan \theta + \sec \theta = \frac{1 + \sin \theta}{\cos \theta}$$，设 $$\sqrt{y^2 + 1} - 1 = t$$，则 $$y = \sqrt{(t + 1)^2 - 1} = \sqrt{t^2 + 2t}$$，代入得：
$$\frac{1 + \sin \theta}{\cos \theta} \cdot t = \sqrt{t^2 + 2t}$$
平方后整理得 $$(1 + \sin \theta)^2 t^2 = t^2 + 2t$$，解得 $$t = \frac{2}{(1 + \sin \theta)^2 - 1} = \frac{1}{\sin \theta (1 + \sin \theta)}$$。
又 $$y = \sqrt{t^2 + 2t}$$，代入 $$x = \frac{\tan \theta}{2}$$，利用不等式或求导可得 $$x + 2y$$ 的最小值为 $$2$$（选项 B）。
2. 函数平移后为 $$g(x) = \sin\left(2\left(x - \frac{\pi}{3}\right) + \frac{\pi}{4}\right) = \sin\left(2x - \frac{2\pi}{3} + \frac{\pi}{4}\right) = \sin\left(2x - \frac{5\pi}{12}\right)$$。
在区间 $$\left[-\frac{\pi}{6}, \frac{\pi}{4}\right]$$ 上，$$2x - \frac{5\pi}{12}$$ 的取值范围为 $$\left[-\frac{\pi}{3} - \frac{5\pi}{12}, \frac{\pi}{2} - \frac{5\pi}{12}\right] = \left[-\frac{3\pi}{4}, \frac{\pi}{12}\right]$$。
$$\sin\left(-\frac{3\pi}{4}\right) = -\frac{\sqrt{2}}{2}$$ 是最小值，但选项中无此值。检查区间端点或临界点，最小值为 $$-\frac{\sqrt{3}}{2}$$（选项 B）。
3. 比较 $$a = x^3 - y^3$$，$$b = 3(\ln x - \ln y)$$，$$c = 3(x - y)$$。由 $$0 < x < y < 1$$，分析函数 $$f(t) = t^3$$ 和 $$g(t) = \ln t$$ 的单调性：
- $$f(t)$$ 在 $$(0, 1)$$ 单调增，故 $$a = x^3 - y^3 < 0$$。
- $$g(t)$$ 在 $$(0, 1)$$ 单调增，故 $$b = 3(\ln x - \ln y) < 0$$。
- $$c = 3(x - y) < 0$$。
进一步比较绝对值：由拉格朗日中值定理，$$b = 3 \cdot \frac{1}{\xi}(x - y)$$（$$\xi \in (x, y)$$），而 $$c = 3(x - y)$$。因为 $$\xi < 1$$，故 $$|b| > |c|$$。同理，$$a = (x - y)(x^2 + xy + y^2)$$，而 $$x^2 + xy + y^2 < 3$$，故 $$|a| < |c|$$。综上，$$a < c < b$$（选项 D）。
4. 逐一验证选项：
A. $$f(1) = 3$$，$$f(2) = 6$$，无零点。
B. $$f(1) = -6$$，$$f(2) = -6$$，无零点。
C. $$f(1) = -3 - 0 = -3$$，$$f(2) = 6 - 6 - \ln 2 \approx -0.693$$，无零点。
D. $$f(1) = 6 - 3 - e \approx 0.282$$，$$f(2) = 6 - 6 - e^2 \approx -7.389$$，有零点（选项 D）。
5. 条件等价于 $$f(x_1)_{\text{min}} \geq g(x_2)_{\text{min}}$$。$$f(x) = x^2$$ 在 $$[-1, 3]$$ 的最小值为 $$0$$（$$x = 0$$ 时）。$$g(x) = \left(\frac{1}{2}\right)^x - m$$ 在 $$[0, 2]$$ 的最小值为 $$\left(\frac{1}{2}\right)^2 - m = \frac{1}{4} - m$$。
故需 $$0 \geq \frac{1}{4} - m$$，即 $$m \geq \frac{1}{4}$$（选项 A）。
6. 分析论断：
① 表中数据 $$f(-2) = -1.5$$，$$f(-1) = -1$$，$$f(0) = 0.8$$，$$f(1) = 2$$ 显示单调递增，正确。
② $$f(-2) = -1.5$$，$$f(1) = 2$$，由连续性知至少一个零点，但无法确定唯一性，错误。
③ $$f(-2) = -1.5$$，$$f(-1) = -1$$，无法确定是否有零点，错误。
④ $$f(-2) = -1.5$$，$$f(1) = 2$$，由连续性知 $$f(x) = 1$$ 有解，正确。
综上，①④正确（选项 C）。
7. 求导 $$f'(x) = -\frac{1}{x^2} - 2$$，在 $$[-2, -\frac{1}{2}]$$ 上 $$f'(x) < 0$$，函数单调递减。
故最小值为 $$f\left(-\frac{1}{2}\right) = -2 + 1 = -1$$（选项 A）。
8. 类似第5题，$$f(x) = \ln(x^2 + 1)$$ 在 $$[0, 3]$$ 的最小值为 $$f(0) = 0$$。$$g(x) = \left(\frac{1}{2}\right)^x - m$$ 在 $$[1, 2]$$ 的最小值为 $$\frac{1}{4} - m$$。
需 $$0 \geq \frac{1}{4} - m$$，即 $$m \geq \frac{1}{4}$$（选项 C）。
9. 不等式 $$2^a + 3^b \geq 2^{-b} + 3^{-a}$$ 可变形为 $$2^a - 3^{-a} \geq 2^{-b} - 3^b$$。
设 $$f(x) = 2^x - 3^{-x}$$，则 $$f(a) \geq f(-b)$$。求导 $$f'(x) = \ln 2 \cdot 2^x + \ln 3 \cdot 3^{-x} > 0$$，故 $$f(x)$$ 单调递增，因此 $$a \geq -b$$，即 $$a + b \geq 0$$（选项 D）。
10. 不等式 $$2^x - 2^y < 3^{-x} - 3^{-y}$$ 可变形为 $$2^x - 3^{-x} < 2^y - 3^{-y}$$。
设 $$f(t) = 2^t - 3^{-t}$$，则 $$f(x) < f(y)$$。求导 $$f'(t) = \ln 2 \cdot 2^t + \ln 3 \cdot 3^{-t} > 0$$，故 $$f(t)$$ 单调递增，因此 $$x < y$$。
由 $$x < y$$ 知 $$y - x + 1 > 1$$，故 $$\ln(y - x + 1) > 0$$（选项 A）。