正确率60.0%已知函数$$y=f ( x ), \, \, \, x \in{\bf R},$$则“$$y=| f ( x ) |$$是偶函数”是“$$y=f ( x )$$的图象关于原点对称”的()
B
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
2、['函数奇、偶性的图象特征', '函数奇、偶性的定义']正确率60.0%函数$$f ( x )=x^{2}-1$$的图象关于()
B
A.$${{x}}$$轴对称
B.$${{y}}$$轴对称
C.坐标原点对称
D.直线$${{y}{=}{x}}$$轴对称
3、['函数奇、偶性的图象特征', '函数图象的识别', '函数单调性的应用']正确率60.0%函数$$f ( x )=1+\frac{2 \mathrm{e}^{-x}} {\mathrm{e}^{x}-\mathrm{e}^{-x}}$$的图象大致是()
C
A.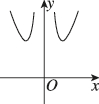
B.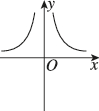
C.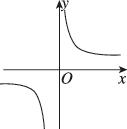
D.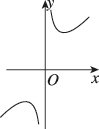
正确率60.0%函数$$f ( x )=\frac{x} {\sqrt{1+x^{2}}}$$的图象大致是()
C
A.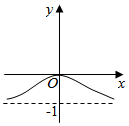
B.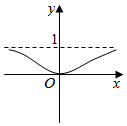
C.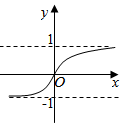
D.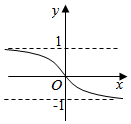
正确率40.0%已知函数$$g ( x )=\operatorname{c o s} \Bigl( \frac{\pi} {3}+x \Bigr)+\operatorname{s i n} \Bigl( \frac{\pi} {6}+x \Bigr)$$,设函数$$f ( x )=\frac{1} {4} x^{2}+g ( x )$$,函数$${{f}{(}{x}{)}}$$的导函数为$$f^{\prime} ( x )$$,则函数$$f^{\prime} ( x )$$的图象大致为$${{(}{)}}$$
A
A.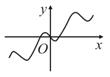
B.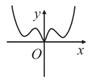
C.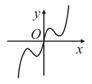
D.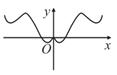
正确率60.0%函数$$f ( x )=x \operatorname{c o s} x-\operatorname{s i n} x, \, \, \, x \in[-\pi, \pi]$$的大致图像为()
D
A.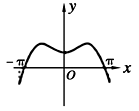
B.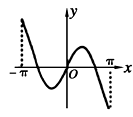
C.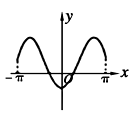
D.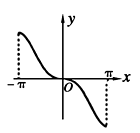
正确率40.0%函数$$f ( x )=x \mathrm{c o s} x-\mathrm{s i n} x$$在$$x \in[-3 \pi, 3 \pi]$$的大致图象为$${{(}{)}}$$
A
A.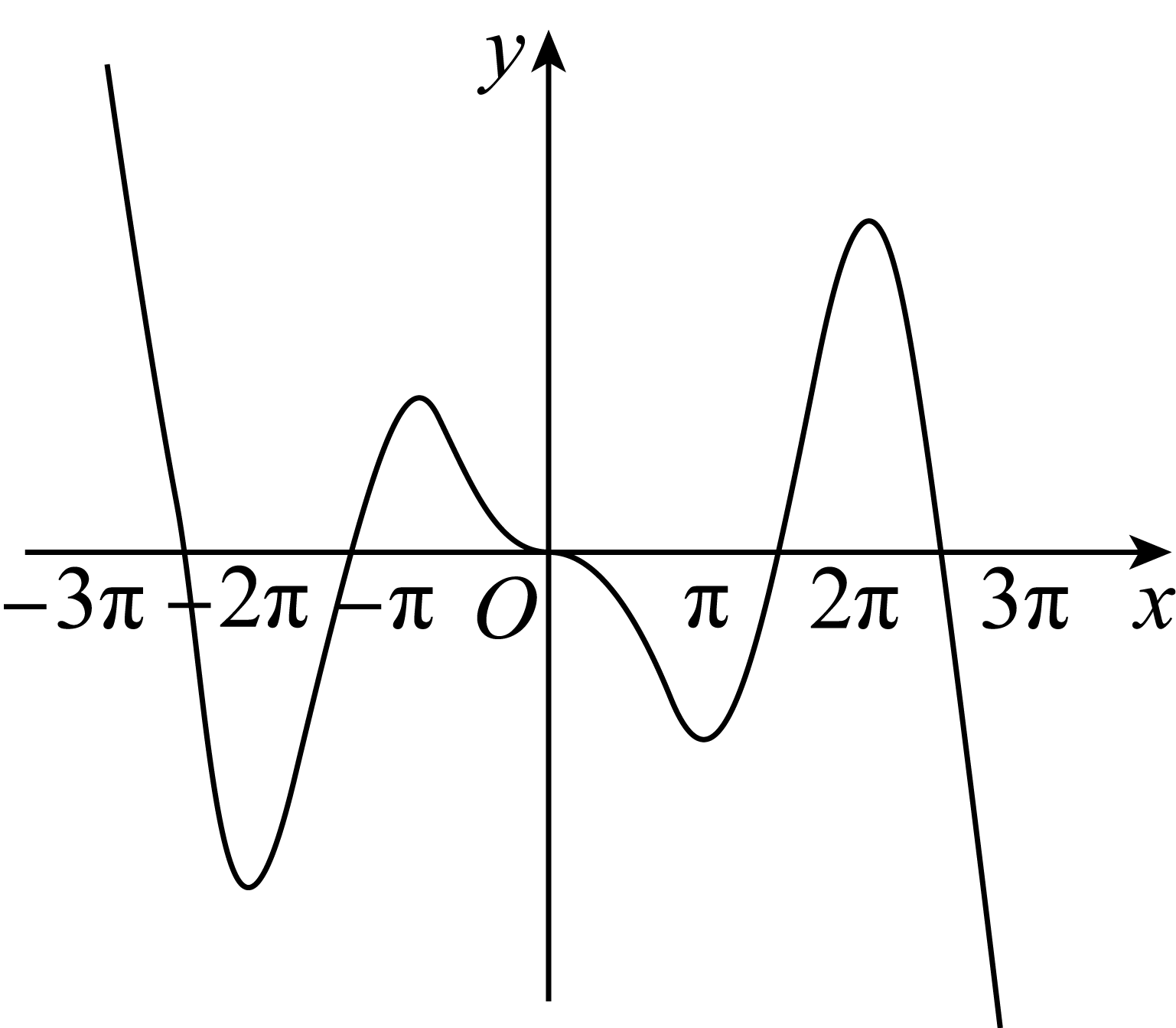
B.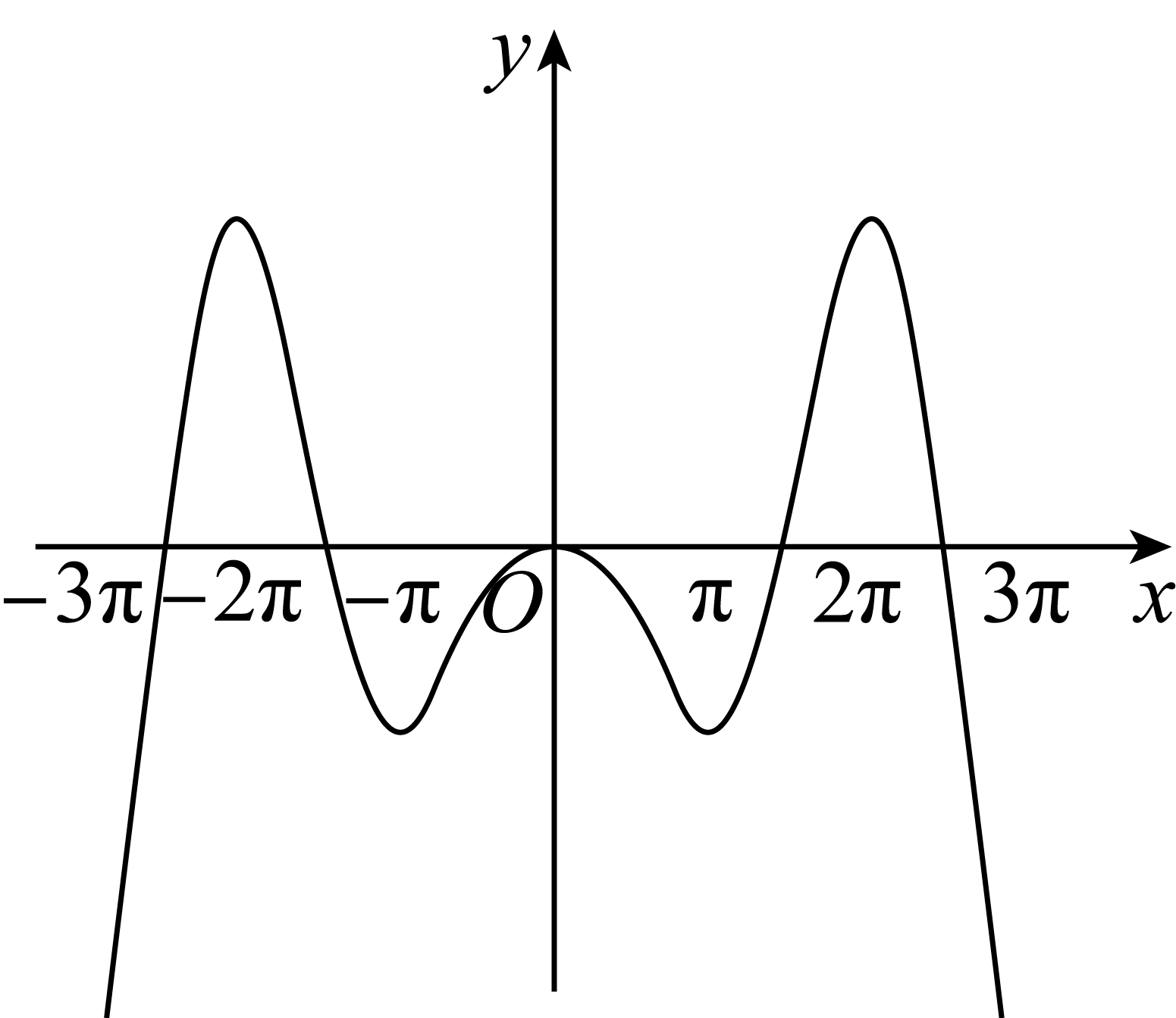
C.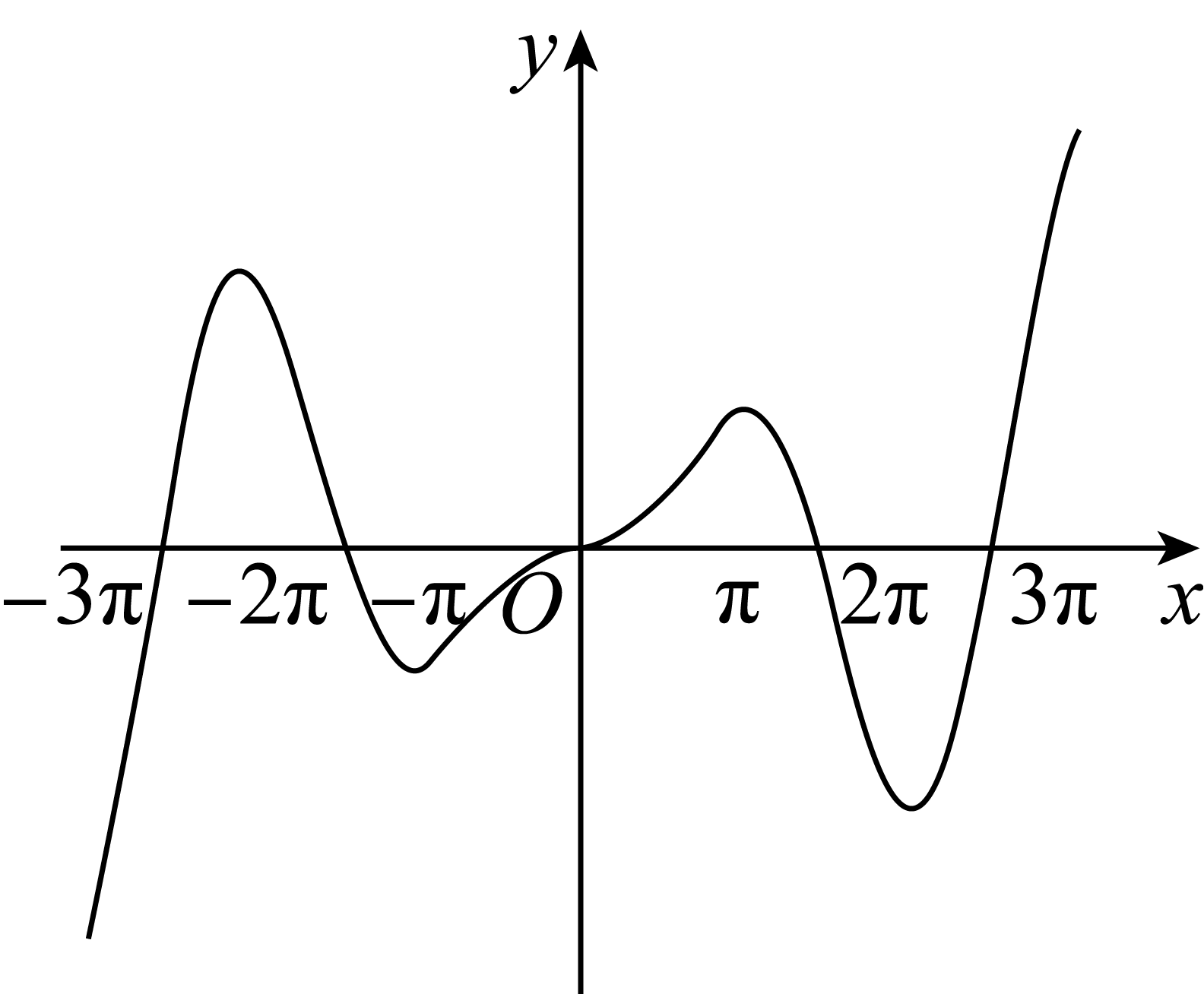
D.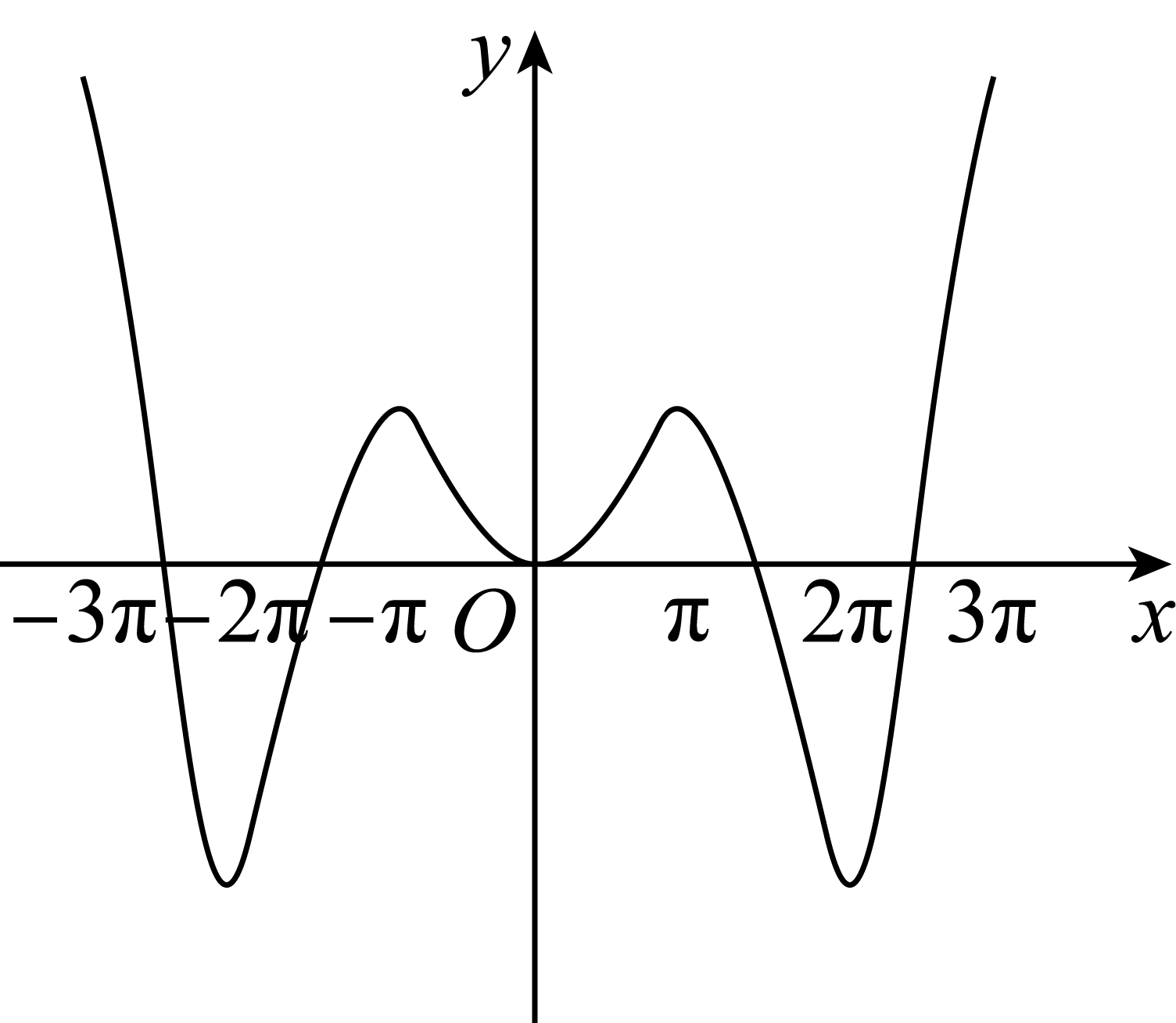
正确率40.0%已知$${{f}{{(}{x}{)}}}$$是定义是$${{R}}$$上的奇函数,满足$$f \left(-\frac{3} {2}+x \right)=f \left( \frac{3} {2}+x \right)$$,当$$x \in\left( 0, \frac{3} {2} \right)$$时,$$f \left( x \right)=\operatorname{l n} \left( x^{2} \!-\! x \!+\! 1 \right)$$,则函数$${{f}{{(}{x}{)}}}$$在区间$$( 0, 6 )$$上的零点个数是()
C
A.$${{3}}$$
B.$${{5}}$$
C.$${{7}}$$
D.$${{9}}$$
9、['函数奇、偶性的图象特征', '函数图象的识别', '函数求值']正确率60.0%函数$$y=x^{3}+\operatorname{l n} \! \left( \sqrt{x^{2}+1}-x \right)$$的图象大致为()
C
A.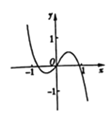
B.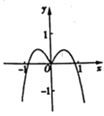
C.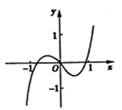
D.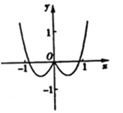
正确率60.0%函数$$f ( x )=\frac{\operatorname{c o s} 2 x} {| x |}$$的图象可能是()
C
A.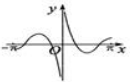
B.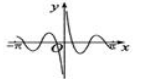
C.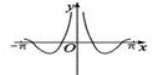
D.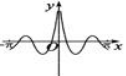
1. 题目解析:
首先分析条件“$$y=|f(x)|$$是偶函数”意味着$$|f(-x)|=|f(x)|$$对所有$$x$$成立。这并不一定要求$$f(x)$$本身是奇函数(关于原点对称),例如$$f(x)=x^2$$满足$$|f(-x)|=|f(x)|$$,但其图象关于$$y$$轴对称而非原点对称。反过来,如果$$y=f(x)$$的图象关于原点对称(即$$f(x)$$是奇函数),则$$f(-x)=-f(x)$$,从而$$|f(-x)|=|-f(x)|=|f(x)|$$,即$$y=|f(x)|$$是偶函数。因此,“$$y=|f(x)|$$是偶函数”是“$$y=f(x)$$的图象关于原点对称”的必要不充分条件,答案为$$B$$。
2. 题目解析:
函数$$f(x)=x^2-1$$是一个二次函数,其图象为抛物线。由于$$f(-x)=(-x)^2-1=x^2-1=f(x)$$,函数为偶函数,图象关于$$y$$轴对称。因此答案为$$B$$。
3. 题目解析:
函数$$f(x)=1+\frac{2e^{-x}}{e^x-e^{-x}}$$可以化简为$$f(x)=1+\frac{2}{e^{2x}-1}$$。当$$x\to+\infty$$时,$$e^{2x}\to+\infty$$,$$f(x)\to1$$;当$$x\to0^+$$时,$$e^{2x}-1\to0^+$$,$$f(x)\to+\infty$$;当$$x\to0^-$$时,$$e^{2x}-1\to0^-$$,$$f(x)\to-\infty$$。因此图象在$$x=0$$处有垂直渐近线,且左右两侧趋向于不同方向的无穷大,符合选项$$A$$的特征。
4. 题目解析:
函数$$f(x)=\frac{x}{\sqrt{1+x^2}}$$的定义域为全体实数。计算$$f(-x)=\frac{-x}{\sqrt{1+x^2}}=-f(x)$$,说明函数为奇函数,图象关于原点对称。当$$x\to+\infty$$时,$$f(x)\to1$$;当$$x\to-\infty$$时,$$f(x)\to-1$$。因此图象在$$y=\pm1$$处有水平渐近线,且通过原点,符合选项$$A$$的特征。
5. 题目解析:
首先化简$$g(x)=\cos\left(\frac{\pi}{3}+x\right)+\sin\left(\frac{\pi}{6}+x\right)$$。利用三角恒等式,$$\cos\left(\frac{\pi}{3}+x\right)=\cos\frac{\pi}{3}\cos x-\sin\frac{\pi}{3}\sin x$$,$$\sin\left(\frac{\pi}{6}+x\right)=\sin\frac{\pi}{6}\cos x+\cos\frac{\pi}{6}\sin x$$。代入得$$g(x)=\cos x$$。因此$$f(x)=\frac{1}{4}x^2+\cos x$$,导数为$$f'(x)=\frac{1}{2}x-\sin x$$。观察$$f'(x)$$的图象,当$$x=0$$时$$f'(0)=0$$,且$$f'(x)$$为奇函数,图象关于原点对称,符合选项$$D$$的特征。
6. 题目解析:
函数$$f(x)=x\cos x-\sin x$$在区间$$[-\pi,\pi]$$上分析:
- $$f(-x)=-x\cos(-x)-\sin(-x)=-x\cos x+\sin x=-(x\cos x-\sin x)=-f(x)$$,说明函数为奇函数,图象关于原点对称。
- $$f(0)=0$$,$$f(\pi)=-\pi-0=-\pi$$,$$f(-\pi)=\pi-0=\pi$$。
- 导数$$f'(x)=\cos x-x\sin x-\cos x=-x\sin x$$,在$$(0,\pi)$$上$$f'(x)\leq0$$,函数单调递减;在$$(-\pi,0)$$上$$f'(x)\geq0$$,函数单调递增。
因此图象在$$x=0$$处有极大值,符合选项$$A$$的特征。
7. 题目解析:
函数$$f(x)=x\cos x-\sin x$$在区间$$[-3\pi,3\pi]$$上分析:
- 函数为奇函数,图象关于原点对称。
- $$f(0)=0$$,$$f(\pi)=-\pi$$,$$f(2\pi)=2\pi$$,$$f(3\pi)=-3\pi$$。
- 导数$$f'(x)=-x\sin x$$,函数在$$(2k\pi,(2k+1)\pi)$$上单调递减,在$$((2k-1)\pi,2k\pi)$$上单调递增($$k\in\mathbb{Z}$$)。
因此图象在$$x=0$$处有极大值,整体呈现振荡衰减趋势,符合选项$$A$$的特征。
8. 题目解析:
函数$$f(x)$$是奇函数,且满足$$f\left(-\frac{3}{2}+x\right)=f\left(\frac{3}{2}+x\right)$$,说明函数关于$$x=0$$对称且具有周期性。在$$(0,\frac{3}{2})$$上$$f(x)=\ln(x^2-x+1)$$,零点为$$x=1$$。由于$$f(x)$$在$$(0,6)$$上有周期性,每个周期长度为3,因此在$$(0,6)$$上有$$x=1,2,4,5$$四个零点,加上$$x=0$$和$$x=3$$(因为$$f(0)=0$$且$$f(3)=f(0)=0$$),总共有5个零点,答案为$$B$$。
9. 题目解析:
函数$$y=x^3+\ln(\sqrt{x^2+1}-x)$$分析:
- 定义域为全体实数,因为$$\sqrt{x^2+1}>|x|\geq x$$。
- $$y(-x)=-x^3+\ln(\sqrt{x^2+1}+x)=-x^3+\ln\left(\frac{1}{\sqrt{x^2+1}-x}\right)=-x^3-\ln(\sqrt{x^2+1}-x)=-y(x)$$,说明函数为奇函数,图象关于原点对称。
- 当$$x\to+\infty$$时,$$\ln(\sqrt{x^2+1}-x)\to-\infty$$,但$$x^3$$主导,$$y\to+\infty$$;当$$x\to-\infty$$时,$$y\to-\infty$$。
因此图象符合选项$$A$$的特征。
10. 题目解析:
函数$$f(x)=\frac{\cos2x}{|x|}$$分析:
- 定义域为$$x\neq0$$。
- $$f(-x)=\frac{\cos(-2x)}{|-x|}=\frac{\cos2x}{|x|}=f(x)$$,说明函数为偶函数,图象关于$$y$$轴对称。
- 当$$x\to0$$时,$$f(x)\to+\infty$$,有垂直渐近线$$x=0$$。
- 当$$x\to\pm\infty$$时,$$f(x)\to0$$,有水平渐近线$$y=0$$。
因此图象符合选项$$A$$的特征。
.jpg)