正确率60.0%已知函数$$f ( x )=\frac{x} {1+x},$$则()
B
A.$${{f}{(}{x}{)}}$$在$$(-\infty, ~-1 ) \cup(-1, ~+\infty)$$上单调递增
B.$${{f}{(}{x}{)}}$$在$$(-\infty, ~-1 )$$和$$(-1, ~+\infty)$$上单调递增
C.$${{f}{(}{x}{)}}$$在$$(-\infty, ~-1 )$$和$$(-1, ~+\infty)$$上单调递减
D.$${{f}{(}{x}{)}}$$在$$(-\infty, ~-1 )$$上单调递增,在$$(-1, ~+\infty)$$上单调递减
2、['平均变化率与函数的单调性']正确率80.0%已知函数$$f ( x )=x^{2}+2,$$则该函数在区间$$[ 1, ~ 3 ]$$上的平均变化率为()
A
A.$${{4}}$$
B.$${{3}}$$
C.$${{2}}$$
D.$${{1}}$$
3、['平均变化率与函数的单调性']正确率60.0%已知函数$$f ( x )=a x^{2}$$在区间$$[ 1, \ 2 ]$$上的平均变化率为$${\sqrt {3}{,}}$$则$${{f}{(}{x}{)}}$$在区间$$[-2, ~-1 ]$$上的平均变化率为()
A
A.$${{−}{\sqrt {3}}}$$
B.$${\sqrt {3}}$$
C.$$- \frac{\sqrt3} {3}$$
D.$$\frac{\sqrt{3}} {3}$$
4、['平均变化率与函数的单调性']正确率60.0%如图所示,单位圆中弧$${{A}{B}}$$的长为$$x, ~ f ( x )$$表示弧$${{A}{B}}$$与弦$${{A}{B}}$$所围成的弓形面积的$${{2}}$$倍,则函数$$y=f ( x )$$的大致图象是()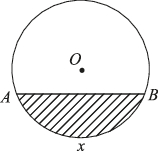
D
A.
B.
C.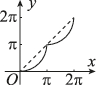
D.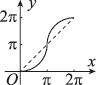
正确率60.0%汽车行驶的路程$${{s}}$$和时间$${{t}}$$之间的函数图象如图,设汽车在时间段$$[ t_{0}, ~ t_{1} ], ~ [ t_{1}, ~ t_{2} ], ~ [ t_{2}, ~ t_{3} ]$$内的平均速度分别为$$v_{1}, ~ v_{2}, ~ v_{3},$$则()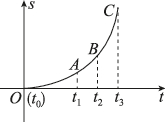
A
A.$$v_{1} < v_{2} < v_{3}$$
B.$$v_{1} < v_{3} < v_{2}$$
C.$$v_{3} < v_{2} < v_{1}$$
D.$$v_{2} < v_{3} < v_{1}$$
6、['平均变化率与函数的单调性', '两点间的斜率公式']正确率80.0%若经过$$A ( 4, ~ 2 y+1 ), ~ B ( 2, ~-3 )$$两点的直线的斜率为$${{−}{1}{,}}$$则$${{y}{=}}$$()
B
A.$${{−}{1}}$$
B.$${{−}{3}}$$
C.$${{0}}$$
D.$${{2}}$$
7、['平均变化率与函数的单调性', '两点间的斜率公式', '直线的斜率']正确率60.0%已知函数$$f ( x ) ( 0 \leqslant x \leqslant1 )$$的图象的一段圆弧(如图所示)若$$0 < x_{1} < x_{2} < 1$$,则$${{(}{)}}$$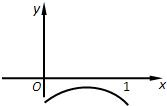
D
A.$$\frac{f ( x_{1} )} {x_{1}} < \frac{f ( x_{2} )} {x_{2}}$$
B.$$\frac{f ( x_{1} )} {x_{1}}=\frac{f ( x_{2} )} {x_{2}}$$
C.$$\frac{f ( x_{1} )} {x_{1}} > \frac{f ( x_{2} )} {x_{2}}$$
D.前三个判断都不正确
8、['平均变化率与函数的单调性']正确率60.0%已知函数$$f ( x )=2 x^{2}-4$$的图象上一点$$( 1,-2 )$$及邻近一点$$( 1+\Delta x,-2+\Delta y ),$$则$$\frac{\Delta y} {\Delta x}$$等于()
C
A.$${{4}}$$
B.$${{4}{x}}$$
C.$$4+2 \Delta x$$
D.$$4+2 ( \Delta x )^{2}$$
9、['平均变化率与函数的单调性']正确率80.0%若函数$$y=a x+b$$在区间$$[ 1, 2 ]$$上的平均变化率为$${{3}}$$,则$${{a}{=}}$$()
C
A.$${{−}{3}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{−}{2}}$$
10、['平均变化率与函数的单调性', '单调性的定义与证明', '函数单调性的判断']正确率60.0%定义在$${{R}}$$上的函数$${{f}{(}{x}{)}}$$对任意两个不相等的实数$${{a}{,}{b}{,}}$$总有$$\frac{f ( a )-f ( b )} {a-b} > 0$$成立,则必有 ()
A
A.$${{f}{(}{x}{)}}$$在$${{R}}$$上是增函数
B.$${{f}{(}{x}{)}}$$在$${{R}}$$上是减函数
C.函数$${{f}{(}{x}{)}}$$在$${{R}}$$上先增加后减少
D.函数$${{f}{(}{x}{)}}$$在$${{R}}$$上先减少后增加
1. 解析:函数 $$f(x) = \frac{x}{1+x}$$ 的导数为 $$f'(x) = \frac{1}{(1+x)^2}$$。由于分母 $$(1+x)^2$$ 恒为正($$x \neq -1$$),故 $$f'(x) > 0$$ 在定义域 $$(-\infty, -1) \cup (-1, +\infty)$$ 上成立,因此函数在两个区间内均单调递增。选项 B 正确。
2. 解析:平均变化率为 $$\frac{f(3) - f(1)}{3 - 1} = \frac{(9 + 2) - (1 + 2)}{2} = \frac{8}{2} = 4$$。选项 A 正确。
3. 解析:由题意,$$\frac{f(2) - f(1)}{2 - 1} = 4a - a = 3a = \sqrt{3}$$,解得 $$a = \frac{\sqrt{3}}{3}$$。在区间 $$[-2, -1]$$ 上,平均变化率为 $$\frac{f(-1) - f(-2)}{-1 - (-2)} = \frac{a - 4a}{1} = -3a = -\sqrt{3}$$。选项 A 正确。
4. 解析:弓形面积为扇形面积减去三角形面积,即 $$f(x) = 2\left(\frac{x}{2} - \frac{\sin x}{2}\right) = x - \sin x$$。其图像在 $$[0, \pi]$$ 上单调递增且下凸,选项 C 符合。
5. 解析:平均速度为路程与时间的比值。从图像看,$$[t_0, t_1]$$ 斜率最小,$$[t_2, t_3]$$ 斜率最大,故 $$v_1 < v_2 < v_3$$。选项 A 正确。
6. 解析:斜率公式为 $$\frac{2y + 1 - (-3)}{4 - 2} = \frac{2y + 4}{2} = y + 2 = -1$$,解得 $$y = -3$$。选项 B 正确。
7. 解析:圆弧图像为下凸函数,故 $$\frac{f(x)}{x}$$ 随 $$x$$ 增大而减小,因此 $$\frac{f(x_1)}{x_1} > \frac{f(x_2)}{x_2}$$。选项 C 正确。
8. 解析:$$\Delta y = f(1 + \Delta x) - f(1) = 2(1 + \Delta x)^2 - 4 - (-2) = 2 + 4\Delta x + 2(\Delta x)^2$$,故 $$\frac{\Delta y}{\Delta x} = 4 + 2\Delta x$$。选项 C 正确。
9. 解析:平均变化率为 $$\frac{f(2) - f(1)}{2 - 1} = (2a + b) - (a + b) = a = 3$$。选项 C 正确。
10. 解析:条件 $$\frac{f(a) - f(b)}{a - b} > 0$$ 表明函数在任意两点间斜率均为正,故 $$f(x)$$ 在 $$R$$ 上单调递增。选项 A 正确。
.jpg)