正确率60.0%下列函数是奇函数的是()
A
A.$$f \mid\alpha) ~=\l g$$$$( 1+x ) ~-l g$$$$( 1-x )$$
B.$$f \left( \textbf{x} \right) ~=2^{x}+2^{-x}$$
C.$$f ~ ( \boldsymbol{x} ) ~=-| \boldsymbol{x} |$$
D.$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=x^{3}-1$$
2、['函数奇偶性的应用', '指数(型)函数的单调性', '函数奇、偶性的图象特征']正确率60.0%设奇函数$${{f}{(}{x}{)}}$$的定义域为$$[-5, 5 ]$$,且$$f ( 3 )=0$$,当$$x \in[ 0, 5 ]$$时,$${{f}{(}{x}{)}}$$的图象如图所示,则不等式$$e^{f ( x )} < 1$$的解集是$${{(}{)}}$$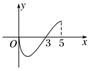
C
A.$$(-3, 0 ) \cup( 3, 5 ]$$
B.$$(-3, 0 ) \cup( 0, 3 )$$
C.$$[-5,-3 ) \cup( 0, 3 )$$
D.$$( 0, 3 )$$
3、['函数奇、偶性的图象特征', '函数图象的识别', '函数单调性的应用']正确率40.0%函数$$f ( x )=\frac{2} {\pi} x-\operatorname{s i n} x ( x \in R )$$的部分图象是
D
A.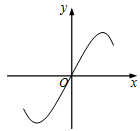
B.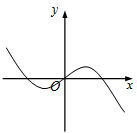
C.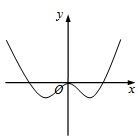
D.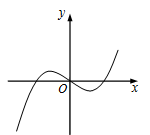
正确率40.0%已知函数$$y=f ( x )$$的图像如图所示,则$${{f}{(}{x}{)}}$$的解析式可能是$${{(}{)}}$$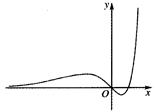
A
A.$$y=( \frac{1} {2} x^{2}-x ) e^{x}$$
B.$$\frac{e^{x} \operatorname{s i n} x} {e^{2 x}+1}$$
C.$$y=\frac{\operatorname{l n} x} {x}$$
D.$$y=x^{3}-3 x$$
5、['函数奇、偶性的证明', '函数奇、偶性的图象特征']正确率60.0%$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=\frac{4^{x}+1} {2^{x}}$$的图象下列叙述正确的是()
C
A.关于原点对称
B.关于$${{x}}$$轴对称
C.关于$${{y}}$$轴对称
D.没有对称性
6、['函数奇偶性的应用', '函数的最大(小)值', '函数奇、偶性的图象特征', '函数单调性的判断', '利用函数奇偶性求解析式']正确率60.0%已知$${{f}{{(}{x}{)}}}$$是定义在$${{R}}$$上的奇函数,给出下列四个结论:
$$\odot f \left( 0 \right)=0$$;
$${②}$$若函数$${{f}{{(}{x}{)}}}$$在$$[ 0,+\infty)$$上有最小值$${{−}{1}}$$,则$${{f}{{(}{x}{)}}}$$在$$(-\infty, 0 ]$$上有最大值$${{1}}$$;
$${③}$$若函数$${{f}{{(}{x}{)}}}$$在$$[ 1,+\infty)$$上有为增函数,则$${{f}{{(}{x}{)}}}$$在$$(-\infty,-1 ]$$上为减函数;
$${④}$$若$${{x}{>}{0}}$$时,$$f \left( x \right)=x^{2}-2 x$$,则$${{x}{<}{0}}$$时,$$f \left( x \right)=-x^{2}-2 x$$.
其中正确结论的个数为()
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
7、['函数奇、偶性的图象特征', '导数与单调性']正确率60.0%函数$$f \left( x \right)=\frac{x^{2}-1} {\left\vert x \right\vert}$$的图象大致为()
D
A.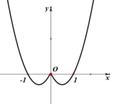
B.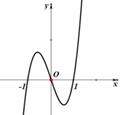
C.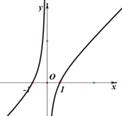
D.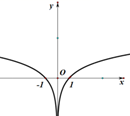
正确率60.0%设函数$$f ( x )=x \mathrm{l n} \frac{1+x} {1-x}$$,则函数$${{f}{(}{x}{)}}$$的图象可能为 ()
B
A.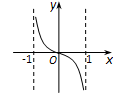
B.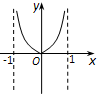
C.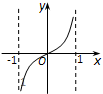
D.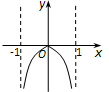
正确率60.0%著名数学家华罗庚先生曾说:$${{“}}$$数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休$${{”}}$$如函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=\frac{\mathrm{e}^{x}-\mathrm{e}^{-x}} {x^{2}}$$的图象大致是()
B
A.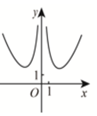
B.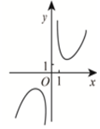
C.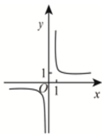
D.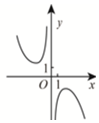
正确率40.0%函数$$f ( x )=x \operatorname{s i n} x+\frac{1} {x^{2}}-\frac{1} {\pi^{2}}$$在区间$$[-2 \pi, 2 \pi]$$上的大致图像为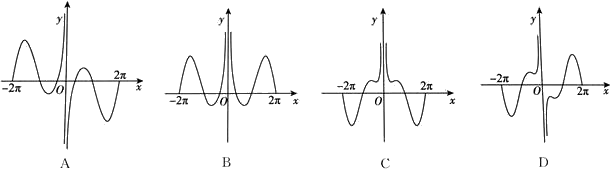
C
A.$${{A}}$$
B.$${{B}}$$
C.$${{C}}$$
D.$${{D}}$$
1. 解析:
奇函数的定义是满足 $$f(-x) = -f(x)$$。
A选项: $$f(x) = \lg(1+x) - \lg(1-x)$$
计算 $$f(-x) = \lg(1-x) - \lg(1+x) = -f(x)$$,因此是奇函数。
B选项: $$f(x) = 2^x + 2^{-x}$$
计算 $$f(-x) = 2^{-x} + 2^x = f(x)$$,是偶函数。
C选项: $$f(x) = -|x|$$
计算 $$f(-x) = -|x| = f(x)$$,是偶函数。
D选项: $$f(x) = x^3 - 1$$
计算 $$f(-x) = -x^3 - 1 \neq -f(x)$$,既不是奇函数也不是偶函数。
正确答案:A
2. 解析:
不等式 $$e^{f(x)} < 1$$ 等价于 $$f(x) < 0$$。
由奇函数性质,$$f(-3) = -f(3) = 0$$。
根据图像,$$f(x) < 0$$ 在 $$[0,5]$$ 上的解集是 $$(0,3)$$。
由奇函数对称性,$$f(x) < 0$$ 在 $$[-5,0]$$ 上的解集是 $$(-3,0)$$。
正确答案:B
3. 解析:
函数 $$f(x) = \frac{2}{\pi}x - \sin x$$。
计算 $$f(0) = 0$$,$$f(\pi/2) = 1 - 1 = 0$$,$$f(-\pi/2) = -1 - (-1) = 0$$。
函数在 $$x > 0$$ 时先增后减,在 $$x < 0$$ 时先减后增,且关于原点对称(奇函数)。
正确答案:B
4. 解析:
观察图像,函数在 $$x=0$$ 处有定义,且为奇函数。
A选项: $$y = \left(\frac{1}{2}x^2 - x\right)e^x$$ 不是奇函数。
B选项: $$y = \frac{e^x \sin x}{e^{2x} + 1}$$ 是奇函数,且符合图像特征。
C选项: $$y = \frac{\ln x}{x}$$ 定义域为 $$x > 0$$,不符合。
D选项: $$y = x^3 - 3x$$ 是奇函数,但图像与给定不符。
正确答案:B
5. 解析:
函数 $$f(x) = \frac{4^x + 1}{2^x} = 2^x + 2^{-x}$$。
计算 $$f(-x) = 2^{-x} + 2^x = f(x)$$,因此是偶函数,关于 $$y$$ 轴对称。
正确答案:C
6. 解析:
①: 奇函数满足 $$f(0) = 0$$,正确。
②: 奇函数在对称区间上的最值相反,正确。
③: 奇函数在对称区间上的单调性相同,错误。
④: 当 $$x < 0$$ 时,$$f(x) = -f(-x) = -((-x)^2 - 2(-x)) = -x^2 - 2x$$,正确。
正确答案:C(①、②、④正确)
7. 解析:
函数 $$f(x) = \frac{x^2 - 1}{|x|}$$ 是偶函数,图像关于 $$y$$ 轴对称。
当 $$x > 0$$ 时,$$f(x) = \frac{x^2 - 1}{x} = x - \frac{1}{x}$$,在 $$x=1$$ 时为 $$0$$,在 $$x \to 0^+$$ 时趋向于 $$-\infty$$。
正确答案:B
8. 解析:
函数 $$f(x) = x \ln \frac{1+x}{1-x}$$ 定义域为 $$-1 < x < 1$$。
计算 $$f(-x) = -x \ln \frac{1-x}{1+x} = x \ln \frac{1+x}{1-x} = f(x)$$,是偶函数。
当 $$x \to 1^-$$ 时,$$f(x) \to +\infty$$;当 $$x \to -1^+$$ 时,$$f(x) \to +\infty$$。
正确答案:D
9. 解析:
函数 $$f(x) = \frac{e^x - e^{-x}}{x^2}$$ 是奇函数。
当 $$x \to 0$$ 时,$$f(x) \approx \frac{2x}{x^2} = \frac{2}{x}$$,趋向于 $$\pm \infty$$。
当 $$x \to +\infty$$ 时,$$f(x) \approx \frac{e^x}{x^2} \to +\infty$$。
正确答案:B
10. 解析:
函数 $$f(x) = x \sin x + \frac{1}{x^2} - \frac{1}{\pi^2}$$。
观察图像,函数在 $$x = \pm \pi$$ 处有极小值,且关于 $$y$$ 轴对称(偶函数)。
正确答案:A
.jpg)