正确率60.0%某物体沿直线运动,其位移$${{s}}$$(单位:$${{m}{)}}$$与时间$${{t}}$$(单位:$${{s}{)}}$$之间的关系为$$s ( t )=\frac{1} {4} t^{2}+t,$$则该物体在时间段$$[ 1, ~ 4 ]$$内的平均速度为()
B
A.$${{2}{{m}{/}{s}}}$$
B.$${\frac{9} {4}} \mathrm{m / s}$$
C.$${\frac{1 1} {4}} \mathrm{m / s}$$
D.$${{3}{{m}{/}{s}}}$$
2、['平均变化率与函数的单调性']正确率60.0%已知$$f ( x )=2^{x}, \, \, \, g ( x )=3^{x}, \, \, \, h ( x )=x^{3},$$则在区间$$[ 1, \ 2 ]$$上函数值增长速度的大小顺序是()
C
A.$$h ( x ) < ~ f ( x ) < ~ g ( x )$$
B.$$h ( x ) < ~ g ( x ) < ~ f ( x )$$
C.$$f ( x ) < ~ g ( x ) < ~ h ( x )$$
D.$$g ( x ) < ~ f ( x ) < ~ h ( x )$$
3、['平均变化率与函数的单调性', '瞬时变化率']正确率60.0%已知函数$${{f}{(}{x}{)}}$$和$${{g}{(}{x}{)}}$$在区间$$[ a, ~ b ]$$上的图象如图所示,则下列说法正确的是()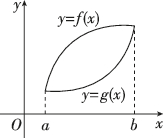
D
A.$${{f}{(}{x}{)}}$$在$$[ a, ~ b ]$$上的平均变化率大于$${{g}{(}{x}{)}}$$在$$[ a, ~ b ]$$上的平均变化率
B.$${{f}{(}{x}{)}}$$在$$[ a, ~ b ]$$上的平均变化率小于$${{g}{(}{x}{)}}$$在$$[ a, ~ b ]$$上的平均变化率
C.对于任意$$x_{0} \in( a, ~ b ),$$函数$${{f}{(}{x}{)}}$$在$${{x}{=}{{x}_{0}}}$$处的瞬时变化率总大于函数$${{g}{(}{x}{)}}$$在$${{x}{=}{{x}_{0}}}$$处的瞬时变化率
D.存在$$x_{0} \in( a, ~ b ),$$使得函数$${{f}{(}{x}{)}}$$在$${{x}{=}{{x}_{0}}}$$处的瞬时变化率小于函数$${{g}{(}{x}{)}}$$在$${{x}{=}{{x}_{0}}}$$处的瞬时变化率
4、['平均变化率与函数的单调性']正确率60.0%已知函数$$f ( x )=a x^{2}$$在区间$$[ 1, \ 2 ]$$上的平均变化率为$${\sqrt {3}{,}}$$则$${{f}{(}{x}{)}}$$在区间$$[-2, ~-1 ]$$上的平均变化率为()
A
A.$${{−}{\sqrt {3}}}$$
B.$${\sqrt {3}}$$
C.$$- \frac{\sqrt3} {3}$$
D.$$\frac{\sqrt{3}} {3}$$
5、['平均变化率与函数的单调性']正确率80.0%某质点沿直线运动的方程为$$f ( x )=-2 x^{2}+1 ( x$$表示时间表示位移$${{)}}$$,则该质点从$${{x}{=}{1}}$$到$${{x}{=}{2}}$$的平均速度为()
D
A.$${{−}{4}}$$
B.$${{−}{8}}$$
C.$${{6}}$$
D.$${{−}{6}}$$
6、['平均变化率与函数的单调性', '变化率']正确率80.0%函数$$f ( x )=\sqrt{x}$$在$$[ 0, \ 2 ]$$上的平均变化率为()
A
A.$$\frac{\sqrt2} {2}$$
B.$${{1}}$$
C.$${{0}}$$
D.$${{2}}$$
7、['平均变化率与函数的单调性']正确率80.0%如图,函数$$y=f ( x )$$在$${{A}{,}{B}}$$两点间的平均变化率等于()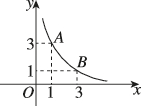
A
A.$${{−}{1}}$$
B.$${{1}}$$
C.$${{−}{2}}$$
D.$${{2}}$$
8、['平均变化率与函数的单调性', '导数的几何意义', '不等式比较大小']正确率40.0%设正弦函数$${{y}{=}{{s}{i}{n}}{x}}$$在$${{x}{=}{0}}$$和$$x=\frac{\pi} {2}$$附近的平均变化率为$${{k}_{1}{,}{{k}_{2}}}$$,则$${{k}_{1}{,}{{k}_{2}}}$$的大小关系为$${{(}{)}}$$
A
A.$${{k}_{1}{>}{{k}_{2}}}$$
B.$${{k}_{1}{<}{{k}_{2}}}$$
C.$${{k}_{1}{=}{{k}_{2}}}$$
D.不确定
9、['平均变化率与函数的单调性']正确率80.0%若函数$$y=a x+b$$在区间$$[ 1, 2 ]$$上的平均变化率为$${{3}}$$,则$${{a}{=}}$$()
C
A.$${{−}{3}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{−}{2}}$$
10、['平均变化率与函数的单调性']正确率60.0%已知函数$$f ( x )=-x^{2}+2 x$$,函数$${{f}{(}{x}{)}}$$从$${{2}}$$到$${{2}{+}{Δ}{x}}$$的平均变化率为$${{(}{)}}$$
B
A.$${{2}{−}{Δ}{x}}$$
B.$$- 2-\Delta x$$
C.$${{2}{+}{Δ}{x}}$$
D.$$( \Delta x ) 2-2 \cdot\Delta x$$
1. 解析:
平均速度公式为 $$\frac{s(4) - s(1)}{4 - 1}$$。
计算位移:
$$s(4) = \frac{1}{4} \times 4^2 + 4 = 4 + 4 = 8 \, \text{m}$$
$$s(1) = \frac{1}{4} \times 1^2 + 1 = \frac{1}{4} + 1 = \frac{5}{4} \, \text{m}$$
平均速度为 $$\frac{8 - \frac{5}{4}}{3} = \frac{\frac{27}{4}}{3} = \frac{9}{4} \, \text{m/s}$$。
正确答案:B。
2. 解析:
计算各函数在区间 $$[1, 2]$$ 上的平均增长率:
$$f(x) = 2^x$$ 的增长率为 $$\frac{2^2 - 2^1}{2 - 1} = 2$$。
$$g(x) = 3^x$$ 的增长率为 $$\frac{3^2 - 3^1}{2 - 1} = 6$$。
$$h(x) = x^3$$ 的增长率为 $$\frac{2^3 - 1^3}{2 - 1} = 7$$。
因此增长速度顺序为 $$f(x) < g(x) < h(x)$$。
正确答案:C。
3. 解析:
平均变化率为函数值的差与自变量差的比值。从图像可知,$$f(x)$$ 在 $$[a, b]$$ 上的变化幅度大于 $$g(x)$$,因此 $$f(x)$$ 的平均变化率更大。
瞬时变化率是导数,图像显示 $$f(x)$$ 的斜率在某些点小于 $$g(x)$$,因此 D 选项正确。
正确答案:D。
4. 解析:
平均变化率公式为 $$\frac{f(2) - f(1)}{2 - 1} = a(2^2 - 1^2) = 3a = \sqrt{3}$$,解得 $$a = \frac{\sqrt{3}}{3}$$。
在区间 $$[-2, -1]$$ 上,平均变化率为 $$\frac{f(-1) - f(-2)}{-1 - (-2)} = a((-1)^2 - (-2)^2) = -3a = -\sqrt{3}$$。
正确答案:A。
5. 解析:
平均速度为 $$\frac{f(2) - f(1)}{2 - 1} = (-2 \times 2^2 + 1) - (-2 \times 1^2 + 1) = (-8 + 1) - (-2 + 1) = -7 + 1 = -6$$。
正确答案:D。
6. 解析:
平均变化率为 $$\frac{f(2) - f(0)}{2 - 0} = \frac{\sqrt{2} - 0}{2} = \frac{\sqrt{2}}{2}$$。
正确答案:A。
7. 解析:
从图像可知,点 $$A(1, 3)$$ 和 $$B(3, 1)$$,平均变化率为 $$\frac{1 - 3}{3 - 1} = -1$$。
正确答案:A。
8. 解析:
计算平均变化率:
$$k_1 = \frac{\sin(0 + h) - \sin(0)}{h} \approx \cos(0) = 1$$(当 $$h \to 0$$)。
$$k_2 = \frac{\sin\left(\frac{\pi}{2} + h\right) - \sin\left(\frac{\pi}{2}\right)}{h} \approx \cos\left(\frac{\pi}{2}\right) = 0$$(当 $$h \to 0$$)。
因此 $$k_1 > k_2$$。
正确答案:A。
9. 解析:
平均变化率为 $$\frac{(2a + b) - (a + b)}{2 - 1} = a = 3$$。
正确答案:C。
10. 解析:
平均变化率为 $$\frac{f(2 + \Delta x) - f(2)}{\Delta x}$$。
计算:
$$f(2) = -4 + 4 = 0$$。
$$f(2 + \Delta x) = -(2 + \Delta x)^2 + 2(2 + \Delta x) = -4 - 4\Delta x - (\Delta x)^2 + 4 + 2\Delta x = -2\Delta x - (\Delta x)^2$$。
因此平均变化率为 $$\frac{-2\Delta x - (\Delta x)^2}{\Delta x} = -2 - \Delta x$$。
正确答案:B。
.jpg)