正确率40.0%
中国传统文化中很多内容体现了数学中的“对称美”, 太极图是由黑白两个鱼形纹组成的圆形图案,充分体现了相互转化、对称统一的形式美、和谐美 $${{.}}$$ 定义图象能够将圆 $${{O}{(}{O}}$$ 为坐标原点 $${{)}}$$ 的周长和面积同时等分成两部分的函数称为圆 $${{O}}$$ 的一个“太极函数”,给出下列命题:
$${①}$$ 对于任意一个圆 $${{O}}$$ ,其“太极函数”有无数个 $${{;}}$$
$${②}$$ 函数 $$f ( x )=\operatorname{l n} ( \sqrt{x^{2}+1}-x )$$ 可以是某个圆 $${{O}}$$ 的“太极函数” $${{;}}$$
$${③}$$ 函数 $$f ( x )=x^{\frac2 3}$$ 可以同时是无数个圆 $${{O}}$$ 的“太极函数” $${{;}}$$
$${④}$$ 函数 $$y=f ( x )$$ 是“太极函数”的充要条件为 $$y=f ( x )$$ 的图象是中心对称图形.
其中正确结论的序号是$${{(}{)}}$$
A.$${①{②}}$$
B.$${①{②}{④}}$$
C.$${①{③}}$$
D.$${①{④}}$$
2、['函数图象的识别', '函数的奇偶性']正确率80.0%函数$$y=\left( 3^{x}-3^{-x} \right) \operatorname{c o s} x$$在区间$$[-\frac{\pi} {2}, \frac{\pi} {2} ]$$的图象大致为$${{(}{)}}$$
A.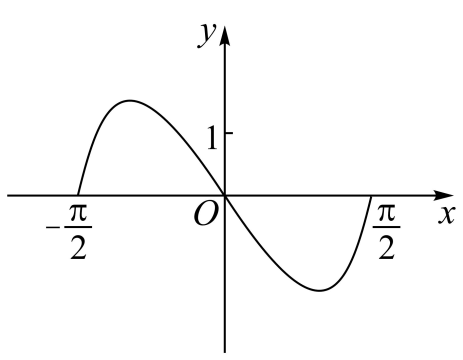
B.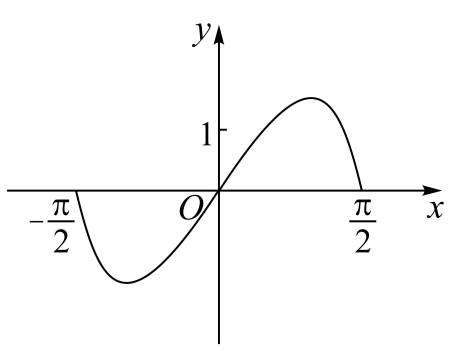
C.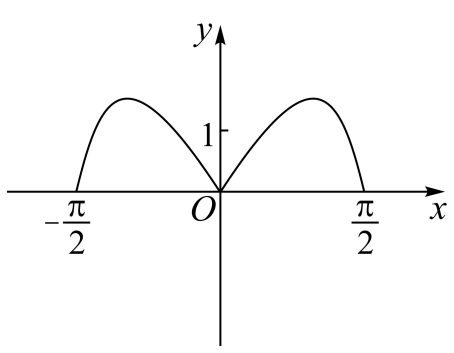
D.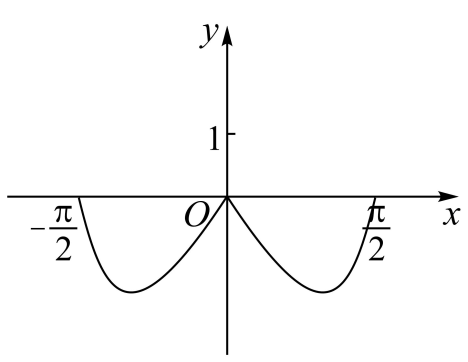
正确率80.0%已知定义在$${{R}}$$上的函数$${{f}{(}{x}{)}}$$满足$$f ( x+3 )=-f ( x )$$,$$g ( x )=f ( x )-2$$为奇函数,则$$f ( 1 9 8 )=( \textsubscript{\Lambda} )$$
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
4、['函数的基本性质', '函数的奇偶性', '函数的单调区间']正确率80.0%下列函数中,既是偶函数,又是在区间$$( 0,+\infty)$$上单调递减的是$${{(}{)}}$$
A.$${{y}{=}{{x}^{2}}}$$
B.$$y=2^{-| x |}$$
C.$${{y}{=}{\sqrt {x}}}$$
D.$$y=\operatorname{l o g}_{\frac1 2} \, x$$
5、['函数的奇偶性', '二次函数的图象分析与判断']正确率80.0%已知函数$$f ( x )=a x^{2}+b x+3 a+b$$是定义域为$$[ a-1, 2 a ]$$的偶函数,$${{a}{+}{b}}$$的值是$${{(}{)}}$$
A.$${{0}}$$
B.$$\frac{1} {3}$$
C.$${{1}}$$
D.$${{−}{1}}$$
6、['三角函数的图象与性质', '函数的奇偶性']正确率80.0%下列函数中,周期为$${{1}}$$的奇函数是$${{(}{)}}$$
A.$$y=1-\operatorname{s i n} x$$
B.$$y=-\operatorname{s i n} \pi x$$
C.$$y=\operatorname{s i n} \pi x \operatorname{c o s} \pi x$$
D.$$y=\operatorname{s i n} ( 2 \pi x+\frac{\pi} {3} )$$
7、['函数的奇偶性']正确率40.0%已知函数$${{f}{(}{x}{)}}$$的定义域为$${{R}}$$,若$$f ( 2 x+1 )$$为偶函数,$$f ( x+2 )$$为奇函数,则$${{(}{)}}$$
A.$$f (-1 )=0$$
B.$$f ( 1 )=0$$
C.$$f ( 2 0 2 2 )=0$$
D.$$f ( 2 0 2 3 )=0$$
8、['函数的奇偶性']正确率80.0%已知函数$$f ( x )=e^{2 x}+e^{-2 x+2}$$,则$${{(}{)}}$$
A.$$f ( x+1 )$$为奇函数
B.$$f ( x+\frac{1} {2} )$$为偶函数
C.$$f ( x-1 )$$为奇函数
D.$$f ( x-\frac{1} {2} )$$为偶函数
9、['函数的奇偶性']正确率80.0%如果偶函数$${{f}{(}{x}{)}}$$在$$[ 3, 7 ]$$上是增函数且最小值是$${{5}}$$,那么$${{f}{(}{x}{)}}$$在$$[-7,-3 ]$$上是$${{(}{)}}$$
A.增函数且最大值是$${{−}{5}}$$
B.减函数且最大值是$${{−}{5}}$$
C.增函数且最小值是$${{−}{5}}$$
D.减函数且最小值是$${{−}{5}}$$
10、['函数的奇偶性']正确率80.0%下列函数为偶函数的是$${{(}{)}}$$
A.$$y=| x |$$
B.$${{y}{=}{{l}{n}}{x}}$$
C.$${{y}{=}{{e}^{x}}}$$
D.$${{y}{=}{{x}^{3}}}$$
1. 解析:
② 错误。函数 $$f(x)=\ln(\sqrt{x^2+1}-x)$$ 是奇函数,但其图像不对称于原点,无法将圆的面积和周长同时等分。
③ 正确。函数 $$f(x)=x^{\frac{2}{3}}$$ 是奇函数,对于以原点为圆心的圆,可以满足“太极函数”的条件,且存在无数个这样的圆。
④ 错误。中心对称图形不一定能将圆的周长和面积同时等分,例如某些非对称函数也可能满足条件。
综上,正确选项为 $$C$$(①③)。
2. 解析:
3. 解析:
4. 解析:
5. 解析:
6. 解析:
7. 解析:
8. 解析:
9. 解析:
10. 解析:
.jpg)