正确率40.0%已知$${{f}{(}{x}{)}}$$是定义在区间$$[-7, ~ 7 ]$$上的偶函数,且其在$$[ 0, \ 7 ]$$上的图象如图所示,下列说法正确的是()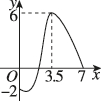
C
A.函数$${{f}{(}{x}{)}}$$有两个单调递增区间
B.函数$${{f}{(}{x}{)}}$$有两个单调递减区间
C.函数$${{f}{(}{x}{)}}$$在其定义域内有最大值$${{6}}$$
D.函数$${{f}{(}{x}{)}}$$在其定义域内有最小值$${{−}{6}}$$
2、['三角恒等变换综合应用', '函数y=A sin(wx+φ)(A≠0,w不等于0)的图象及性质', '函数的单调区间']正确率60.0%函数$$y=\operatorname{s i n}^{2} x+2 \operatorname{s i n} x \operatorname{c o s} x+3 \operatorname{c o s}^{2} x$$在$$x \in( 0, \, \, \frac{\pi} {2} )$$的单调递增区间是()
C
A.$$( 0, ~ \frac{\pi} {4} )$$
B.$$( \frac{\pi} {4}, \ \frac{\pi} {2} )$$
C.$$( 0, ~ \frac{\pi} {8} )$$
D.$$( \frac{\pi} {8}, \ \frac{\pi} {4} )$$
3、['简单复合函数的导数', '正弦(型)函数的单调性', '基本初等函数的导数', '导数与单调性', '函数的单调区间']正确率40.0%已知函数$$f ( x )=\operatorname{s i n} ( 2 x+\frac{\pi} {1 2} )$$,则函数$$y=2 f ( x )+f^{\prime} ( x )$$的一个单调递减区间是$${{(}{)}}$$
A
A.$$[ \frac{\pi} {1 2}, \frac{7 \pi} {1 2} ]$$
B.$$[-\frac{5 \pi} {1 2}, \frac{\pi} {1 2} ]$$
C.$$[-\frac{\pi} {3}, \frac{2 \pi} {3} ]$$
D.$$[-\frac{\pi} {6}, \frac{5 \pi} {6} ]$$
4、['函数的对称性', '函数的单调区间', '等差数列的前n项和的应用', '等差数列的性质']正确率40.0%已知函数$$y=f ~ ( x )$$对任意自变量$${{x}}$$都有$$f \left( \begin{matrix} {\alpha} \\ {\alpha} \\ \end{matrix} \right)=f \left( \begin{matrix} {2-\alpha} \\ \end{matrix} \right)$$,且函数$${{f}{(}{x}{)}}$$在$$[ 1, ~+\infty)$$上单调.若数列$${{\{}{{a}_{n}}{\}}}$$是公差不为$${{0}}$$的等差数列,且$$f \ ( \ a_{6} ) \ =\ f \ ( \ a_{2 0 1 2} )$$,则$${{\{}{{a}_{n}}{\}}}$$的前$${{2}{0}{1}{7}}$$项之和为()
B
A.$${{0}}$$
B.$${{2}{0}{1}{7}}$$
C.$${{2}{0}{1}{6}}$$
D.$${{4}{0}{3}{4}}$$
5、['函数奇偶性的应用', '函数的单调区间', '不等式比较大小']正确率40.0%已知函数$${{f}{{(}{x}{)}}}$$是定义在$${{R}}$$上的偶函数,在$$(-\infty, 0 ]$$上有单调性,且$$f \left(-2 \right) < f \left( 1 \right)$$,则下列不等式成立的是$${{(}{)}}$$
D
A.$$f \left(-1 \right) < f \left( 2 \right) < f \left( 3 \right)$$
B.$$f \left( 2 \right) < f \left( 3 \right) < f \left(-4 \right)$$
C.$$f \left(-2 \right) < f \left( 0 \right) < f \left( \frac1 2 \right)$$
D.$$f \left( 5 \right) < f \left(-3 \right) < f \left(-1 \right)$$
6、['抽象函数的应用', '函数奇、偶性的定义', '命题的真假性判断', '函数的单调区间', '函数求定义域']正确率40.0%给出下列说法:
$${①}$$若函数$${{f}{{(}{x}{)}}}$$的定义域为$$[ 0, 2 ] \;,$$则函数$${{f}{{(}{2}{x}{)}}}$$的定义域为$$[ 0, 4 ] \; ;$$
$${②}$$函数$$y=\frac{1} {x^{2}}$$的单调减区间是$$(-\infty, 0 ), ~ ~ ( 0,+\infty)$$;
$${③}$$不存在实数$${{m}}$$,使$$f \left( x \right)=x^{2}+m x+1$$为奇函数;
$${④}$$若$$f \left( x+y \right)=f ( x ) f ( y )$$,且$${{f}{{(}{1}{)}}{=}{2}}$$,则$$\frac{f \left( 2 \right)} {f \left( 1 \right)}+\frac{f \left( 4 \right)} {f \left( 3 \right)}+\ldots+\frac{f \left( 2 0 1 6 \right)} {f \left( 2 0 1 5 \right)}=2 0 1 6.$$
其中正确说法的序号是()
D
A.$${①{③}}$$
B.$${②{③}}$$
C.$${②{④}}$$
D.$${③{④}}$$
7、['函数奇偶性的应用', '导数与单调性', '单调性的定义与证明', '函数奇、偶性的定义', '利用导数讨论函数单调性', '函数单调性的判断', '函数的单调区间']正确率40.0%设$$F \mid x \mid=\frac{f ( x )} {g ( x )}$$是$$( \mathbf{-} \infty, \ \mathbf{0} ) \ \cup\ ( \mathbf{0}, \ \mathbf{+} \infty)$$上的偶函数,当$${{x}{<}{0}}$$时,$$f^{\prime} \, \, ( \textbf{x} ) \, \, g \, ( \textbf{x} ) \, \,-f \, ( \textbf{x} ) \, \, \, g^{\prime} \, \, ( \textbf{x} ) \, \, > 0$$,且$$f \ ( \ 2 ) \ =0$$,则不等式$$F \ ( \textbf{x} ) \ < 0$$的解集是()
C
A.$$( \mathbf{\theta}-2, \ \mathbf{0} ) \cup\ ( \mathbf{2}, \ \mathbf{\theta}+\infty)$$
B.$$( \mathbf{\alpha}-2, \ \mathbf{0} ) \ \cup\ ( \mathbf{0}, \ \mathbf{2} )$$
C.$$( \mathbf{\tau}-\infty, \mathbf{\tau}-\mathbf{2} ) \cup\mathbf{\tau} ( \mathbf{2}, \mathbf{\tau}+\infty)$$
D.$$( \mathbf{\theta}-\infty, \mathbf{\theta}-2 ) \ \cup\ ( \mathbf{0}, \ 2 )$$
8、['导数的四则运算法则', '基本初等函数的导数', '导数与单调性', '函数的单调区间']正确率60.0%函数$${{y}{=}{x}{{e}^{x}}}$$的单调减区间是()
B
A.$$( \mathrm{~-\infty, \ 1 ~} )$$
B.$$( \ -\infty, \ -1 )$$
C.$$( 1, ~+\infty)$$
D.$$( \ -1, \ \ +\infty)$$
9、['利用导数讨论函数单调性', '根据函数零点个数求参数范围', '函数的单调区间', '函数零点存在定理']正确率19.999999999999996%已知函数$$f \left( x \right)=\frac{1} {4} a x^{4}-x^{3}+x+2 0 1 9, \, \, \, f^{\prime} \left( x \right)$$是$${{f}{{(}{x}{)}}}$$的导函数,若$${{f}{^{′}}{{(}{x}{)}}}$$存在唯一的零点$${{x}_{0}}$$,且$$x_{0} \in( 0,+\infty)$$,则实数$${{a}}$$的取值范围是()
A
A.$$(-\infty,-2 )$$
B.$$(-\infty,-1 )$$
C.$$( 1,+\infty)$$
D.$$( 2,+\infty)$$
10、['函数单调性的判断', '函数的单调区间']正确率60.0%下列函数中,在区间$$[ 2, ~ 4 ]$$上为增函数的是()
C
A.$$y=\frac{1} {x-1}$$
B.$${{y}{=}{−}{{x}^{2}}}$$
C.$$y=l n x$$
D.$$y=~ ( \frac{1} {2} ) ~^{x}$$
1. 解析:
由于 $$f(x)$$ 是偶函数,其在 $$[-7, 0]$$ 上的图像与 $$[0, 7]$$ 对称。根据图像,$$f(x)$$ 在 $$[0, 7]$$ 上有两个单调递增区间和两个单调递减区间,因此在整个定义域内共有四个单调区间(A、B 均不完整)。最大值在 $$x=0$$ 处取得,为 $$6$$(C 正确),但最小值无法确定是否为 $$-6$$(D 错误)。
答案:C
2. 解析:
化简函数:
$$y = \sin^2 x + 2 \sin x \cos x + 3 \cos^2 x = 1 + \sin 2x + 2 \cos^2 x = 2 + \sin 2x + \cos 2x = 2 + \sqrt{2} \sin(2x + \frac{\pi}{4})$$。
求导得 $$y' = 2\sqrt{2} \cos(2x + \frac{\pi}{4})$$。令 $$y' > 0$$,解得 $$\cos(2x + \frac{\pi}{4}) > 0$$,即 $$2x + \frac{\pi}{4} \in (-\frac{\pi}{2} + 2k\pi, \frac{\pi}{2} + 2k\pi)$$。在 $$x \in (0, \frac{\pi}{2})$$ 时,单调递增区间为 $$(0, \frac{\pi}{8})$$。
答案:C
3. 解析:
设 $$f(x) = \sin(2x + \frac{\pi}{12})$$,则 $$f'(x) = 2 \cos(2x + \frac{\pi}{12})$$。
$$y = 2f(x) + f'(x) = 2 \sin(2x + \frac{\pi}{12}) + 2 \cos(2x + \frac{\pi}{12}) = 2\sqrt{2} \sin(2x + \frac{\pi}{12} + \frac{\pi}{4}) = 2\sqrt{2} \sin(2x + \frac{\pi}{3})$$。
求单调递减区间:令 $$\frac{\pi}{2} + 2k\pi \leq 2x + \frac{\pi}{3} \leq \frac{3\pi}{2} + 2k\pi$$,解得 $$\frac{\pi}{12} + k\pi \leq x \leq \frac{7\pi}{12} + k\pi$$。选项 A 符合 $$k=0$$ 的情况。
答案:A
4. 解析:
由题意 $$f(\alpha) = f(2 - \alpha)$$,对称轴为 $$x = 1$$。又 $$f(x)$$ 在 $$[1, +\infty)$$ 上单调,故 $$f(x)$$ 在 $$(-\infty, 1]$$ 上也单调(偶函数性质)。
由 $$f(a_6) = f(a_{2012})$$ 及对称性,得 $$a_6 + a_{2012} = 2$$。等差数列中 $$a_6 + a_{2012} = 2a_{1009}$$,故 $$a_{1009} = 1$$。
前 $$2017$$ 项和为 $$S_{2017} = 2017 \cdot a_{1009} = 2017$$。
答案:B
5. 解析:
偶函数 $$f(x)$$ 在 $$(-\infty, 0]$$ 上有单调性且 $$f(-2) < f(1)$$,说明 $$f(x)$$ 在 $$(-\infty, 0]$$ 上单调递减,在 $$[0, +\infty)$$ 上单调递增。
比较函数值:
- $$f(5) = f(-5)$$,$$f(-3)$$,$$f(-1)$$ 随自变量减小而增大,故 $$f(5) < f(-3) < f(-1)$$(D 正确)。
答案:D
6. 解析:
① 错误,$$f(2x)$$ 定义域为 $$[0, 1]$$;
② 错误,单调减区间应为 $$(-\infty, 0)$$ 和 $$(0, +\infty)$$,但不能并起来;
③ 正确,二次函数不可能为奇函数;
④ 正确,由 $$f(x+y) = f(x)f(y)$$ 得 $$f(x) = 2^x$$,故 $$\frac{f(2k)}{f(2k-1)} = 2$$,求和为 $$2016 \times 1 = 2016$$。
答案:D
7. 解析:
设 $$F(x) = \frac{f(x)}{g(x)}$$ 为偶函数,且 $$x < 0$$ 时 $$F'(x) = \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} > 0$$,故 $$F(x)$$ 在 $$(-\infty, 0)$$ 上单调递增,在 $$(0, +\infty)$$ 上单调递减。
由 $$f(2) = 0$$ 得 $$F(2) = 0$$,且 $$F(-2) = 0$$。不等式 $$F(x) < 0$$ 的解集为 $$(-2, 0) \cup (2, +\infty)$$。
答案:A
8. 解析:
求导 $$y' = e^x + x e^x = e^x (1 + x)$$。令 $$y' < 0$$,得 $$1 + x < 0$$,即 $$x < -1$$。单调减区间为 $$(-\infty, -1)$$。
答案:B
9. 解析:
$$f'(x) = a x^3 - 3x^2 + 1$$,设唯一零点 $$x_0 \in (0, +\infty)$$,则 $$f'(x)$$ 在 $$x_0$$ 处取得极值且 $$f'(x_0) = 0$$。
由三次函数性质,需 $$f'(x)$$ 在 $$x_0$$ 处为极小值且 $$f'(0) = 1 > 0$$。代入 $$x_0$$ 得 $$a x_0^3 - 3x_0^2 + 1 = 0$$,且 $$3a x_0^2 - 6x_0 = 0$$(导数为零)。解得 $$x_0 = \frac{2}{a}$$,代入得 $$a = -2$$。为使 $$x_0 > 0$$,需 $$a < 0$$,且唯一极小值点要求 $$a < -2$$。
答案:A
10. 解析:
A. $$y = \frac{1}{x-1}$$ 在 $$[2, 4]$$ 上单调递减;
B. $$y = -x^2$$ 在 $$[2, 4]$$ 上单调递减;
C. $$y = \ln x$$ 在 $$[2, 4]$$ 上单调递增;
D. $$y = (\frac{1}{2})^x$$ 在 $$[2, 4]$$ 上单调递减。
答案:C
.jpg)