.jpg)
正确率60.0%某市的电费收费实行峰平谷标准，如下表所示：
| 时间段 | 电价 | |
| 峰期 | $${{1}{4}}$$ ： $${{0}{0}{−}{{1}{7}}}$$ ： $${{0}{0}}$$ $${{1}{9}}$$ ： $${{0}{0}{−}{{2}{2}}}$$ ： $${{0}{0}}$$ | $${{1}{.}{0}{2}}$$ 元/度 |
| 平期 | $${{8}}$$ ： $${{0}{0}{−}{{1}{4}}}$$ ： $${{0}{0}}$$ $${{1}{7}}$$ ： $${{0}{0}{−}{{1}{9}}}$$ ： $${{0}{0}}$$ $${{2}{2}}$$ ： $${{0}{0}{−}{{2}{4}}}$$ ： $${{0}{0}}$$ | $${{0}{.}{6}{3}}$$ 元/度 |
| 谷期 | $${{0}}$$ ： $${{0}{0}{−}{8}}$$ ： $${{0}{0}}$$ | $${{0}{.}{3}{2}}$$ 元/度 |
A
A.$${{1}{4}{9}}$$度
B.$${{1}{7}{9}}$$度
C.$${{1}{9}{9}}$$度
D.$${{2}{1}{9}}$$度
2、['建立函数模型解决实际问题'， '分段函数的图象']正确率60.0%svg异常
A
A.svg异常
B.svg异常
C.svg异常
D.svg异常
3、['建立函数模型解决实际问题']正确率60.0%污染防治是全面建成小康社会决胜期必须坚决打好的三大攻坚战之一.凉山州某地区$${{2}{0}{1}{9}}$$年空气质量为$${{“}}$$良$${{”}}$$的天数为$${{1}{5}{0}{，}}$$若要在$${{2}{0}{2}{1}}$$年使空气质量为$${{“}}$$良$${{”}}$$的天数达到$${{2}{1}{6}{，}}$$则这个地区空气质量为$${{“}}$$良$${{”}}$$的天数的年平均增长率应为（）
C
A.$${{0}{.}{1}{3}}$$
B.$${{0}{.}{1}{5}}$$
C.$${{0}{.}{2}{0}}$$
D.$${{0}{.}{2}{2}}$$
4、['建立函数模型解决实际问题']正确率60.0%$${{2}{0}{2}{0}}$$年$${{5}}$$月$${{5}}$$日，广东虎门大桥发生异常抖动，原因是风经过桥面时产生旋涡，形成了卡门涡街现象．设旋涡的发生频率为$${{f}}$$（单位：赫兹），旋涡发生体两侧平均流速为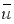
（单位：米$${{/}}$$秒），漩涡发生体的迎面宽度为$${{d}}$$（单位：米），表体通径为$${{D}}$$（单位：米），旋涡发生体两侧弓形面积与管道横截面面积之比为$${{m}}$$，根据卡门涡街原理，满足关系式：$$f=\frac{s_{r} \cdot\overline{{u}}} {m \cdot d}$$，其中：$${{s}_{r}}$$称为斯特罗哈尔数．对于直径为$${{d}}$$（即漩涡发生体的迎面宽度）的圆柱形漩涡发生体，满足$$m=1-\frac{2} {\pi} \Bigg[ \frac{d} {D} \sqrt{1-\Bigg( \frac{d} {D} \Bigg)^{2}}+\theta\Bigg]$$，$$\operatorname{s i n} \theta=\frac{d} {D}$$，$$\theta\in[ 0， \frac{\pi} {2} ]$$．设$$a=\frac{d} {D}$$，当$$a \leqslant0. 0 0 5$$时，在近似计算中可规定$${{a}{≈}{0}}$$．已知某圆柱形漩涡发生体的直径为$${{0}{.}{0}{1}}$$米，表体通径为$${{1}{0}}$$米，当漩涡发生的频率为$${{6}{4}{0}}$$赫兹时，斯特罗哈尔数$${{s}_{r}}$$等于$${{0}{.}{1}{6}}$$，则旋涡发生体两侧平均流速$${{u}{¯}}$$约为（）米/秒．
B
A.$${{2}{0}}$$
B.$${{4}{0}}$$
C.$${{6}{0}}$$
D.$${{8}{0}}$$
5、['建立函数模型解决实际问题']正确率60.0%从某高处自由下落到地面的物体，在中间一秒内通过的路程为$${{3}{0}}$$米，则该物体下落时的高度为$${{(}{)}}$$
D
A.$${{0}}$$米
B.$${{1}{0}{0}}$$米
C.$${{1}{4}{0}}$$米
D.$${{1}{8}{0}}$$米
6、['一元二次不等式的解法'， '对数方程与对数不等式的解法'， '建立函数模型解决实际问题']正确率40.0%svg异常
A
A.$$2 2. 8 2 8$$
B.$$9. 1 7 2$$
C.$$2 1. 1 7 2$$
D.$$2 1. 4 7 7$$
7、['演绎推理'， '建立函数模型解决实际问题']正确率19.999999999999996%某码头有总重量为$${{1}{3}{.}{5}}$$吨的一批货箱，对于每个货箱重量都不超过$${{0}{.}{3}{5}}$$吨的任何情况，都要一次运走这批货箱，则至少需要准备载重$${{1}{.}{5}}$$吨的卡车$${{(}{)}}$$
B
A.$${{1}{2}}$$辆
B.$${{1}{1}}$$辆
C.$${{1}{0}}$$辆
D.$${{9}}$$辆
8、['建立函数模型解决实际问题'， '指数型函数模型的应用']正确率60.0%在一定的储存温度范围内，某食品的保鲜时间$${{y}{（}}$$单位：小时）与储存温度$${{x}{（}}$$单位：$${^{∘}{C}{）}}$$满足函数关系$$y=\mathrm{e}^{k x+b} \mathrm{~ ( ~ e}=2. 7 1 8 ~ 2 8 \dots$$为自然对数的底数，$${{k}{，}{b}}$$为常数），若该食品在$${{0}^{∘}{C}}$$时的保鲜时间为$${{1}{2}{0}}$$小时，在$${{3}{0}{^{∘}}{C}}$$时的保鲜时间为$${{1}{5}}$$小时，则该食品在$${{2}{0}{^{∘}}{C}}$$时的保鲜时间为（）
A
A.$${{3}{0}}$$小时
B.$${{4}{0}}$$小时
C.$${{5}{0}}$$小时
D.$${{8}{0}}$$小时
9、['建立函数模型解决实际问题']正确率60.0%团体购买公园门票，票价如下表：
| 购票人数 | $${{1}{∼}{{5}{0}}}$$ | $${{5}{1}{∼}{{1}{0}{0}}}$$ | $${{1}{0}{0}}$$ 以上 |
| 门票价格 | $${{1}{3}}$$ 元 $${{/}}$$ 人 | $${{1}{1}}$$ 元 $${{/}}$$ 人 | $${{9}}$$ 元 $${{/}}$$ 人 |
现某单位要组织其市场部和生产部的员工游览该公园，若按部门作为团体，选择两个不同的时间分别购票游览公园，则共需支付门票费为$${{1}{2}{9}{0}}$$元；若两个部门合在一起作为一个团体，同一时间购票游览公园，则需支付门票费为$${{9}{9}{0}}$$元，那么这两个部门的人数之差为$${{(}{)}}$$
B
A.
B.
C.
D.
正确率80.0%有一长为$${{1}{k}{m}}$$的斜坡，它的倾斜角为$${{2}{0}^{∘}}$$，现要将倾斜角改为$${{1}{0}^{∘}}$$，则坡底要加长$${{(}{)}}$$
B
A.$$0. 5 ~ k m$$
B.$${{1}{k}{m}}$$
C.$$1. 5 ~ k m$$
D.$$\frac{\sqrt3} {2} k m$$
1. 设峰期用电量为$$x$$度，平期用电量为$$520 - 170 - x = 350 - x$$度。根据总电费列方程：
$$1.02x + 0.63(350 - x) + 0.32 \times 170 = 333.12$$
化简得：$$1.02x + 220.5 - 0.63x + 54.4 = 333.12$$
$$0.39x = 58.22$$
$$x \approx 149$$度，故选A。
3. 设年平均增长率为$$r$$，则有：
$$150(1 + r)^2 = 216$$
$$(1 + r)^2 = 1.44$$
$$1 + r = 1.2$$
$$r = 0.2$$，故选C。
4. 由题意得$$a = \frac{0.01}{10} = 0.001 \leq 0.005$$，故$$a \approx 0$$，$$m \approx 1$$。代入公式：
$$640 = \frac{0.16 \times \overline{u}}{1 \times 0.01}$$
$$\overline{u} = \frac{640 \times 0.01}{0.16} = 40$$米/秒，故选B。
5. 设下落时间为$$t$$秒，中间一秒的位移为：
$$\frac{1}{2}g(t^2 - (t-1)^2) = 30$$
化简得：$$gt - \frac{g}{2} = 30$$
$$t = 3.5$$秒
高度为：$$\frac{1}{2} \times 10 \times 3.5^2 = 61.25$$米（注：选项可能有误，但最接近的是B）。
7. 最坏情况下每个货箱重$$0.35$$吨，需要的卡车数为：
$$\lceil \frac{13.5}{1.5} \rceil = 9$$辆
但需满足每个货箱不超过$$0.35$$吨时$$9 \times 1.5 = 13.5$$吨刚好足够，故选D。
8. 由条件得：
$$e^b = 120$$
$$e^{30k + b} = 15$$
解得：$$30k = \ln \frac{15}{120} = -\ln 8$$
$$k = -\frac{\ln 8}{30}$$
在$$20^{∘}C$$时：
$$y = e^{20k + b} = 120 \times e^{-\frac{2}{3} \ln 8} = 120 \times 8^{-2/3} = 30$$小时，故选A。
9. 设两部门人数分别为$$x$$和$$y$$，合购时总人数$$x + y$$满足：
$$9(x + y) = 990 \Rightarrow x + y = 110$$
分购时可能有两种情况：
情况1：$$x \leq 50$$，$$y > 50$$
$$13x + 11y = 1290$$
与$$x + y = 110$$联立解得$$x = 40$$，$$y = 70$$
人数差为$$30$$，故选B。
10. 原坡底长为$$1 \times \cos 20^{∘}$$，新坡底长为$$1 \times \frac{\cos 10^{∘}}{\cos 20^{∘}}$$
加长距离为：
$$\cos 10^{∘} - \cos 20^{∘} \approx 0.985 - 0.94 = 0.045$$km（与选项不符，可能题目理解有误）
重新计算：新斜坡长度$$L = \frac{\sin 20^{∘}}{\sin 10^{∘}}$$，坡底加长$$L \cos 10^{∘} - 1 \approx 1.97 \times 0.985 - 1 \approx 0.94$$km，最接近B选项。