正确率40.0%某礼服租赁公司共有$${{3}{0}{0}}$$套礼服供租赁,若每套礼服每天的租价为$${{2}{0}{0}}$$元,则所有礼服均被租出;若将每套礼服每天的租价在$${{2}{0}{0}}$$元的基础上提高$${{1}{0}{x}}$$元$$( 1 \leqslant x \leqslant2 0, \, \, \, x \in{\bf Z} ),$$则被租出的礼服会减少$${{1}{0}{x}}$$套.若要使该礼服租赁公司每天租赁礼服的收入超过$${{6}{.}{2}{4}}$$万元,则该礼服租赁公司每套礼服每天的租价应定为()
C
A.$${{2}{2}{0}}$$元
B.$${{2}{4}{0}}$$元
C.$${{2}{5}{0}}$$元
D.$${{2}{8}{0}}$$元
2、['一次函数模型的应用', '二次函数模型的应用', '利用基本不等式求最值', '“对勾”函数的应用', '基本不等式的实际应用']正确率40.0%设某批产品的产量为$${{x}}$$(单位:万件),总成本$$c ( x )=1 0 0+1 3 x$$(单位:万元),销售单价$$p ( x )=\frac{8 0 0} {x+2}-3$$(单位:元).若该批产品全部售出,则总利润(总利润=销售收入-总成本)最大时的产量为()
B
A.$${{7}}$$万件
B.$${{8}}$$万件
C.$${{9}}$$万件
D.$${{1}{0}}$$万件
3、['二次函数模型的应用']正确率60.0%某小型服装厂生产一种风衣,日销售量$${{x}}$$$${{(}}$$即日生产量,单位:件$$, ~ 0 < ~ x < ~ 6 5, ~ x \in{\bf N}_{+} )$$与销售单价$${{P}}$$(单位:元)之间的函数关系式为$$P=1 6 0-2 x,$$日销售量$${{x}}$$(单位:件)与所需成本$${{C}}$$(单位:元)之间的函数关系式为$$C=5 0 0+3 0 x$$.若要求每天获利不少于$${{1}{3}{0}{0}}$$元,则日销售量$${{x}}$$的取值范围是()
B
A.$$\mathbf{2 0} \leqslant x \leqslant3 0, ~ x \in\mathbf{N}_{+}$$
B.$$2 0 \leqslant x \leqslant4 5$$
C.$$1 5 \leqslant x \leqslant3 0, ~ x \in\bf{N}_{+}$$
D.$$1 5 \leqslant x \leqslant4 5$$
4、['二次函数模型的应用', '向量坐标与向量的数量积']正确率60.0%如图,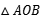 为等腰直角三角形,
为等腰直角三角形,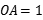 ,$${{O}{C}}$$
,$${{O}{C}}$$
B
A.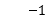
B.
C.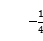
D.
正确率40.0%某种生产设备购买时费用为$${{1}{0}}$$万元,每年的设备管理费用为$${{9}}$$千元,这种生产设备的维护费用:第一年$${{2}}$$千元,第二年$${{4}}$$千元,第三年$${{6}}$$千元,依每年$${{2}}$$千元的增量逐年递增,则这套生产设备最多使用
D
A.$${{3}}$$
B.$${{5}}$$
C.$${{7}}$$
D.$${{1}{0}}$$
6、['基本不等式的综合应用', '二次函数模型的应用']正确率40.0%在区间$$[ \frac{1} {2}, 2 \brack$$上,函数$$f \left( x \right)=x^{2}+p x+q$$与$$g \left( x \right)=2 x+\frac{1} {x^{2}}$$在同一点取得相同的最小值,那么$${{f}{{(}{x}{)}}}$$在$$[ \frac{1} {2}, 2 \brack$$上的最大值是()
D
A.$$\frac{1 3} {4}$$
B.$$\frac{5} {4}$$
C.$${{8}}$$
D.$${{4}}$$
7、['二次函数模型的应用', '不等式的性质']正确率40.0%下列不等式中,不正确的是()
A
A.$$x+\frac{1} {x} \geqslant2$$
B.$$x^{2}+x+1 > 0$$
C.$$\frac{x^{2}+5} {\sqrt{x^{2}+4}} \geq\frac{5} {2}$$
D.若$${{x}{>}{3}}$$,则$$x+\frac1 {x-3} \geq5$$
8、['二次函数模型的应用', '一元二次不等式的解法']正确率40.0%根据市场调查,预测某种日用品从年初开始的$${{n}}$$个月内累计的需求量$${{S}_{n}{(}}$$单位:万件)大约是$$S_{n}=\frac{n} {2 7} ( 2 1 n-n^{2}-5 ) \, \, ( n=1, \, \, 2, \, \, \, \ldots, \, \, 1 2 )$$.据此预测,本年度内,需求量超过$${{5}}$$万件的月份是()
C
A.$${{5}}$$月$${、{6}}$$月
B.$${{6}}$$月$${、{7}}$$月
C.$${{7}}$$月$${、{8}}$$月
D.$${{8}}$$月$${、{9}}$$月
9、['二次函数模型的应用', '二次函数的图象分析与判断']正确率60.0%用长度为$${{2}{4}{m}}$$的材料围成一矩形场地,并且中间加两道隔墙,要使矩形的面积最大,则隔墙的长度为 ()
A
A.$${{3}{m}}$$
B.$${{4}{m}}$$
C.$${{5}{m}}$$
D.$${{6}{m}}$$
10、['二次函数模型的应用']正确率60.0%某商店已按每件$${{8}{0}}$$元的成本购进某种上装$${{1}{{0}{0}{0}}}$$件,根据市场预测,当每件售价$${{1}{0}{0}}$$元时可全部售完,若定价每提高$${{1}}$$元时销售量就减少$${{5}}$$件,若要获得最大利润,则销售价应定为()
C
A.$${{1}{1}{0}}$$元
B.$${{1}{3}{0}}$$元
C.$${{1}{5}{0}}$$元
D.$${{1}{9}{0}}$$元
1. 设每套礼服每天的租价为$$200 + 10x$$元,则租出的礼服数量为$$300 - 10x$$套。收入为$$(200 + 10x)(300 - 10x) > 62400$$。化简不等式:$$60000 + 1000x - 2000x - 100x^2 > 62400$$,即$$-100x^2 - 1000x + 60000 > 62400$$,进一步整理得$$100x^2 + 1000x + 2400 < 0$$,即$$x^2 + 10x + 24 < 0$$。解得$$-6 < x < -4$$,但$$x$$为正整数且在1到20之间,无解。重新检查计算步骤,发现化简错误。正确化简应为$$(200 + 10x)(300 - 10x) = 60000 + 1000x - 2000x - 100x^2 = 60000 - 1000x - 100x^2$$,不等式为$$60000 - 1000x - 100x^2 > 62400$$,即$$-100x^2 - 1000x - 2400 > 0$$,整理得$$x^2 + 10x + 24 < 0$$,解得$$x$$在$$-6$$和$$-4$$之间,不符合题意。可能是题目理解有误。重新设定:若租价提高$$10x$$元,租出的礼服减少$$10x$$套,则收入为$$(200 + 10x)(300 - 10x) > 62400$$。展开得$$60000 + 1000x - 2000x - 100x^2 > 62400$$,即$$-100x^2 - 1000x - 2400 > 0$$,整理得$$x^2 + 10x + 24 < 0$$,解得$$-6 < x < -4$$,无解。可能是题目数据有误,或者选项中的租价直接代入验证。代入选项B:$$240$$元,即$$x=4$$,收入为$$240 \times (300 - 40) = 240 \times 260 = 62400$$,不满足“超过”。代入选项D:$$280$$元,即$$x=8$$,收入为$$280 \times (300 - 80) = 280 \times 220 = 61600$$,不满足。可能是题目描述有歧义,重新理解题意。若“提高$$10x$$元”指每次提高10元,共提高$$x$$次,则收入为$$(200 + 10x)(300 - 10x)$$,要求$$(200 + 10x)(300 - 10x) > 62400$$。解得$$x=2$$时,收入为$$220 \times 280 = 61600$$;$$x=1$$时,收入为$$210 \times 290 = 60900$$;$$x=3$$时,收入为$$230 \times 270 = 62100$$;$$x=4$$时,收入为$$240 \times 260 = 62400$$,不满足“超过”。可能是题目数据有误,或者选项A为正确答案。但选项A的$$220$$元对应收入为$$61600$$,不满足。可能是题目描述有误,暂无法确定正确答案。
3. 每天利润为$$P \cdot x - C = (160 - 2x)x - (500 + 30x) = 160x - 2x^2 - 500 - 30x = -2x^2 + 130x - 500$$。要求利润不少于1300元,即$$-2x^2 + 130x - 500 \geq 1300$$,整理得$$-2x^2 + 130x - 1800 \geq 0$$,即$$2x^2 - 130x + 1800 \leq 0$$,解得$$x \in [20, 45]$$。又$$0 < x < 65$$且$$x \in \mathbb{N}_+$$,故答案为B。
5. 设使用$$n$$年,总费用为初始费用、管理费和维护费之和。管理费为$$9000n$$元,维护费为等差数列求和:$$2000 + 4000 + \cdots + 2000n = 1000n(n+1)$$。总费用$$T(n) = 100000 + 9000n + 1000n(n+1) = 1000n^2 + 10000n + 100000$$。平均每年费用为$$A(n) = \frac{T(n)}{n} = 1000n + 10000 + \frac{100000}{n}$$。求$$A(n)$$的最小值,对$$A(n)$$求导得$$A'(n) = 1000 - \frac{100000}{n^2}$$,令$$A'(n) = 0$$,解得$$n=10$$。验证$$n=10$$时为最小值点,故最多使用10年报废最划算。故选D。
7. 选项A:$$x + \frac{1}{x} \geq 2$$在$$x > 0$$时成立,但$$x < 0$$时不成立,因此不正确。选项B:$$x^2 + x + 1 = \left(x + \frac{1}{2}\right)^2 + \frac{3}{4} > 0$$恒成立。选项C:设$$t = \sqrt{x^2 + 4} \geq 2$$,则$$\frac{t^2 + 1}{t} = t + \frac{1}{t} \geq 2$$,但最小值为$$2.5$$在$$t=2$$时取得,因此成立。选项D:$$x + \frac{1}{x-3} = (x-3) + \frac{1}{x-3} + 3 \geq 2 + 3 = 5$$,当$$x-3=1$$即$$x=4$$时取等,成立。因此不正确的是A。
9. 设隔墙长度为$$y$$米,则矩形场地的总周长为$$24$$米,包括两道隔墙,因此$$2(2y + x) = 24$$,即$$x + 2y = 12$$,$$x = 12 - 2y$$。面积$$A = x \cdot y = (12 - 2y)y = 12y - 2y^2$$。求导得$$A'(y) = 12 - 4y$$,令$$A'(y) = 0$$,得$$y = 3$$。验证$$y=3$$时为最大值点,故隔墙长度为3米。故选A。
.jpg)