.jpg)
正确率40.0%
是$${{“}}$$函数$$y=2 x^{2}-m x+1$$在
内存在零点$${{”}}$$的（）
A
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
2、['利用函数单调性解不等式'， '二次函数模型的应用'， '导数与单调性'， '利用导数讨论函数单调性']正确率40.0%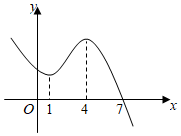
已知三次函数$$y=f ~ ( x )$$
A
A.$$\{x | x < 0$$或$$1 < x < 4 \}$$
B.$$\{x | x < 7 \}$$
C.$$\{x | 1 < x < 4 \}$$
D.$$\{x | x > 4$$或$$0 < x < 1 \}$$
3、['一次函数模型的应用'， '二次函数模型的应用'， '对数型函数模型的应用']正确率60.0%有一组试验数据如下表所示;下列所给函数模型较适合的是$${{(}{)}}$$
C
A.$$y=\operatorname{l o g}_{a} x ( a > 1 )$$
B.$$y=a x+b ( a > 1 )$$
C.$$y=a x^{2}+b ( a > 0 )$$
D.$$y=\operatorname{l o g}_{a} x+b ( a > 1 )$$
4、['数列的递推公式'， '二次函数模型的应用'， '等比数列的通项公式'， '等比数列的定义与证明']正确率60.0%已知数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和为$${{S}_{n}}$$，若$$S_{n}=1 6-a_{n}$$，则$$a_{1} a_{2} \dots a_{n}$$的最大的值（）
C
A.$${{3}{2}}$$
B.$${{1}{2}{8}}$$
C.$${{6}{4}}$$
D.$${{6}{3}}$$
5、['二次函数模型的应用'， '函数求值域'， '函数单调性的应用'， '二次函数的图象分析与判断']正确率60.0%函数$$y=x^{2}+x (-1 \leqslant x \leqslant2 )$$的值域是$${{(}{)}}$$
B
A.$$[ 0， 6 ]$$
B.$$[-\frac{1} {4}， 6 ]$$
C.$$[-\frac{1} {2}， 6 ]$$
D.$$[ \frac{3} {4}， 6 ]$$
6、['二次函数模型的应用'， '充分、必要条件的判定'， '函数零点所在区间的判定']正确率40.0%设函数$$f ( x )=a x^{2}+b x+c ( a， b， c \in R$$且$${{a}{>}{0}{)}}$$，则$$` ` f ( f (-\frac b {2 a} ) ) < 0 "$$是$$^\omega f ( x )$$与$$f ( f ( x ) )$$都恰有两个零点$${{”}}$$的$${{(}{)}}$$
C
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
7、['函数的最大(小)值'， '二次函数模型的应用']正确率40.0%函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=~ x \left( \begin{matrix} {| x |-2} \\ \end{matrix} \right)$$在$$[ m， ~ n ]$$上的最小值为$${{−}{1}}$$，最大值为$${{1}}$$，则$${{n}{−}{m}}$$的最大值为（）
A
A.$${{2}{+}{2}{\sqrt {2}}}$$
B.$${\sqrt {2}}$$
C.$${{2}}$$
D.$${{3}{+}{\sqrt {2}}}$$
8、['二次函数模型的应用'， '函数的最大(小)值']正确率60.0%把长为$${{1}{2}{{c}{m}}}$$的细铁丝截成两段，各自围成一个正三角形，那么这两个正三角形面积之和的最小值是
（）
D
A.$$\frac{\sqrt3} {2} \mathrm{\ c m^{2}}$$
B.$${{4}{c}{{m}^{2}}}$$
C.$${{3}{\sqrt {2}}{{c}{m}^{2}}}$$
D.$${{2}{\sqrt {3}}{{c}{m}^{2}}}$$
9、['二次函数模型的应用'， '常见函数的零点'， '利用导数解决函数零点问题'， '函数零点的概念']正确率19.999999999999996%函数$$f \left( x \right)=x e^{x}$$，要使函数$$g \left( x \right)=k \left[ f \left( x \right) \right]^{2}-f \left( x \right)+1$$的零点个数最多，则$${{k}}$$的取值范围为（）
C
A.$${{k}{>}{−}{{e}^{2}}}$$
B.$$k >-e^{2}-e$$
C.$$k <-e^{2}-e$$
D.$${{k}{<}{−}{{e}^{2}}}$$
10、['二次函数模型的应用']正确率60.0%将进货单价为$${{8}{0}}$$元的商品按$${{9}{0}}$$元一个出售时，能卖出$${{4}{0}{0}}$$个，已知这种商品每涨价$${{1}}$$元，其销售量
就要减少$${{2}{0}}$$个，为了获得最大利润，每个售价应定为（）
C
A.$${{8}{5}}$$元
B.$${{9}{0}}$$元
C.$${{9}{5}}$$元
D.$${{1}{0}{0}}$$元
1. 首先确定函数 $$y=2x^2 - mx +1$$ 在区间内存在零点的条件。计算判别式 $$\Delta = m^2 -8 \geq 0$$，解得 $$m \leq -2\sqrt{2}$$ 或 $$m \geq 2\sqrt{2}$$。题目中给出的条件 $$m \geq 4$$ 是 $$m \geq 2\sqrt{2}$$ 的一个子集，因此是充分但不必要条件。答案为 A。
2. 观察三次函数图像，$$f(x)$$ 在 $$x=0$$、$$x=1$$ 和 $$x=4$$ 处有极值点。题目要求 $$f(x)$$ 的单调递增区间，根据图像变化趋势，函数在 $$(-\infty,0)$$ 和 $$(1,4)$$ 上递增。答案为 A。
3. 试验数据随 $$x$$ 增大而增长，但增速逐渐放缓。对数函数 $$y=\log_a x +b$$ 符合这种趋势，而线性或二次函数增长过快或不符合增速变化。答案为 D。
4. 根据递推关系 $$S_n=16-a_n$$，可得 $$a_{n+1}=\frac{1}{2}a_n$$，且 $$a_1=8$$。数列为等比数列，前 $$n$$ 项积为 $$8^n \cdot 2^{-\frac{n(n-1)}{2}}$$。计算得 $$n=4$$ 时积最大为 64。答案为 C。
5. 函数 $$y=x^2+x$$ 在 $$[-1,2]$$ 上的极值点为 $$x=-\frac{1}{2}$$，最小值为 $$-\frac{1}{4}$$；端点 $$x=2$$ 时取得最大值 6。值域为 $$\left[-\frac{1}{4},6\right]$$。答案为 B。
6. 分析 $$f(x)$$ 与 $$f(f(x))$$ 的零点条件，需保证 $$f\left(-\frac{b}{2a}\right)$$ 位于 $$f(x)$$ 的两个零点之间。此时 $$f\left(f\left(-\frac{b}{2a}\right)\right) <0$$ 是充要条件。答案为 C。
7. 函数 $$f(x)=x(|x|-2)$$ 在 $$x=\pm\sqrt{2}$$ 处取得极值 $$\pm1$$。为使区间 $$[m,n]$$ 包含最小值和最大值，最大宽度为 $$2+2\sqrt{2}$$（从 $$-1$$ 到 $$1+\sqrt{2}$$）。答案为 A。
8. 设两段长度分别为 $$x$$ 和 $$12-x$$，正三角形面积和为 $$\frac{\sqrt{3}}{36}(x^2+(12-x)^2)$$。求导得 $$x=6$$ 时和最小，最小值为 $$2\sqrt{3}\,\text{cm}^2$$。答案为 D。
9. 函数 $$g(x)=k(f(x))^2 -f(x)+1$$ 的零点最多需判别式 $$\Delta=1-4k \geq 0$$ 且 $$k \neq 0$$。结合 $$f(x)$$ 的值域分析，当 $$k < -e^2$$ 时零点最多。答案为 D。
10. 设售价为 $$90+x$$ 元，利润 $$P=(10+x)(400-20x)$$。求导得 $$x=5$$ 时利润最大，即售价 95 元。答案为 C。