.jpg)
正确率60.0%一个等腰三角形的周长为$${{2}{0}{，}}$$则底边长$${{y}}$$关于其中一腰长$${{x}}$$的函数关系为（）
D
A.$$y=1 0-x ( 0 < x \leqslant1 0 )$$
B.$$y=1 0-x ( 0 < x < 1 0 )$$
C.$$y=2 0-2 x ( 5 \leq x \leq1 0 )$$
D.$$y=2 0-2 x ( 5 < x < 1 0 )$$
2、['一次函数模型的应用']正确率80.0%防疫部门对某地区乙型流感爆发趋势进行研究发现，从确诊第一名患者开始累计时间$${{t}{(}}$$单位：天$${{)}}$$与病情爆发系数$${{f}{(}{t}{)}}$$之间，满足函数模型：$$f ( t )=\frac{1} {1+e^{-0. 2 2 ( t-2 0 )}}$$，当$$f ( t )=\frac{1} {1 0}$$时，标志着流感疫情将要局部爆发，则此时$${{t}}$$约为$${{(}{)}{(}}$$参考数据：$$\operatorname{l n} 9 \approx2. 2 )$$
A
A.$${{1}{0}}$$
B.$${{2}{0}}$$
C.$${{3}{0}}$$
D.$${{4}{0}}$$
3、['一次函数模型的应用']正确率80.0%牛顿冷却定律，即温度高于周围环境的物体向周围媒质传递热量逐渐冷却时所遵循的规律．如果物体的初始温度为$${{T}_{0}}$$，则经过一定时间$${{t}}$$分钟后的温度$${{T}}$$满足$$T-T_{c}=( \frac{1} {2} )^{\frac{t} {h}} ( T_{0}-T_{c} )$$，其中$${{T}_{c}}$$是环境温度，$${{h}}$$为常数．现有一个$${{1}{0}{5}{℃}}$$的物体，放在室温$${{1}{5}{℃}}$$的环境中，该物体温度降至$${{7}{5}{°}{C}}$$大约用时$${{1}}$$分钟，那么再经过$${{m}}$$分钟后，该物体的温度降至$${{3}{0}{℃}}$$，则$${{m}}$$的值约为$${{(}{)}{(}}$$参考数据：$$\operatorname{l g} 2 \approx0. 3 0 1 0$$，$$\operatorname{l g} 3 \approx0. 4 7 7 1. )$$
B
A.$${{2}{.}{9}}$$
B.$${{3}{.}{4}}$$
C.$${{3}{.}{9}}$$
D.$${{4}{.}{4}}$$
4、['一次函数模型的应用'， '函数单调性的应用']正确率60.0%已知$$f ( x ) \!=\! ( a-3 ) x \!+\! 4 a，$$，对任意$$x_{1} \! \not=\! x_{2}$$都有$$\frac{f \left( x_{1} \right)-f \left( x_{2} \right)} {x_{1}-x_{2}} < 0$$成立，则$${_{a}}$$的取值是$${{(}{)}}$$
D
A.$$( 0， 3 )$$
B.$$( 1， 3 ]$$
C.$$\left( 0， \frac{1} {4} \right]$$
D.$$(-\infty， 3 )$$
5、['一次函数模型的应用'， '对数型函数模型的应用']正确率40.0%中国的$${{5}{G}}$$技术领先世界，$${{5}{G}}$$技术的数学原理之一便是著名的香农公式：$$C=\mathrm{W l o} g_{2} ( 1+\frac{S} {N} ).$$它表示：在受噪声干扰的信道中，最大信息传递速度$${{C}}$$取决于信道带宽$${{W}}$$，信道内信号的平均功率$${{S}}$$，信道内部的高斯噪声功率$${{N}}$$的大小，其中$$\frac{S} {N}$$叫做信噪比．当信噪比较大时，公式中真数中的$${{1}}$$可以忽略不计．按照香农公式，若不改变带宽$${{W}}$$，而将信噪比$$\frac{S} {N}$$从$${{1}{0}{0}{0}}$$提升至$${{8}{0}{0}{0}}$$，则$${{C}}$$大约增加了$$( \ ) ( \operatorname{l g} 2 \approx0. 3 0 1 0 )$$
B
A.$${{1}{0}{％}}$$
B.$${{3}{0}{％}}$$
C.$${{6}{0}{％}}$$
D.$${{9}{0}{％}}$$
6、['一次函数模型的应用'， '对数型函数模型的应用']正确率80.0%$${{2}{0}{2}{0}}$$年$${{1}{1}}$$月$${{2}{4}}$$日凌晨$${{4}}$$时$${{3}{0}}$$分，中国文昌航天发射场又一次“重量级”发射举世瞩目$${{.}}$$长征五号遥五运载火箭点火升空，托举嫦娥五号探测器至地月转移轨道，开启我国首次地外天体采样返回之旅$${{.}}$$已知火箭的最大速度$${{v}{(}}$$单位：$$k m / s )$$和燃料质量$${{M}{(}}$$单位：$${{k}{g}{)}}$$、火箭质量$${{m}{(}}$$单位：$${{k}{g}{)}}$$的关系是$$v=2 \ 0 0 0 \operatorname{l n} \Bigl( 1+\frac M m \Bigr).$$若火箭的最大速度为$$9 \， 2 4 0 \， k m / s$$，则$$\frac{M} {m} \approx($$参考数值：$$e^{4. 6 2} \approx1 0 1 ) ( \mathrm{\qquad} )$$
D
A.$$\frac{1} {1 0 0}$$
B.$$\frac{1} {1 0}$$
C.$${{1}{0}}$$
D.$${{1}{0}{0}}$$
7、['一次函数模型的应用'， '对数型函数模型的应用']正确率80.0%
北京时间$${{2}{0}{2}{1}}$$年$${{1}{0}}$$月$${{1}{6}}$$日$${{0}}$$时$${{2}{3}}$$分，搭载神州十三号载人飞船的长征二号$${{F}}$$遥十三运载火箭，在酒泉卫星发射中心按照预定时间精准点火发射，约$${{5}{8}{2}}$$秒后，神州十三号载人飞船与火箭成功分离，进入预定轨道，顺利将翟志刚、王亚平、叶光富$${{3}}$$名航天员送入太空，发射取得圆满成功．据测算：在不考虑空气阻力的条件下，火箭的最大速度$${{v}{(}}$$单位：$${{m}{/}{s}{)}}$$和燃料的质量$${{M}{(}}$$单位：$${{k}{g}{)}}$$、火箭的质量$${{(}}$$除燃料外$${{)}{m}{(}}$$单位：$${{k}{g}{)}}$$的函数关系是$$\nu=2 0 0 0 \operatorname{l n} ( 1+\frac M m ).$$当火箭的最大速度达到$$1 1. 5 k m / s$$时，则燃料质量与火箭质量之比约为$${{(}{)}{(}}$$参考数据：$$e^{5. 7 5} \approx3 1 4 )$$
B
A.$${{3}{1}{4}}$$
B.$${{3}{1}{3}}$$
C.$${{3}{1}{2}}$$
D.$${{3}{1}{1}}$$
8、['一次函数模型的应用']正确率80.0%$${{2}{0}{2}{0}}$$年$${{1}{1}}$$月$${{2}{4}}$$日凌晨$${{4}}$$时$${{3}{0}}$$分，中国文昌航天发射场，又一次“重量级”发射举世瞩目$${{.}}$$长征五号遥五运载火箭点火升空，托举嫦娥五号探测器至地月转移轨道，开启我国首次地外天体采样返回之旅，已知火箭的最大速度$${{v}{(}}$$单位：$$k m / s )$$和燃料质量$${{M}{(}}$$单位：$${{k}{g}{)}}$$、火箭质量$${{m}{(}}$$单位：$${{k}{g}{)}}$$的关系是$$v=2 0 0 0 \operatorname{l n} ( 1+\frac M m ).$$若火箭的最大速度为$$9 2 4 0 k m / s$$，则$$\frac{M} {m} \approx( \textsubscript{)} ($$参考数值：$$e^{4. 6 2} \approx1 0 1 )$$
D
A.$$\frac{1} {1 0 0}$$
B.$$\frac{1} {1 0}$$
C.$${{1}{0}}$$
D.$${{1}{0}{0}}$$
9、['一次函数模型的应用']正确率80.0%
“喊泉”是一种地下水的毛细现象，人们在泉口吼叫或发出其他声音时，声波传入泉洞内的储水池，进而产生“共鸣”等物理声学作用，激起水波，形或涌泉$${{.}}$$声音超大，涌起的泉水越高$${{.}}$$已知听到的声强$${{m}}$$与标准声强$${{m}_{0}{(}{{m}_{0}}}$$均为$$1 0^{-1 2}$$，单位：$${{W}{/}{{m}^{2}}{)}}$$之比的常用对数称作声强的声强级，记作$${{L}{(}}$$贝尔$${{)}}$$，即$$L=\operatorname{l g} \frac{m} {m_{0}}$$，取贝尔的$${{1}{0}}$$倍作为响度的常用单位，简称为分贝$${{.}}$$已知某处“喊泉”的声音响度$${{y}{(}}$$分贝$${{)}}$$与喷出的泉水高度$${{x}{(}}$$米$${{)}}$$满足关系式$${{y}{=}{2}{x}}$$，现知$${{A}}$$同学大喝一声激起的涌泉最高高度为$${{7}{0}}$$米，若$${{A}}$$同学大喝一声的声强大约相当于$${{1}{0}{0}}$$个$${{B}}$$同学同时大喝一声的声强，则$${{B}}$$同学大喝一声激起的涌泉最高高度约为$${{(}{)}}$$米.
D
A.$${{0}{.}{7}}$$
B.$${{7}}$$
C.$${{5}{0}}$$
D.$${{6}{0}}$$
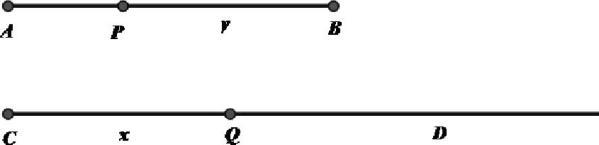
10、['一次函数模型的应用']正确率40.0%如图，假定两点$${{P}}$$，$${{Q}}$$以相同的初速度运动．点$${{Q}}$$沿直线$${{C}{D}}$$作匀速运动，$${{C}{Q}{=}{x}}$$；点$${{P}}$$沿线段$${{A}{B}{(}}$$长度为$${{1}{0}^{7}}$$单位$${{)}}$$运动，它在任何一点的速度值等于它尚未经过的距离$$( P B=y ).$$令$${{P}}$$与$${{Q}}$$同时分别从$${{A}}$$，$${{C}}$$出发，那么，定义$${{x}}$$为$${{y}}$$的纳皮尔对数，用现在的数学符号表示$${{x}}$$与$${{y}}$$的对应关系就是$$y=1 0^{7} ( \frac{1} {e} )^{\frac{x} {1 0^{7}}}$$，其中$${{e}}$$为自然对数的底．当点$${{P}}$$从线段$${{A}{B}}$$的三等分点移动到中点时，经过的时间为$${{(}{)}}$$
D
A.$${{l}{n}{2}}$$
B.$${{l}{n}{3}}$$
C.$$\operatorname{l n} \frac{3} {2}$$
D.$$\operatorname{l n} \frac{4} {3}$$
1. 等腰三角形周长公式为 $$2x + y = 20$$，解得 $$y = 20 - 2x$$。由于三角形两边之和大于第三边，需满足 $$2x > y$$ 即 $$2x > 20 - 2x$$，得 $$x > 5$$；同时 $$y > 0$$ 即 $$20 - 2x > 0$$，得 $$x < 10$$。因此定义域为 $$5 < x < 10$$，正确答案为 D。
2. 根据题意，解方程 $$\frac{1}{1 + e^{-0.22(t - 20)}} = \frac{1}{10}$$，得 $$1 + e^{-0.22(t - 20)} = 10$$，即 $$e^{-0.22(t - 20)} = 9$$。取自然对数得 $$-0.22(t - 20) = \ln 9 \approx 2.2$$，解得 $$t - 20 \approx -10$$，$$t \approx 10$$，正确答案为 A。
3. 根据牛顿冷却定律，代入初始条件 $$75 - 15 = \left(\frac{1}{2}\right)^{\frac{1}{h}}(105 - 15)$$，解得 $$h = \frac{1}{\log_2 \frac{60}{90}} = \frac{1}{\log_2 \frac{2}{3}}$$。再求 $$30 - 15 = \left(\frac{1}{2}\right)^{\frac{1 + m}{h}}(105 - 15)$$，化简得 $$\frac{1}{6} = \left(\frac{2}{3}\right)^{1 + m}$$。取对数解得 $$m \approx 3.4$$，正确答案为 B。
4. 由题意知函数 $$f(x)$$ 单调递减，需满足 $$a - 3 < 0$$ 且 $$f(x)$$ 不增，即 $$a - 3 < 0$$ 且 $$a \leq \frac{1}{4}$$（端点验证）。综合得 $$a \in \left(0, \frac{1}{4}\right]$$，正确答案为 C。
5. 信噪比从 1000 提升至 8000 时，$$C$$ 的变化比为 $$\frac{\log_2 8000 - \log_2 1000}{\log_2 1000} = \frac{\log_2 8}{\log_2 1000} = \frac{3}{10}$$，即增加 30%，正确答案为 B。
6. 由 $$v = 2000 \ln\left(1 + \frac{M}{m}\right)$$ 代入 $$v = 9240$$，得 $$\ln\left(1 + \frac{M}{m}\right) = 4.62$$，即 $$\frac{M}{m} = e^{4.62} - 1 \approx 100$$，正确答案为 D。
7. 同第 6 题模型，代入 $$v = 11.5 \times 1000$$，得 $$\ln\left(1 + \frac{M}{m}\right) = 5.75$$，即 $$\frac{M}{m} = e^{5.75} - 1 \approx 313$$，正确答案为 B。
8. 同第 6 题解析，正确答案为 D。
9. 设 $$B$$ 同学的声强为 $$m_B$$，则 $$A$$ 同学的声强为 $$100m_B$$。由 $$y = 2x$$ 及 $$L = 10 \lg \frac{m}{m_0}$$，得 $$70 = 2 \times 10 \lg \frac{100m_B}{m_0}$$，解得 $$x_B = 60$$ 米，正确答案为 D。
10. 由 $$y = 10^7 \left(\frac{1}{e}\right)^{\frac{x}{10^7}}$$，初始三等分点 $$y = \frac{2}{3} \times 10^7$$ 对应 $$x_1 = 10^7 \ln \frac{3}{2}$$；中点 $$y = \frac{1}{2} \times 10^7$$ 对应 $$x_2 = 10^7 \ln 2$$。时间差为 $$\Delta x = x_2 - x_1 = 10^7 \ln \frac{4}{3}$$，正确答案为 D。