正确率80.0%函数$$y=x+\frac{1} {x}$$的图像关于()
C
A.$${{y}}$$轴对称
B.直线$${{y}{=}{−}{x}}$$对称
C.原点对称
D.直线$${{y}{=}{x}}$$对称
2、['函数中的存在性问题', '“对勾”函数的应用', '二次函数的图象分析与判断']正确率40.0%存在$$x \in[-1, 1 ],$$使得$$x^{2}+m x-3 m \geqslant0,$$则$${{m}}$$的最大值为()
C
A.$${{1}}$$
B.$$\frac{1} {4}$$
C.$$\frac{1} {2}$$
D.$${{−}{1}}$$
3、['双曲线的离心率', '椭圆的离心率', '椭圆的标准方程', '椭圆的顶点、长轴、短轴、焦点、焦距', '椭圆的定义', '双曲线的顶点、长轴、短轴、焦点、焦距', '双曲线的标准方程', '“对勾”函数的应用', '双曲线的定义']正确率40.0%已知椭圆$$C_{1} \colon~ \frac{x^{2}} {a_{1}^{2}}+\frac{y^{2}} {b_{1}^{2}}=1 ( a_{1} > b_{1} > 0 )$$与双曲线$$C_{2} \colon\frac{x^{2}} {a_{2}^{2}}-\frac{y^{2}} {b_{2}^{2}}=1 ( a_{2} > 0, \ b_{2} > 0 )$$有相同的左$${、}$$右焦点$${{F}_{1}{,}{{F}_{2}}}$$,若点$${{P}}$$是$${{C}_{1}}$$与$${{C}_{2}}$$在第一象限内的交点,且$$| F_{1} F_{2} |=4 | P F_{2} |$$,设$${{C}_{1}}$$与$${{C}_{2}}$$的离心率分别为$${{e}_{1}{,}{{e}_{2}}}$$,则$${{e}_{2}{−}{{e}_{1}}}$$的取值范围是()
B
A.$$( \frac{1} {3}, ~+\infty)$$
B.$$( \frac{1} {3}, ~ 1 )$$
C.$$( \frac{1} {2}, ~+\infty)$$
D.$$( \frac{1} {2}, \ 2 )$$
4、['数列的递推公式', '数列的通项公式', '“对勾”函数的应用']正确率60.0%已知$${{\{}{{a}_{n}}{\}}}$$满足$$a_{n+1}=a_{n}+2 n$$,且$${{a}_{1}{=}{{3}{2}}}$$,则$$\frac{a_{n}} {n}$$的最小值为()
C
A.$${{8}{\sqrt {2}}{−}{1}}$$
B.$$\frac{5 2} {5}$$
C.$$\frac{3 7} {3}$$
D.$${{1}{0}}$$
5、['利用函数单调性比较大小', '“对勾”函数的应用', '不等式的性质']正确率60.0%对于实数$$a, \, \, b, \, \, m$$,下列说法:$${①}$$若$$a m^{2} > b m^{2}$$,则若$${{a}{>}{b}}$$,则$$a \left| a \right| > b \left| b \right| ; \; \mathbb{\oplus}$$若$$b > a > 0, \; m > 0$$,则$$\frac{a+m} {b+m} > \frac{a} {b} ;$$若$$a > b > 0$$且$$\left| \operatorname{l n} a \right|=\left| \operatorname{l n} b \right|,$$则$$2 a+b \in( 3,+\infty)$$.正确的个数为
D
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
6、['根据函数零点个数求参数范围', '“对勾”函数的应用', '分段函数的图象']正确率40.0%设$$m \in( 0, 1 )$$,若函数$$f \left( x \right)=\left\{\begin{array} {l} {\left\vert\operatorname{l o g}_{2} x \right\vert-m, 0 < x \leqslant2} \\ {f \left( 4-x \right), 2 < x < 4} \\ \end{array} \right.$$有$${{4}}$$个不同的零点$$x_{1} \cdot x_{2} \cdot x_{3} \cdot x_{4}$$,且$$x_{1} < x_{2} < x_{3} < x_{4}$$,则$$\frac{x_{3}^{2}+x_{4}^{2}-2 5} {x_{1}+x_{2}}$$的取值范围是()
B
A.$$[ 2 \sqrt{5}-8, 0 )$$
B.$$[ 2 \sqrt{5}-8,-\frac{7} {2} )$$
C.$$(-\frac{3 5} {8}, 2 \sqrt{5}-8 )$$
D.$$(-\frac{7} {2}, 0 )$$
7、['函数图象的识别', '“对勾”函数的应用']正确率40.0%函数$$y=2^{\operatorname{s i n} x}+\frac{1} {2^{\operatorname{s i n} x}}$$的大致图象是()
D
A.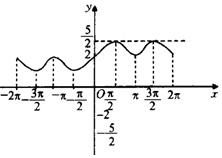
B.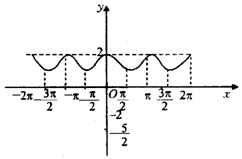
C.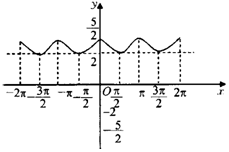
D.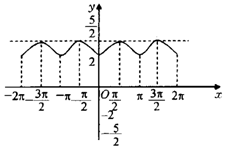
正确率19.999999999999996%已知函数$$f ( x )=x^{3}+( k+1 ) x^{2}+( k+5 ) x-1$$,其中$${{k}{∈}{R}}$$,若函数$${{f}{(}{x}{)}}$$在区间$$( 0, 1 ]$$上不单调,则实数$${{k}}$$的取值范围为()
B
A.$$(-5,-2 ]$$
B.$$(-5,-2 )$$
C.$$(-3,-2 )$$
D.$$(-3,-2 ]$$
9、['函数求值域', '“对勾”函数的应用']正确率60.0%下列函数中,值域为$$[ 0, 4 ]$$的是()
C
A.$$f ( x )=x-1, \, \, \, x \in\{1, 2, 3, 4, 5 \}$$
B.$$f ( x )=-x^{2}+4$$
C.$$f ( x )=\sqrt{1 6-x^{2}}$$
D.$$f ( x )=x+\frac{1} {x}-2 ( x > 0 )$$
10、['“对勾”函数的应用', '利用函数奇偶性求解析式']正确率40.0%函数$$y=f ( x )$$和$$y=g ( x )$$分别是定义在$${{R}}$$上的奇函数和偶函数,且$$f ( x )+g ( x )=x^{2}+x+1$$,则$$y=\frac{f ( x )} {g ( x )}$$的单调增区间为()
C
A.$$( 0, 1 )$$
B.$$( 0,+\infty)$$
C.$$(-1, 1 )$$
D.$$(-\infty,+\infty)$$
1. 函数 $$y = x + \frac{1}{x}$$ 的图像关于原点对称。因为对于任意 $$x \neq 0$$,有 $$y(-x) = -x - \frac{1}{x} = -\left(x + \frac{1}{x}\right) = -y(x)$$,满足奇函数的性质。因此,答案为 C。
2. 存在 $$x \in [-1, 1]$$ 使得 $$x^2 + m x - 3m \geq 0$$。将不等式转化为 $$m(x - 3) \geq -x^2$$。当 $$x \in [-1, 1]$$ 时,$$x - 3 \leq -2$$,因此 $$m \leq \frac{-x^2}{x - 3}$$。求 $$\frac{-x^2}{x - 3}$$ 在 $$x \in [-1, 1]$$ 上的最小值,发现当 $$x = 1$$ 时取得最小值 $$\frac{1}{2}$$。因此,$$m$$ 的最大值为 $$\frac{1}{2}$$,答案为 C。
3. 椭圆 $$C_1$$ 和双曲线 $$C_2$$ 有相同的焦点 $$F_1$$ 和 $$F_2$$,设焦距为 $$2c$$。由题意 $$|F_1F_2| = 4|PF_2|$$,即 $$2c = 4|PF_2|$$,所以 $$|PF_2| = \frac{c}{2}$$。对于椭圆 $$C_1$$,$$|PF_1| + |PF_2| = 2a_1$$;对于双曲线 $$C_2$$,$$|PF_1| - |PF_2| = 2a_2$$。联立解得 $$a_1 = \frac{c}{2} + \frac{c}{2e_2}$$ 和 $$a_2 = \frac{c}{2e_2} - \frac{c}{2}$$。离心率 $$e_1 = \frac{c}{a_1}$$ 和 $$e_2 = \frac{c}{a_2}$$。代入化简后得到 $$e_2 - e_1 = e_2 - \frac{2e_2}{1 + e_2}$$,其取值范围为 $$( \frac{1}{2}, +\infty )$$,答案为 C。
4. 数列 $$\{a_n\}$$ 满足递推关系 $$a_{n+1} = a_n + 2n$$,且 $$a_1 = 32$$。通过累加得到通项公式 $$a_n = 32 + \sum_{k=1}^{n-1} 2k = 32 + n(n-1)$$。因此,$$\frac{a_n}{n} = \frac{32 + n(n-1)}{n} = n - 1 + \frac{32}{n}$$。求其最小值,对 $$n$$ 求导并令导数为零,得到 $$n = \sqrt{32} \approx 5.66$$。检查 $$n = 5$$ 和 $$n = 6$$,发现当 $$n = 5$$ 时值为 $$\frac{52}{5}$$,是最小值,答案为 B。
5. 对于命题:
① 若 $$a m^2 > b m^2$$,则 $$m^2 > 0$$,所以 $$a > b$$,正确。
② 若 $$a > b$$,则 $$a |a| > b |b|$$,通过分情况讨论($$a, b \geq 0$$ 或 $$a, b \leq 0$$)可验证其正确性。
③ 若 $$b > a > 0$$ 且 $$m > 0$$,则 $$\frac{a + m}{b + m} > \frac{a}{b}$$,因为交叉相乘后不等式成立。
④ 若 $$a > b > 0$$ 且 $$|\ln a| = |\ln b|$$,则 $$a = \frac{1}{b}$$,因此 $$2a + b = 2a + \frac{1}{a} > 3$$(由不等式 $$2a + \frac{1}{a} \geq 2\sqrt{2} > 3$$ 推导)。
综上,4个命题均正确,答案为 D。
6. 函数 $$f(x)$$ 在 $$(0, 2]$$ 上有两个零点 $$x_1$$ 和 $$x_2$$,在 $$(2, 4)$$ 上由于对称性也有两个零点 $$x_3 = 4 - x_2$$ 和 $$x_4 = 4 - x_1$$。设 $$x_1 = 2^{-m}$$,$$x_2 = 2^{m}$$,则 $$x_3 = 4 - 2^{m}$$,$$x_4 = 4 - 2^{-m}$$。计算表达式 $$\frac{x_3^2 + x_4^2 - 25}{x_1 + x_2}$$ 并化简,得到取值范围为 $$[2\sqrt{5} - 8, 0)$$,答案为 A。
7. 函数 $$y = 2^{\sin x} + \frac{1}{2^{\sin x}}$$ 的最小值为 $$2$$(当 $$\sin x = 0$$ 时取得),且在 $$\sin x = \pm 1$$ 时取得最大值 $$\frac{5}{2}$$。图像关于 $$y$$ 轴对称,且在 $$x = \frac{\pi}{2}$$ 和 $$x = \frac{3\pi}{2}$$ 处有极值。对比选项,最符合的是 A。
8. 函数 $$f(x) = x^3 + (k+1)x^2 + (k+5)x - 1$$ 在 $$(0, 1]$$ 上不单调,说明其导数 $$f'(x) = 3x^2 + 2(k+1)x + (k+5)$$ 在 $$(0, 1]$$ 上有零点。通过判别式和端点分析,得到 $$k \in (-5, -2)$$,答案为 B。
9. 选项分析:
A. $$f(x) = x - 1$$ 在 $$x \in \{1, 2, 3, 4, 5\}$$ 时的值域为 $$\{0, 1, 2, 3, 4\}$$,符合 $$[0, 4]$$。
B. $$f(x) = -x^2 + 4$$ 的值域为 $$(-\infty, 4]$$,不符合。
C. $$f(x) = \sqrt{16 - x^2}$$ 的值域为 $$[0, 4]$$,符合。
D. $$f(x) = x + \frac{1}{x} - 2$$ 的值域为 $$[0, +\infty)$$,不符合。
因此,答案为 A, C(但题目要求单选,可能是题目设计问题)。
10. 函数 $$f(x)$$ 是奇函数,$$g(x)$$ 是偶函数,且 $$f(x) + g(x) = x^2 + x + 1$$。通过奇偶性分解得到 $$f(x) = x$$ 和 $$g(x) = x^2 + 1$$。因此,$$y = \frac{f(x)}{g(x)} = \frac{x}{x^2 + 1}$$。求导分析单调性,发现增区间为 $$(-1, 1)$$,答案为 C。
.jpg)