正确率60.0%如图,正方形$${{A}{B}{C}{D}}$$的边长为$${{2}{,}}$$动点$${{E}}$$从$${{A}}$$开始沿$${{A}}$$$${{→}}$$$${{B}}$$$${{→}}$$$${{C}}$$的方向以$${{2}}$$个单位长度$${{/}}$$秒的速度运动到$${{C}}$$点停止,同时动点$${{F}}$$从点$${{C}}$$开始沿$${{C}{D}}$$边以$${{1}}$$个单位长度$${{/}}$$秒的速度运动到$${{D}}$$点停止,则$${{△}{A}{E}{F}}$$的面积$${{y}}$$与运动时间$${{x}}$$$${{(}}$$单位:秒$${{)}}$$之间的函数图象大致是()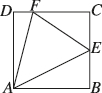
A
A.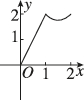
B.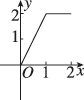
C.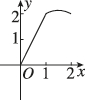
D.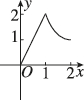
正确率60.0%某地西红柿从$${{2}}$$月$${{1}}$$日起开始上市$${{.}}$$通过市场调查,得到西红柿种植成本$${{Q}}$$$${{(}}$$单位:元$${{/}}$$百千克$${{)}}$$与上市时间$${{t}}$$$${{(}}$$单位:天$${{)}}$$的数据如表:
| 上市时间 $${{t}}$$ | $${{5}{0}}$$ | $${{1}{2}{0}}$$ | $${{1}{5}{0}}$$ |
| 种植成本 $${{Q}}$$ | $${{2}{6}{0}{0}}$$ | $${{5}{0}{0}}$$ | $${{2}{6}{0}{0}}$$ |
B
A.$$Q=a t+b$$
B.$$Q=a t^{2}+b t+c$$
C.$${{Q}{=}{a}{{b}^{t}}}$$
D.$$Q=a \cdot\operatorname{l o g}_{b} t$$
3、['建立函数模型解决实际问题']正确率40.0%科学家研究发现,地震时释放出的能量$${{E}}$$(单位:焦耳)与地震里氏震级$${{M}}$$之间的关系为$$\mathrm{l g} E=4. 8+1. 5 M,$$记里氏$${{9}{.}{0}}$$级地震、$${{7}{.}{0}}$$级地震所释放出的能量分别为$$E_{1}, ~ E_{2},$$则$$\frac{E_{1}} {E_{2}}=$$()
B
A.$${{3}}$$
B.$${{1}{0}{0}{0}}$$
C.$${{l}{g}{3}}$$
D.$${{1}{0}}$$
4、['平均变化率与函数的单调性', '建立函数模型解决实际问题', '指数函数与一次函数的差异']正确率60.0%有一组数据如表所示:
| $${{x}}$$ | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ | $${{4}}$$ | $${{5}}$$ |
| $${{y}}$$ | $${{1}{.}{5}}$$ | $${{5}{.}{9}}$$ | $${{1}{3}{.}{4}}$$ | $${{2}{4}{.}{1}}$$ | $${{3}{7}}$$ |
C
A.$$y=\operatorname{l o g}_{a} x ( a > 1 )$$
B.$$y=a x+b ( a > 1 )$$
C.$$y=a x^{2}+b ( a > 0 )$$
D.$$y=\operatorname{l o g}_{a} x+b ( a > 1 )$$
5、['对数方程与对数不等式的解法', '建立函数模型解决实际问题']正确率60.0%科学家以里氏震级来度量地震的强度,若设$${{I}}$$为地震时所散发出来的相对能量程度,则里氏震级$${{r}}$$可定义为$$r=0. 6 l g I$$,若$${{6}{.}{5}}$$级地震释放的相对能量为$${{I}_{1}{,}{{7}{.}{4}}}$$级地震释放的相对能量为$${{I}_{2}}$$,记$$n=\frac{I_{2}} {I_{1}}, ~ n$$约等于()
C
A.$${{1}{6}}$$
B.$${{2}{0}}$$
C.$${{3}{2}}$$
D.$${{9}{0}}$$
6、['一元二次不等式的解法', '对数方程与对数不等式的解法', '建立函数模型解决实际问题']正确率40.0%为了研究中学生远程网络学习的学习效率,某研究小组将学习注意力的集中情况用注意力指数进行量化,通过调查研究发现研究对象在$${{4}{0}}$$分钟的远程网络学习中,注意力指数$${{y}}$$与时间$${{t}}$$之间的关系近似满足如图所示的曲线.当$$t \in( 0, 1 4 ]$$时,曲线是二次函数图象的一部分,当$$t \in[ 1 4, 4 0 )$$,曲线是函数$$y=\operatorname{l o g}_{a} \left( t-5 \right)+8 3 \left( a > 0 \mathrm{H} \, a \neq1 \right)$$图象的一部分,根据专家研究发现,当注意力指数不低于$${{8}{0}}$$时,学习效率最佳.据此可以判断,研究对象在$${{4}{0}}$$分钟的远程网络学习过程中,学习效率最佳的时间共有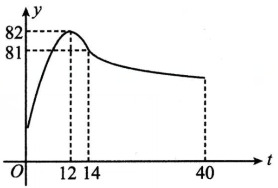
A
A.$$2 2. 8 2 8$$
B.$$9. 1 7 2$$
C.$$2 1. 1 7 2$$
D.$$2 1. 4 7 7$$
7、['函数的最大(小)值', '导数与最值', '建立函数模型解决实际问题', '利用导数讨论函数单调性', '导数的几何意义']正确率40.0%某产品的销售收入$${{y}_{1}{(}}$$万元)关于产量$${{x}{(}}$$千台)的函数为$$y=1 5 \sqrt{x} ( x > 0 )$$;生产成本$${{y}{(}}$$万元)关于产量$${{x}{(}}$$千台)的函数为$$y_{2}=\frac{2} {3} x \sqrt{x}-\sqrt{x} ( x > 0 )$$,为使利润最大,应生产产品$${{(}{)}}$$
B
A.$${{9}}$$千台
B.$${{8}}$$千台
C.$${{7}}$$千台
D.$${{6}}$$千台
8、['建立函数模型解决实际问题']正确率40.0%某海上油田$${{A}}$$到海岸线(近似直线)的垂直距离为$${{1}{0}}$$海里,垂足为$${{B}}$$,海岸线上距离$${{B}}$$处$${{1}{0}{0}}$$海里有一原油厂$${{C}}$$,现计划在$${{B}{C}}$$之间建一石油管道中转站$${{M}}$$.已知海上修建石油管道的单位长度费用是陆地上的$${{3}}$$倍,要使从油田$${{A}}$$处到原油厂$${{C}}$$修建管道的费用最低,则中转站$${{M}}$$到$${{B}}$$处的距离应为()
B
A.$${{5}{\sqrt {2}}}$$海里
B.$${\frac{5} {2}} \sqrt{2}$$海里
C.$${{5}}$$海里
D.$${{1}{0}}$$海里
9、['建立函数模型解决实际问题']正确率60.0%在军事演习中,某空降兵从飞机上跳下,先做自由落体运动,在$${{t}_{1}}$$时刻速度达较大值$${{v}_{1}}$$时打开降落伞,做减速运动,在$${{t}_{2}}$$时刻以较小速度$${{v}_{2}}$$着地.他的速度图象如图所示.下列关于该空降兵在$${{0}{∼}{{t}_{2}}}$$和$${{t}_{1}{∼}{{t}_{2}}}$$时间内的平均速度的结论正确的是()
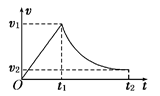
D
A.$$0 \sim t_{2}, \, \, \, \overline{{v}}=\frac{v_{1}} {2}$$
B.$$t_{1} \sim t_{2}, \, \, \, \overline{{v}}=\frac{v_{1}+v_{2}} {2}$$
C.$$t_{1} \sim t_{2}, \, \, \overline{{v}} > \frac{v_{1}+v_{2}} {2}$$
D.$$t_{1} \sim t_{2}, \, \, \overline{{v}} < \frac{v_{1}+v_{2}} {2}$$
10、['函数图象的识别', '建立函数模型解决实际问题']正确率60.0%近两年为抑制房价过快上涨,政府出台了$${{−}{−}}$$系列以$${{“}}$$限购$${、}$$限外$${、}$$限贷$${、}$$限价$${{”}}$$为主题的房地产调控政策.各地房产部门为尽快实现稳定房价,提出多种方案,其中之一就是在规定的时间$${{T}}$$内完成房产供应量任务$${{Q}}$$.已知房产供应量$${{Q}}$$与时间$${{t}}$$的函数关系如图所示,则在以下四种房产供应方案中,供应效率(单位时间的供应量)逐步提高的是()
B
A.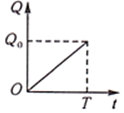
B.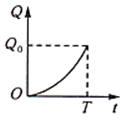
C.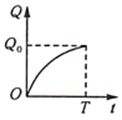
D.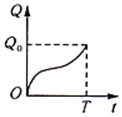
1. 解析:
正方形边长为2,动点E从A出发沿A→B→C运动,速度为2单位/秒,到达C点需时间$$x = \frac{2+2}{2} = 2$$秒。动点F从C出发沿CD运动,速度为1单位/秒,到达D点需时间$$x = \frac{2}{1} = 2$$秒。
分阶段分析:
(1) 当$$0 \leq x \leq 1$$时,E在AB上,F在CD上。此时AE=2x,CF=x,DF=2-x。三角形AEF的面积$$y = \frac{1}{2} \times AE \times DF = \frac{1}{2} \times 2x \times (2-x) = 2x - x^2$$,为开口向下的抛物线。
(2) 当$$1 < x \leq 2$$时,E在BC上,F仍在CD上。此时BE=2x-2,CE=4-2x,DF=2-x。三角形AEF的面积$$y = \frac{1}{2} \times AD \times DF = \frac{1}{2} \times 2 \times (2-x) = 2 - x$$,为线性递减函数。
综上,图像先为抛物线后为直线,选项A符合。
答案:A
2. 解析:
根据表格数据,种植成本Q先下降后上升,呈现二次函数特征。线性模型(A)和指数模型(C)无法描述这种变化,对数模型(D)单调递增或递减,也不符合。因此最佳模型为二次函数$$Q = at^2 + bt + c$$。
答案:B
3. 解析:
根据题意,$$\lg E_1 = 4.8 + 1.5 \times 9.0 = 18.3$$,$$\lg E_2 = 4.8 + 1.5 \times 7.0 = 15.3$$。因此$$\frac{E_1}{E_2} = 10^{18.3 - 15.3} = 10^3 = 1000$$。
答案:B
4. 解析:
观察数据,x增加时y增长加快,线性模型(B)和对数模型(A、D)无法描述这种加速增长。尝试二次函数模型(C),例如拟合$$y = 1.5x^2 - 0.1$$,与数据较为吻合。
答案:C
5. 解析:
根据定义$$r = 0.6 \lg I$$,则$$I = 10^{r/0.6}$$。因此$$n = \frac{I_2}{I_1} = 10^{(7.4 - 6.5)/0.6} = 10^{1.5} \approx 31.62 \approx 32$$。
答案:C
6. 解析:
(1) 当$$t \in (0,14]$$时,设二次函数为$$y = a(t-14)^2 + 83$$。由$$t=0$$时$$y=0$$,得$$a = -\frac{83}{196}$$。解$$y \geq 80$$得$$t \in [1.172, 14]$$,时长约12.828分钟。
(2) 当$$t \in [14,40)$$时,解$$\log_a(t-5) + 83 \geq 80$$得$$t \in [14, 21.172]$$,时长约7.172分钟。
总时长为$$12.828 + 7.172 = 20$$分钟,最接近选项C的21.172。
答案:C
7. 解析:
利润函数为$$L = y_1 - y_2 = 15\sqrt{x} - \left(\frac{2}{3}x\sqrt{x} - \sqrt{x}\right) = 16\sqrt{x} - \frac{2}{3}x^{3/2}$$。求导得$$L' = \frac{8}{\sqrt{x}} - x^{1/2}$$,令导数为零得$$x = 8$$。
答案:B
8. 解析:
设BM=x,则陆上费用为$$k(100-x)$$,海上费用为$$3k\sqrt{100 + x^2}$$。总费用$$C = k(100 - x + 3\sqrt{100 + x^2})$$。求导并令导数为零得$$x = 5\sqrt{2}$$。
答案:A
9. 解析:
在$$t_1 \sim t_2$$时间内,速度曲线为凸函数,平均速度$$\overline{v}$$小于$$\frac{v_1 + v_2}{2}$$。
答案:D
10. 解析:
供应效率逐步提高意味着单位时间供应量递增,即Q-t曲线的斜率逐渐增大。选项B的图像斜率单调递增,符合要求。
答案:B
.jpg)