正确率60.0%山顶到山下的招待所的距离为$${{2}{0}}$$千米,某人从山顶以$${{4}}$$千米/小时的速度到山下的招待所,他与招待所间的距离$${{s}}$$(千米)与时间$${{t}}$$(小时)的函数关系用图象表示为()
C
A.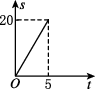
B.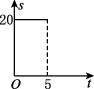
C.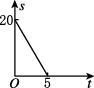
D.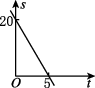
我们需要确定距离$$s$$与时间$$t$$的函数关系,并选择正确的图象。
1. **初始条件**:
- 山顶到山下的招待所的距离为$$20$$千米。
- 人以$$4$$千米/小时的速度从山顶出发走向招待所。
- 初始时刻$$t=0$$时,人与招待所的距离$$s=20$$千米。
2. **函数关系推导**:
- 速度$$v=4$$千米/小时,表示每小时距离减少$$4$$千米。
- 因此,距离与时间的关系为线性函数:$$s = 20 - 4t$$。
- 当人到达招待所时,$$s=0$$,解得$$t=5$$小时。
- 时间$$t$$的取值范围为$$0 \leq t \leq 5$$。
3. **图象分析**:
- 图象应为一条从$$(0,20)$$到$$(5,0)$$的直线,斜率为$$-4$$。
- 选项A:直线从$$(0,20)$$到$$(5,0)$$,符合函数关系。
- 选项B:直线从$$(0,0)$$到$$(5,20)$$,不符合。
- 选项C:曲线,不符合线性关系。
- 选项D:直线从$$(0,0)$$到$$(5,20)$$,不符合。
4. **结论**:
- 正确的图象是选项A。
最终答案是:$$A$$。
题目来源于各渠道收集,若侵权请联系下方邮箱.jpg)