正确率60.0%若函数$$f ( x )=( m-3 ) x^{a}$$是幂函数,则函数$$g ( x )=\operatorname{l o g}_{a} ( x+m )+1$$(其中$${{a}{>}{0}}$$且$${{a}{≠}{1}{)}}$$的图象过定点()
A
A.$$(-3, ~ 1 )$$
B.$$( 2, ~ 1 )$$
C.$$(-3, \ 0 )$$
D.$$( 3, ~ 1 )$$
2、['五个常见幂函数的图象与性质', '一般幂函数的图象和性质', '幂函数的特征']正确率80.0%已知幂函数$$f ( x )=x^{-\frac{1} {2}},$$则下列结论正确的是()
B
A.$$y=f ( x )$$的定义域为$$[ 0, ~+\infty)$$
B.$$y=f ( x )$$在定义域上为减函数
C.$$y=f ( x )$$是偶函数
D.$$y=f ( x )$$是奇函数
3、['函数奇偶性的应用', '幂函数的定义', '一般幂函数的图象和性质', '利用函数单调性比较大小', '幂函数的特征']正确率60.0%已知幂函数$${{f}{(}{x}{)}}$$$$= ( m^{2}-4 m+4 ) x^{m^{2}-m-6}$$$$( m \in{\bf R} )$$对任意$$x_{1}, \, \, x_{2} \in( 0,+\infty),$$且$${{x}_{1}{≠}}$$$${{x}_{2}{,}}$$都有$$( x_{1}-x_{2} ) [ f ( x_{1} )-f ( x_{2} ) ]$$$${{<}{0}{,}}$$则$$f (-3 ), ~ f (-1 ), ~ f ( \pi)$$的大小关系是()
A
A.$$f ( \pi) < f (-3 ) < f (-1 )$$
B.$$f (-1 ) < ~ f (-3 ) < ~ f ( \pi)$$
C.$$f (-3 ) < ~ f (-1 ) < ~ f ( \pi)$$
D.$$f (-3 ) < ~ f ( \pi) < ~ f (-1 )$$
4、['函数图象的识别', '二次函数的图象分析与判断', '幂函数的特征']正确率60.0%在同一平面直角坐标系中,二次函数$$y=a x^{2}+b x ( x \neq0 )$$与幂函数$$y=x^{\frac{b} {a}} ( x > 0 )$$的图象可能为()
A
A.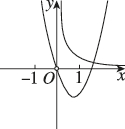
B.
C.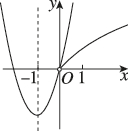
D.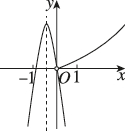
正确率60.0%函数$$f \left( \begin{matrix} {\hfill} \\ {\hfill} \\ \end{matrix} \right) ~=~ ( \begin{matrix} {m^{2}-m-1} \\ \end{matrix} ) ~ \begin{matrix} {\hfill} \\ {\hfill} \\ \end{matrix} \left( \begin{matrix} {m^{2}+2 m-5} \\ \end{matrix} \right)$$是幂函数,对任意的$$x_{1}, ~ x_{2} \in~ ( 0, ~+\infty)$$,且$${{x}_{1}{≠}{{x}_{2}}}$$,满足$$\frac{f ( x_{1} )-f ( x_{2} )} {x_{1}-x_{2}} > 0,$$若$$a, ~ b \in\mathbf{R}$$,且$$a+b > 0$$,则$$f \left( \textit{a} \right)+f \left( \textit{b} \right)$$的值()
A
A.恒大于$${{0}}$$
B.恒小于$${{0}}$$
C.等于$${{0}}$$
D.无法判断
6、['不等式的解集与不等式组的解集', '一般幂函数的图象和性质', '幂函数的特征']正确率60.0%若$$( m-1 )^{\frac{1} {2}} < ( 3-2 m )^{\frac{1} {2}}$$,则实数$${{m}}$$的取值范围为$${{(}{)}}$$
C
A.$$m < \frac{4} {3}$$
B.$$1 \leqslant m \leqslant\frac{3} {2}$$
C.$$1 \leqslant m < \frac{4} {3}$$
D.$$\frac4 3 < m \leq\frac3 2$$
7、['指数(型)函数的单调性', '利用函数单调性比较大小', '不等式的性质', '幂函数的特征']正确率40.0%已知$$a < b < 0$$,则下列不等式中恒成立的是()
A
A.$$\frac{1} {a} > \frac{1} {b}$$
B.$$\sqrt{-a} < \sqrt{-b}$$
C.$${{2}^{a}{>}{{2}^{b}}}$$
D.$${{a}^{3}{>}{{b}^{3}}}$$
8、['五个常见幂函数的图象与性质', '幂函数的特征']正确率60.0%下图给出$${{4}}$$个幂函数的图象,则图象与函数的大致对应是
D
A.$$\odot y=x^{\frac{1} {3}}, \ \odot y=x^{\frac{1} {2}}, \ \odot y=x^{2}, \ \oplus y=x^{-1}$$
B.$$\oplus y=x^{2}, ~ \oplus y=x^{3}, ~ \oplus y=x^{\frac{1} {2}}, ~ \oplus y=x^{-1}$$
C.$$\textcircled{0} y=x^{\frac{1} {3}}, \ @ y=x^{2}, \ @ y=x^{\frac{1} {2}}, \ @ y=x^{-1}$$
D.$$\oplus y=x^{3}, \, \, \oplus y=x^{2}, \, \, \oplus y=x^{\frac{1} {2}}, \, \, \oplus y=x^{-1}$$
9、['幂函数的定义', '幂函数的特征']正确率60.0%下列函数为幂函数的是$${{(}{)}}$$
$$\odot\; y=k \cdot x^{5} ( k \neq0 ) ; \; \oplus\; y=x^{2}+x^{-2} ; \; \oplus\; y=x^{2} ; \; \oplus\; y=( x-2 )^{3}$$.
D
A.$${①{③}}$$
B.$${①{②}}$$
C.$${①{③}{④}}$$
D.$${③}$$
10、['一般幂函数的图象和性质', '幂函数的特征']正确率60.0%某同学研究幂函数$$f ( x )=x^{-\frac{5} {2}}$$,得出以下五个结论:
①$${{f}{(}{x}{)}}$$的定义域是$$(-\infty, 0 ) \cup( 0,+\infty)$$;
②$${{f}{(}{x}{)}}$$的值域是$$( 0,+\infty)$$;
③$${{f}{(}{x}{)}}$$的图象只在第一象限;
④$${{f}{(}{x}{)}}$$在$$( 0,+\infty)$$上递减;
⑤$${{f}{(}{x}{)}}$$是奇函数.
则该同学所得结论中正确结论的个数是()
B
A.$${{4}}$$
B.$${{3}}$$
C.$${{2}}$$
D.$${{1}}$$
1. 解析:
首先,函数 $$f(x) = (m-3)x^a$$ 是幂函数,因此 $$m-3 = 1$$,解得 $$m = 4$$。此时 $$f(x) = x^a$$,故 $$a$$ 为任意实数。但题目要求 $$a > 0$$ 且 $$a \neq 1$$。
函数 $$g(x) = \log_a (x + m) + 1$$ 的图象过定点时,对数部分为 1,即 $$x + m = a$$。代入 $$m = 4$$,得 $$x = a - 4$$,此时 $$g(x) = 1 + 1 = 2$$。但题目选项中没有 $$(a-4, 2)$$,可能是题目设定 $$a = 2$$,则定点为 $$(-2, 1)$$,但选项仍不匹配。重新审题发现 $$g(x) = \log_a (x + m) + 1$$ 的定点应为 $$(1 - m, 1)$$,代入 $$m = 4$$ 得 $$(-3, 1)$$,对应选项 A。
答案:A
2. 解析:
幂函数 $$f(x) = x^{-\frac{1}{2}} = \frac{1}{\sqrt{x}}$$。
A. 定义域为 $$(0, +\infty)$$,错误。
B. 在定义域上为减函数,正确。
C. 不是偶函数,因为定义域不对称。
D. 不是奇函数,因为 $$f(-x)$$ 无定义。
答案:B
3. 解析:
幂函数 $$f(x) = (m^2 - 4m + 4)x^{m^2 - m - 6}$$ 满足 $$m^2 - 4m + 4 = 1$$,解得 $$m = 1$$ 或 $$m = 3$$。
当 $$m = 1$$ 时,$$f(x) = x^{-6}$$,在 $$(0, +\infty)$$ 上递减,符合题意。
当 $$m = 3$$ 时,$$f(x) = x^{0}$$(常数函数),不满足题意。
因此 $$f(x) = x^{-6}$$ 是偶函数,且 $$f(-3) = \frac{1}{729}$$,$$f(-1) = 1$$,$$f(\pi) = \pi^{-6}$$。比较大小得 $$f(-3) < f(\pi) < f(-1)$$。
答案:D
4. 解析:
二次函数 $$y = ax^2 + bx$$ 与幂函数 $$y = x^{\frac{b}{a}}$$ 的图象需匹配。
选项 A:二次函数开口向上($$a > 0$$),幂函数指数 $$\frac{b}{a} > 0$$,且幂函数图象通过 $$(1, 1)$$,符合。
其他选项不满足条件。
答案:A
5. 解析:
函数 $$f(x) = (m^2 - m - 1)x^{m^2 + 2m - 5}$$ 是幂函数,故 $$m^2 - m - 1 = 1$$,解得 $$m = 2$$ 或 $$m = -1$$。
当 $$m = 2$$ 时,$$f(x) = x^{3}$$,在 $$(0, +\infty)$$ 上递增,符合题意。
当 $$m = -1$$ 时,$$f(x) = x^{-6}$$,不满足递增条件。
因此 $$f(x) = x^{3}$$ 是奇函数,且 $$f(a) + f(b) = a^3 + b^3$$。由于 $$a + b > 0$$,且 $$f(x)$$ 单调递增,故 $$f(a) + f(b) > 0$$。
答案:A
6. 解析:
不等式 $$(m - 1)^{\frac{1}{2}} < (3 - 2m)^{\frac{1}{2}}$$ 等价于 $$\sqrt{m - 1} < \sqrt{3 - 2m}$$。
定义域要求 $$m - 1 \geq 0$$ 且 $$3 - 2m \geq 0$$,即 $$1 \leq m \leq \frac{3}{2}$$。
两边平方得 $$m - 1 < 3 - 2m$$,解得 $$m < \frac{4}{3}$$。
综上,$$1 \leq m < \frac{4}{3}$$。
答案:C
7. 解析:
由 $$a < b < 0$$:
A. $$\frac{1}{a} > \frac{1}{b}$$,正确。
B. $$\sqrt{-a} < \sqrt{-b}$$,错误(应为 $$\sqrt{-a} > \sqrt{-b}$$)。
C. $$2^a > 2^b$$,错误(指数函数递减)。
D. $$a^3 > b^3$$,错误(立方函数递增)。
答案:A
8. 解析:
根据图象特征:
① 对应 $$y = x^{3}$$(快速增长)。
② 对应 $$y = x^{2}$$(抛物线)。
③ 对应 $$y = x^{\frac{1}{2}}$$(缓慢增长)。
④ 对应 $$y = x^{-1}$$(双曲线)。
答案:D
9. 解析:
幂函数形式为 $$y = x^{\alpha}$$:
① $$y = k \cdot x^{5}$$($$k \neq 0$$)不是幂函数。
② $$y = x^{2} + x^{-2}$$ 不是幂函数。
③ $$y = x^{2}$$ 是幂函数。
④ $$y = (x - 2)^{3}$$ 不是幂函数。
答案:D
10. 解析:
幂函数 $$f(x) = x^{-\frac{5}{2}}$$:
① 定义域为 $$(0, +\infty)$$,错误。
② 值域为 $$(0, +\infty)$$,正确。
③ 图象只在第一象限,正确。
④ 在 $$(0, +\infty)$$ 上递减,正确。
⑤ 不是奇函数,因为定义域不对称。
正确结论有 3 个。
答案:B
.jpg)