.jpg)
正确率60.0%已知幂函数$$f ( x )=( k^{2}-2 k-1 4 ) x^{k}$$在$$( 0， ~+\infty)$$上单调递增，则$${{k}{=}}$$（）
D
A.$${{−}{3}}$$
B.$${{3}}$$
C.$${{−}{5}}$$
D.$${{5}}$$
2、['函数奇偶性的应用'， '函数奇、偶性的证明'， '函数奇、偶性的图象特征'， '函数奇、偶性的定义'， '五个常见幂函数的图象与性质'， '幂函数的定义'， '一般幂函数的图象和性质'， '幂函数的特征']正确率19.999999999999996%若幂函数$$y=( m^{2}-3 m+3 ) x^{m-2}$$的图象不过原点且在定义域上为奇函数，则（）
D
A.$$1 \leqslant m \leqslant2$$
B.$${{m}{=}{1}}$$或$${{m}{=}{2}}$$
C.$${{m}{=}{2}}$$
D.$${{m}{=}{1}}$$
3、['一般幂函数的图象和性质'， '幂函数的特征']正确率60.0%已知函数$$y=x^{m^{2}-5 m+4} \， \， ( \， m \in Z )$$为偶函数且在区间$$( \mathrm{\bf~ 0}， \mathrm{\bf~ \Lambda}+\infty)$$上单调递减，则$${{m}{=}{（}}$$）
A
A.$${{2}}$$或$${{3}}$$
B.$${{3}}$$
C.$${{2}}$$
D.$${{1}}$$
4、['五个常见幂函数的图象与性质'， '利用函数单调性比较大小'， '幂函数的特征']正确率60.0%已知点$$( 2， \ 8 )$$在幂函数$$f ( x )=x^{n}$$的图象上，设$$a=f \left( \frac{\sqrt{3}} {3} \right)， \， \， \， b=f ( \operatorname{l n} \pi)， \， \， \， c=f \left( \frac{\sqrt{2}} {2} \right)，$$则$$a， ~ b， ~ c$$的大小关系为（）
A
A.$$a < c < b$$
B.$$a < b < c$$
C.$$b < c < a$$
D.$$b < a < c$$
5、['不等式的解集与不等式组的解集'， '一般幂函数的图象和性质'， '幂函数的特征']正确率60.0%若$$( m-1 )^{\frac{1} {2}} < ( 3-2 m )^{\frac{1} {2}}$$，则实数$${{m}}$$的取值范围为$${{(}{)}}$$
C
A.$$m < \frac{4} {3}$$
B.$$1 \leqslant m \leqslant\frac{3} {2}$$
C.$$1 \leqslant m < \frac{4} {3}$$
D.$$\frac4 3 < m \leq\frac3 2$$
6、['函数奇、偶性的定义'， '幂函数的定义'， '一般幂函数的图象和性质'， '幂函数的特征']正确率60.0%已知函数$$f ( x )=( 2 n-1 ) x^{-m^{2}+2 m+3}$$，其中$${{m}{∈}{N}}$$，若函数$${{f}{(}{x}{)}}$$为幂函数且其在$$( 0，+\infty)$$上是单调递增的，并且在其定义域上是偶函数，则$$m+n=( \eta)$$
A
A.$${{2}}$$
B.$${{3}}$$
C.$${{4}}$$
D.$${{5}}$$
7、['幂函数的定义'， '幂函数的特征']正确率80.0%已知幂函数$$f ( x )=\lambda\cdot x^{a}$$的图象过点$$( \frac{1} {2}， \frac{\sqrt{2}} {2} )$$，则$${{λ}{+}{α}{=}}$$
B
A.$$\frac{1} {2}$$
B.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
C.$${{1}}$$
D.$${{2}}$$
8、['幂函数的定义'， '幂函数的特征']正确率60.0%幂函数$${{y}{=}{k}{{x}^{a}}}$$过点$$( 4， \ 2 )$$，则$${{k}{−}{a}}$$的值为（）
B
A.$${{−}{1}}$$
B.$$\frac{1} {2}$$
C.$${{1}}$$
D.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
9、['负分数指数幂'， '幂函数的定义'， '幂函数的特征']正确率60.0%已知函数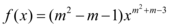
是幂函数，且当 $${{x}}$$$$\in( 0，+\infty)$$时， $${{f}}$$( $${{x}}$$)是减函数，
则 $${{m}}$$的值为$${{(}{)}}$$
A
A.$${{−}{1}}$$
B.$${{2}}$$
C.$${{−}{1}}$$或$${{2}}$$
D.$${{3}}$$
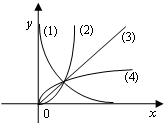
10、['五个常见幂函数的图象与性质'， '幂函数的特征']正确率60.0%已知函数$$( 1 ) y=x^{a}， ( 2 ) y=x^{b}， ( 3 ) y=x^{c}， ( 4 ) y=x^{d}$$，在第一象限内的函数图象如图所示，那么 （）
D
A.$$a > b > c > d$$
B.$$a > d > b > c$$
C.$$c > a > b > d$$
D.$$b > c > d > a$$
1. 解析：
幂函数 $$f(x) = (k^2 - 2k - 14)x^k$$ 在 $$(0, +\infty)$$ 上单调递增，需满足：
1. 系数 $$k^2 - 2k - 14 = 1$$，解得 $$k^2 - 2k - 15 = 0$$，即 $$k = 5$$ 或 $$k = -3$$。
2. 指数 $$k > 0$$，排除 $$k = -3$$，因此 $$k = 5$$。
答案：D。
2. 解析：
幂函数 $$y = (m^2 - 3m + 3)x^{m-2}$$ 满足：
1. 系数 $$m^2 - 3m + 3 \neq 0$$（恒成立，因为判别式 $$9 - 12 < 0$$）。
2. 图象不过原点，需 $$m - 2 < 0$$，即 $$m < 2$$。
3. 为奇函数，需 $$m - 2$$ 为奇数，即 $$m$$ 为奇数。
结合选项，$$m = 1$$ 满足条件。
答案：D。
3. 解析：
函数 $$y = x^{m^2 - 5m + 4}$$ 为偶函数且在 $$(0, +\infty)$$ 上单调递减，需满足：
1. 指数 $$m^2 - 5m + 4$$ 为偶数。
2. 指数 $$m^2 - 5m + 4 < 0$$，解得 $$1 < m < 4$$。
结合 $$m \in \mathbb{Z}$$，$$m = 2$$ 或 $$m = 3$$。
验证：
- 当 $$m = 2$$ 时，指数为 $$-2$$（偶数且小于 0），符合条件。
- 当 $$m = 3$$ 时，指数为 $$-2$$（同上），符合条件。
答案：A。
4. 解析：
点 $$(2, 8)$$ 在幂函数 $$f(x) = x^n$$ 上，代入得 $$2^n = 8$$，解得 $$n = 3$$。
比较 $$a = f\left(\frac{\sqrt{3}}{3}\right)$$，$$b = f(\ln \pi)$$，$$c = f\left(\frac{\sqrt{2}}{2}\right)$$：
由于 $$f(x) = x^3$$ 在 $$(0, +\infty)$$ 上单调递增，且 $$\ln \pi > \frac{\sqrt{2}}{2} > \frac{\sqrt{3}}{3}$$，因此 $$a < c < b$$。
答案：A。
5. 解析：
不等式 $$(m - 1)^{1/2} < (3 - 2m)^{1/2}$$ 成立的条件为：
1. 根号内非负：$$m - 1 \geq 0$$ 且 $$3 - 2m \geq 0$$，即 $$1 \leq m \leq \frac{3}{2}$$。
2. 平方后不等式：$$m - 1 < 3 - 2m$$，解得 $$m < \frac{4}{3}$$。
综上，$$1 \leq m < \frac{4}{3}$$。
答案：C。
6. 解析：
函数 $$f(x) = (2n - 1)x^{-m^2 + 2m + 3}$$ 为幂函数且满足：
1. 系数 $$2n - 1 = 1$$，解得 $$n = 1$$。
2. 在 $$(0, +\infty)$$ 上单调递增，需 $$-m^2 + 2m + 3 > 0$$，即 $$-1 < m < 3$$。
3. 为偶函数，需 $$-m^2 + 2m + 3$$ 为偶数。
结合 $$m \in \mathbb{N}$$，$$m = 1$$ 或 $$m = 2$$。
验证：
- 当 $$m = 1$$ 时，指数为 $$4$$（偶数且大于 0），符合条件。
- 当 $$m = 2$$ 时，指数为 $$3$$（奇数），不符合条件。
因此 $$m = 1$$，$$n = 1$$，$$m + n = 2$$。
答案：A。
7. 解析：
幂函数 $$f(x) = \lambda x^a$$ 过点 $$\left(\frac{1}{2}, \frac{\sqrt{2}}{2}\right)$$，代入得：
$$\lambda \left(\frac{1}{2}\right)^a = \frac{\sqrt{2}}{2}$$。
注意到 $$\frac{\sqrt{2}}{2} = \left(\frac{1}{2}\right)^{1/2}$$，因此 $$\lambda = 1$$，$$a = \frac{1}{2}$$。
故 $$\lambda + a = \frac{3}{2}$$。
答案：B。
8. 解析：
幂函数 $$y = kx^a$$ 过点 $$(4, 2)$$，代入得 $$k \cdot 4^a = 2$$。
注意到 $$4^{1/2} = 2$$，因此 $$k = 1$$，$$a = \frac{1}{2}$$。
故 $$k - a = \frac{1}{2}$$。
答案：B。
9. 解析：
函数 $$f(x) = (m^2 - m - 1)x^{m^2 - 2m - 1}$$ 为幂函数且满足：
1. 系数 $$m^2 - m - 1 = 1$$，解得 $$m^2 - m - 2 = 0$$，即 $$m = 2$$ 或 $$m = -1$$。
2. 在 $$(0, +\infty)$$ 上为减函数，需 $$m^2 - 2m - 1 < 0$$。
验证：
- 当 $$m = 2$$ 时，指数为 $$-1$$（小于 0），符合条件。
- 当 $$m = -1$$ 时，指数为 $$2$$（大于 0），不符合条件。
因此 $$m = 2$$。
答案：B。
10. 解析：
根据幂函数图象在第一象限的性质：
- 指数越大，增长越快，因此 $$a > d > b > c$$。
答案：B。