正确率60.0%设$$a \in\left\{1, \frac{2} {3}, 3,-\frac{1} {3} \right\}$$,则使函数$${{y}{=}{{x}^{a}}}$$的定义域为$${{R}}$$,且为奇函数的$${{a}}$$的所有取值为()
A
A.$${{1}{,}{3}}$$
B.$$1, ~ 3, ~-\frac{1} {3}$$
C.$$1, ~ 3, ~ \frac{2} {3}$$
D.$$1, ~ \frac{2} {3}, ~ 3, ~-\frac{1} {3}$$
2、['利用函数单调性解不等式', '一般幂函数的图象和性质']正确率60.0%若$$( 2 m+1 )^{-\frac{3} {2}} < ( m^{2}+m-1 )^{-\frac{3} {2}}.$$则实数$${{m}}$$的取值范围是()
D
A.$$\left(-\infty, \frac{-\sqrt{5}-1} {2} \right)$$
B.$$\left( \frac{\sqrt{5}-1} {2},+\infty\right)$$
C.$$(-1, 2 )$$
D.$$\left( \frac{\sqrt{5}-1} {2}, 2 \right)$$
3、['实数指数幂的运算性质', '一般幂函数的图象和性质']正确率60.0%幂函数$$y=x^{\alpha} ( \alpha\neq0 ),$$当$${{α}}$$取不同的正数时,在区间$$[ 0, 1 ]$$上它们的图像是一簇曲线(如图).设点$$A ( 1, 0 ), ~ B ( 0, 1 ),$$连接$${{A}{B}{,}}$$线段$${{A}{B}}$$恰好被其中的两个幂函数$$y=x^{m}, ~ y=x^{n}$$的图像三等分,即$$B M=M N=N A ( M, N )$$分别为曲线$$y=x^{m}, y=x^{n}$$与$${{A}{B}}$$的交点),则$${{m}{n}}$$等于()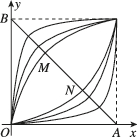
A
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.无法确定
4、['幂函数的定义', '一般幂函数的图象和性质']正确率60.0%已知幂函数$$y=( a^{2}-2 a-2 ) x^{a}$$在实数集$${{R}}$$上单调,那么实数$${{a}}$$等于()
B
A.$${{−}{1}}$$或$${{3}}$$
B.$${{3}}$$
C.$${{−}{3}}$$
D.$${{1}}$$
5、['函数求值域', '函数单调性的判断', '一般幂函数的图象和性质']正确率60.0%下列函数中,值域为$${{R}}$$且在区间$$( 0,+\infty)$$上单调递增的是 ( )
B
A.$$y=-2 x^{3}$$
B.$$y=x | x |$$
C.$$y=x^{-1}$$
D.$${{y}{=}{\sqrt {x}}}$$
6、['一般幂函数的图象和性质']正确率60.0%设$$f \left( x \right)=x^{\alpha}, \alpha\in\{-1, \frac{1} {2}, 1, 2, 3 \}$$,若$${{f}{{(}{x}{)}}}$$的定义域为$${{R}}$$且为偶函数$${{a}}$$的值为()
B
A.$${{1}{,}{3}}$$
B.$${{2}}$$
C.$$\frac{1} {2}, 2$$
D.$$- 1, ~ 1, ~ 3$$
7、['命题的真假性判断', '一般幂函数的图象和性质', '幂函数的特征']正确率60.0%下列结论中,正确的是()
C
A.幂函数的图象都通过点$$( \ 0, \ 0 ) \, \quad( \ 1, \ 1 )$$
B.幂函数的图象可以出现在第四象限
C.当幂指数$${{α}}$$取$$1, ~ 3, ~ \frac{1} {2}$$时,幂函数$${{y}{=}{{x}^{a}}}$$在定义域上是增函数
D.当幂指数$${{α}{=}{−}{1}}$$时,幂函数$${{y}{=}{{x}^{a}}}$$在定义域上是减函数
8、['函数奇偶性的应用', '函数单调性的判断', '幂函数的定义', '一般幂函数的图象和性质', '利用函数单调性比较大小']正确率40.0%已知函数$$f ( x )=( m^{2}-m-1 ) x^{m^{2}+m-1}$$是幂函数,对任意的$$x_{1}, x_{2} \in( 0,+\infty)$$,且$$x_{1} \neq x_{2}, ( x_{1}-x_{2} ) [ f ( x_{1} )-f ( x_{2} ) ] > 0,$$,若$$a, b \in R$$且$$a+b > 0, a b < 0$$,则$$f ( a )+f ( b )$$的值()
B
A.恒小于$${{0}}$$
B.恒大于$${{0}}$$
C.等于$${{0}}$$
D.无法判断
9、['指数(型)函数的单调性', '利用函数单调性比较大小', '一般幂函数的图象和性质']正确率60.0%已知$$a=2^{0. 4}, \, \, \, b=9^{0. 2}, \, \, \, c=\, \, ( \sqrt{3} )^{\, \, \, 3}$$,则()
A
A.$$a < b < c$$
B.$$a < c < b$$
C.$$c < a < b$$
D.$$c < b < a$$
10、['利用函数单调性求参数的取值范围', '幂函数的定义', '一般幂函数的图象和性质']正确率60.0%已知幂函数$$f ( x )=( m^{2}-m-5 ) x^{2 m+3}$$在$$( 0,+\infty)$$上为增函数,则$${{m}}$$值为$${{(}{)}}$$
A
A.$${{3}}$$
B.$${{4}}$$
C.$${{−}{2}}$$
D.$${{−}{2}}$$或$${{3}}$$
1. 解析:函数 $$y = x^a$$ 的定义域为 $$R$$ 且为奇函数,需满足:
2. 解析:不等式 $$(2m+1)^{-3/2} < (m^2 + m - 1)^{-3/2}$$ 可转化为:
3. 解析:线段 $$AB$$ 的方程为 $$y = -x + 1$$。三等分点为 $$M\left(\frac{2}{3}, \frac{1}{3}\right)$$ 和 $$N\left(\frac{1}{3}, \frac{2}{3}\right)$$。
4. 解析:幂函数 $$y = (a^2 - 2a - 2)x^a$$ 在 $$R$$ 上单调,需满足:
5. 解析:
6. 解析:函数 $$f(x) = x^\alpha$$ 为偶函数且定义域为 $$R$$,需 $$\alpha$$ 为偶数或特定形式(如 $$\alpha = 2$$)。选项中仅 $$\alpha = 2$$ 满足。答案为 B。
7. 解析:
8. 解析:由幂函数定义得 $$m^2 - m - 1 = 1$$,解得 $$m = 2$$ 或 $$m = -1$$。由单调递增性知 $$m = 2$$,此时 $$f(x) = x^5$$ 为奇函数。
9. 解析:计算得 $$a = 2^{0.4} \approx 1.32$$,$$b = 9^{0.2} = 3^{0.4} \approx 1.55$$,$$c = (\sqrt{3})^3 \approx 5.20$$。但实际 $$c = 3^{1.5} \approx 5.20$$,显然 $$a < b < c$$。答案为 A。
10. 解析:幂函数 $$f(x) = (m^2 - m - 5)x^{2m + 3}$$ 在 $$(0, +\infty)$$ 递增,需满足:
.jpg)