.jpg)
正确率80.0%图中的曲线是幂函数$${{y}{=}{{x}^{α}}}$$在第一象限的大致图像，已知$${{α}}$$取$$- 2， ~-\frac{1} {2}， ~ \frac{1} {2}， ~ 2$$四个值，则曲线$$C_{1}， ~ C_{2}， ~ C_{3}， ~ C_{4}$$对应的$${{α}}$$的值依次为（）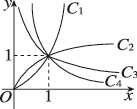
B
A.$$- 2， ~-\frac{1} {2}， ~ \frac{1} {2}， ~ 2$$
B.$$2. ~ \frac{1} {2}， ~-\frac{1} {2}， ~-2$$
C.$$- \frac1 2， ~-2， 2， ~ \frac1 2$$
D.$$2， ~ \frac{1} {2}， ~-2， ~-\frac{1} {2}$$
2、['函数的最大(小)值'， '五个常见幂函数的图象与性质'， '幂函数的定义'， '二次函数的图象分析与判断']正确率40.0%若幂函数$$y=f ( x )$$的图象过点$$( 8， 2 \sqrt{2} )$$，则函数$$f \left( x-1 \right)-f^{2} \left( x \right)$$的最大值为（）
C
A.$$\frac{1} {2}$$
B.$$- \frac{1} {2}$$
C.$$- \frac{3} {4}$$
D.$${{−}{1}}$$
3、['五个常见幂函数的图象与性质'， '不等式比较大小'， '不等式的性质']正确率60.0%已知$$a_{\i} \， \， b \in R$$且$${{a}{>}{b}}$$，则下列不等关系正确的是（）
D
A.$${{a}^{2}{>}{{b}^{2}}}$$
B.$$| a | < | b |$$
C.$$\frac{a} {b} > 1$$
D.$${{a}^{3}{>}{{b}^{3}}}$$
4、['五个常见幂函数的图象与性质'， '不等式的性质']正确率60.0%设函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=x^{-2}$$，若$$f ~ \! \left( \begin{matrix} {a} \\ \end{matrix} \right) ~ < f ~ \! \left( \begin{matrix} {b} \\ \end{matrix} \right)$$，则（）
A
A.$${{a}^{2}{>}{{b}^{2}}}$$
B.$${{a}^{2}{<}{{b}^{2}}}$$
C.$${{a}{<}{b}}$$
D.$${{a}{>}{b}}$$
5、['指数（型）函数的单调性'， '对数（型）函数的单调性'， '单调性的定义与证明'， '五个常见幂函数的图象与性质'， '函数单调性的判断'， '二次函数的图象分析与判断']正确率60.0%下列函数$${{f}{（}{x}{）}}$$中，满足$${{“}}$$对任意的$$x_{1}， ~ x_{2} \in~ ( 0， ~+\infty)$$，当$${{x}_{1}{<}{{x}_{2}}}$$时，都有$$f \ ( \textbf{x}_{1} ) \ < f \ ( \textbf{x}_{2} ) \^{\prime\prime}$$的是（）
C
A.$$f ( x )=\frac{1} {x}$$
B.$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=x^{2}-4 x+4$$
C.$$f \left( \begin{matrix} {x} \\ {x} \\ \end{matrix} \right)=2^{x}$$
D.$$f ( x )=l o g_{\frac1 2} \， x$$
6、['交集'， '描述法'， '五个常见幂函数的图象与性质'， '列举法']正确率60.0%设集合$$A=\{x | x=2 n， \， \， \， n \in N^{*} \}， \， \， \， B=\left\{x \left| x^{\frac{1} {2}} < 2 \right. \right\}$$，则
）
B
A.$${{\{}{2}{\}}}$$
B.$$\{2， ~ 4 \}$$
C.$$\{2， ~ 3， ~ 4 \}$$
D.$$\{1， ~ 2， ~ 3， ~ 4 \}$$
7、['指数（型）函数的单调性'， '五个常见幂函数的图象与性质'， '利用函数单调性比较大小']正确率60.0%已知$${{a}{=}{{0}{.}{2}^{3}}}$$，$${{b}{=}{{0}{.}{3}^{2}}}$$，$${{c}{=}{{0}{.}{3}^{3}}}$$，则$${{a}}$$，$${{b}}$$，$${{c}}$$的大小关系是（）
A
A.$$a < c < b$$
B.$$b < a < c$$
C.$$c < a < b$$
D.$$a < b < c$$
8、['指数（型）函数的单调性'， '五个常见幂函数的图象与性质'， '利用函数单调性比较大小']正确率60.0%已知$$a=e^{3}， ~ b=3^{\pi}， ~ c=e^{\pi}$$，则它们的大小关系是$${{(}{)}}$$
D
A.$$a > b > c$$
B.$$c > b > a$$
C.$$c > a > b$$
D.$$b > c > a$$
9、['五个常见幂函数的图象与性质']正确率80.0%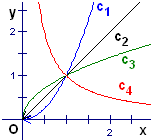
如图所示，曲线是幂函数$${{y}{=}{{x}^{k}}}$$
C
A.$$\mathit{C 1}， \mathit{C 2}， \mathit{C 3}， \mathit{C 4}$$
B.$$\quad C 3， \quad C 2， \quad C 1， \quad C 4$$
C.$$\quad C 4， \quad C 2， \ C 1， \ C 3$$
D.$$\mathit{C 2}， \mathit{C 1}， \mathit{C 3}， \mathit{C 4}$$
10、['对数（型）函数的单调性'， '五个常见幂函数的图象与性质'， '利用函数单调性比较大小']正确率60.0%$${{1}{0}}$$.设$$a=0. 6^{\frac{1} {2}} \，， \， \， \， b=0. 5^{\frac{1} {4}} \，， \， \， \， c=\operatorname{l g} 0. 4$$，则$${{(}{)}}$$
D
A.$$a < b < c$$
B.$$a < c < b$$
C.$$c < b < a$$
D.$$c < a < b$$
1. 解析：根据幂函数$$y = x^α$$的性质，当$$α > 0$$时，函数在第一象限单调递增；当$$α < 0$$时，函数单调递减。且$$α$$的绝对值越大，曲线变化越陡峭。观察图像：
- $$C_1$$增长最快，对应$$α = 2$$
- $$C_2$$增长较缓，对应$$α = \frac{1}{2}$$
- $$C_3$$下降较缓，对应$$α = -\frac{1}{2}$$
- $$C_4$$下降最快，对应$$α = -2$$
正确答案：$$B$$
2. 解析：设幂函数为$$f(x) = x^α$$，代入点$$(8, 2\sqrt{2})$$得：
$$8^α = 2\sqrt{2} \Rightarrow 2^{3α} = 2^{3/2} \Rightarrow α = \frac{1}{2}$$
故$$f(x) = \sqrt{x}$$，所求函数为：
$$g(x) = \sqrt{x-1} - (\sqrt{x})^2 = \sqrt{x-1} - x$$
定义域$$x \geq 1$$，求导得极值点$$x = \frac{5}{4}$$，代入得最大值$$-\frac{3}{4}$$。
正确答案：$$C$$
3. 解析：立方函数$$f(x) = x^3$$在$$R$$上单调递增，故$$a > b \Rightarrow a^3 > b^3$$。
其他选项反例：
- A：$$a = 1, b = -2$$
- B：$$a = 1, b = -2$$
- C：$$a = -1, b = -2$$
正确答案：$$D$$
4. 解析：函数$$f(x) = x^{-2}$$在$$(0, +\infty)$$单调递减，故$$f(a) < f(b) \Rightarrow a > b > 0$$或$$a < b < 0$$。
综合得$$a^2 > b^2$$。
正确答案：$$A$$
5. 解析：题目要求函数在$$(0, +\infty)$$单调递增：
- A：单调递减
- B：二次函数非单调
- C：指数函数单调递增
- D：对数函数单调递减
正确答案：$$C$$
6. 解析：集合$$A = \{2, 4, 6, ...\}$$，集合$$B$$满足$$\sqrt{x} < 2 \Rightarrow x < 4$$。
$$A \cap B = \{2\}$$。
正确答案：$$A$$
7. 解析：计算各值：
- $$a = 0.2^3 = 0.008$$
- $$b = 0.3^2 = 0.09$$
- $$c = 0.3^3 = 0.027$$
故$$a < c < b$$。
正确答案：$$A$$
8. 解析：取自然对数比较：
- $$\ln a = 3$$
- $$\ln b = π \ln 3 ≈ 3.432$$
- $$\ln c = π ≈ 3.142$$
故$$b > c > a$$。
正确答案：$$D$$
9. 解析：同第1题分析，曲线按$$k$$值从大到小依次为$$C_4, C_2, C_1, C_3$$。
正确答案：$$C$$
10. 解析：比较各值：
- $$a = 0.6^{1/2} ≈ 0.7746$$
- $$b = 0.5^{1/4} ≈ 0.8409$$
- $$c = \lg 0.4 ≈ -0.3979$$
故$$c < a < b$$。
正确答案：$$D$$