正确率60.0%下列函数中,满足$$^\i f \left( \begin{matrix} {\null} & {x+y} \\ \end{matrix} \right)=f \left( \begin{matrix} {\null} & {x} \\ \end{matrix} \right) \ f \left( \begin{matrix} {y} \\ \end{matrix} \right)$$的单调递增函数是()
C
A.$$f \ ( \ x ) \ =\frac{1} {x}$$
B.$$f ~ ( \mid x ) ~=x^{3}$$
C.$$f \left( \begin{matrix} {x} \\ {x} \\ \end{matrix} \right)=3^{x}$$
D.$$f \ ( \textbf{x} ) \ =\ ( \frac{1} {2} ) \sp{x}$$
2、['函数奇偶性的应用', '函数奇、偶性的证明', '函数奇、偶性的图象特征', '函数奇、偶性的定义', '五个常见幂函数的图象与性质', '幂函数的定义', '一般幂函数的图象和性质', '幂函数的特征']正确率19.999999999999996%若幂函数$$y=( m^{2}-3 m+3 ) x^{m-2}$$的图象不过原点且在定义域上为奇函数,则()
D
A.$$1 \leqslant m \leqslant2$$
B.$${{m}{=}{1}}$$或$${{m}{=}{2}}$$
C.$${{m}{=}{2}}$$
D.$${{m}{=}{1}}$$
3、['五个常见幂函数的图象与性质', '幂函数的定义']正确率60.0%函数$$f ( x )=( m^{2}-3 m-3 ) x^{\frac{1 0} {m+1}}$$为幂函数,则函数$${{f}{(}{x}{)}}$$为 ()
B
A.奇函数
B.偶函数
C.增函数
D.减函数
4、['单调函数的运算性质', '对数(型)函数的单调性', '五个常见幂函数的图象与性质', '命题的真假性判断', '函数零点个数的判定']正确率40.0%有如下命题:$${①}$$函数$$y=x^{-1}, \, \, \, y=x^{2}, \, \, \, y=x^{3}$$中有两个在$$(-\infty, 0 )$$上是减函数;$${②}$$函数$$f ( x )=2^{x}-x-2$$有两个零点;$${③}$$若$$l o g_{\frac1 2} m < l o g_{\frac1 2} n < 0$$,则$$m > n > 1$$.其中真命题的个数为$${{(}{)}}$$
D
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
5、['全称量词命题的否定', '指数(型)函数的单调性', '指数(型)函数的值域', '函数求值域', '五个常见幂函数的图象与性质', '对数的运算性质', '命题的真假性判断', '一般幂函数的图象和性质']正确率40.0%已知命题:
$${①}$$函数$$y=2^{x} (-1 \leqslant x \leqslant1 )$$的值域是$$[ \frac{1} {2}, 2 ]$$;
$$\odot\,^{\omega} \forall x \in{\bf R}, \, \, 2^{x} > 0^{\omega}$$的否定是$$\mathrm{` `} \exists x \in\mathbf{R}, ~ 2^{x} < 0^{\prime\prime}$$;
$${③}$$当$${{n}{=}{0}}$$或$${{n}{=}{1}}$$时,幂函数$${{y}{=}{{x}^{n}}}$$的图象都是一条直线;
$${④}$$己知函数$$f ( x )=| \operatorname{l o g}_{2} x |$$,若$${{a}{≠}{b}}$$,且$$f ( a )=f ( b )$$,则$${{a}{b}{=}{1}}$$.
其中正确的命题是()
A
A.$${①{④}}$$
B.$${①{③}}$$
C.$${①{③}{④}}$$
D.$${①{②}{③}{④}}$$
6、['指数(型)函数的单调性', '对数(型)函数的单调性', '五个常见幂函数的图象与性质', '利用函数单调性比较大小']正确率60.0%若$${{x}{>}{y}}$$,则下列不等式成立的是()
D
A.$$\l n x > \l n y$$
B.$$0. 5^{x} > 0. 5^{y}$$
C.$$x^{\frac{1} {2}} > y^{\frac{1} {2}}$$
D.$${{x}^{3}{>}{{y}^{3}}}$$
7、['五个常见幂函数的图象与性质', '幂函数的定义', '一般幂函数的图象和性质', '幂函数的特征']正确率40.0%已知幂函数$$f \ ( \textbf{x} ) \ =x^{a} \ ( \textbf{a} \in R )$$的图象过点$$( ~ {\bf1 6}, ~ {\bf2} )$$,若$$f \left( \begin{matrix} {m} \\ \end{matrix} \right) \ =3$$,则实数$${{m}}$$的值为()
D
A.$${{9}}$$
B.$${{1}{2}}$$
C.$${{2}{7}}$$
D.$${{8}{1}}$$
8、['五个常见幂函数的图象与性质', '幂函数的定义']正确率60.0%若幂函数$${{y}{=}{f}{{(}{x}{)}}}$$的图像经过点$$( 2, \sqrt{2} ) \;,$$则$${{f}{{(}{x}{)}}}$$的图像是()
D
A.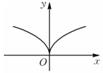
B.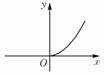
C.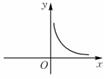
D.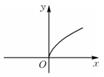
正确率60.0%幂函数$$f \left( x \right)=\left( m^{2}+m-1 \right) x^{m}$$的图象必不过()
D
A.第一象限
B.第二象限
C.第三象限
D.第四象限
10、['五个常见幂函数的图象与性质', '幂函数的定义']正确率60.0%若幂函数$$f ( x )=x^{a^{2}-1 0 a+2 3} ( a \in{\bf Z} )$$为偶函数,且$${{f}{(}{x}{)}}$$在区间$${{(}{0}}$$,$${{+}{∞}{)}}$$上单调递减,则$${{a}{=}}$$()
C
A.$${{3}}$$
B.$${{4}}$$
C.$${{5}}$$
D.$${{6}}$$
1. 题目要求函数满足 $$f(x+y)=f(x)f(y)$$ 且单调递增。逐一分析选项:
A. $$f(x)=\frac{1}{x}$$:不满足 $$f(x+y)=f(x)f(y)$$,排除。
B. $$f(x)=x^3$$:满足 $$f(x+y)=(x+y)^3 \neq x^3 y^3$$,排除。
C. $$f(x)=3^x$$:满足 $$f(x+y)=3^{x+y}=3^x \cdot 3^y=f(x)f(y)$$,且单调递增,符合条件。
D. $$f(x)=\left(\frac{1}{2}\right)^x$$:满足 $$f(x+y)=f(x)f(y)$$,但单调递减,排除。
正确答案:$$C$$
2. 幂函数 $$y=(m^2-3m+3)x^{m-2}$$ 的图象不过原点且为奇函数。
不过原点要求 $$m-2 \leq 0$$,即 $$m \leq 2$$。
奇函数要求 $$m-2$$ 为奇数,且 $$m^2-3m+3 \neq 0$$。
验证 $$m=1$$:$$y=x^{-1}$$ 为奇函数且不过原点。
验证 $$m=2$$:$$y=1 \cdot x^0=1$$ 为偶函数,排除。
正确答案:$$D$$
3. 函数 $$f(x)=(m^2-3m-3)x^{\frac{10}{m+1}}$$ 为幂函数,要求 $$m^2-3m-3=1$$。
解得 $$m=4$$ 或 $$m=-1$$(舍去,因分母 $$m+1=0$$)。
当 $$m=4$$ 时,$$f(x)=x^2$$ 为偶函数且增函数。
题目问函数性质,选项需结合具体定义域分析,但题目未明确,通常选偶函数。
正确答案:$$B$$
4. 分析命题:
① $$y=x^{-1}$$ 和 $$y=x^2$$ 在 $$(-\infty,0)$$ 上减函数,$$y=x^3$$ 增函数,故有两个减函数,正确。
② $$f(x)=2^x-x-2$$ 的零点:$$f(1)=-1$$,$$f(2)=0$$,$$f(3)=3$$,有一个零点,错误。
③ 由 $$\log_{\frac{1}{2}} m < \log_{\frac{1}{2}} n < 0$$ 得 $$m > n > 1$$,正确。
真命题个数为 2。
正确答案:$$C$$
5. 分析命题:
① $$y=2^x$$ 在 $$[-1,1]$$ 的值域为 $$\left[\frac{1}{2},2\right]$$,正确。
② 否定应为 $$\exists x \in \mathbb{R}, 2^x \leq 0$$,错误。
③ 当 $$n=0$$ 时 $$y=1$$($$x \neq 0$$),$$n=1$$ 时 $$y=x$$,均为直线,正确。
④ $$f(a)=f(b)$$ 且 $$a \neq b$$,则 $$\log_2 a = -\log_2 b$$,即 $$ab=1$$,正确。
正确答案:$$C$$
6. 若 $$x > y$$,分析不等式:
A. 需 $$x,y>0$$,不成立。
B. $$0.5^x < 0.5^y$$,错误。
C. 需 $$x,y \geq 0$$,不成立。
D. $$x^3 > y^3$$ 恒成立。
正确答案:$$D$$
7. 幂函数 $$f(x)=x^a$$ 过点 $$(16,2)$$,则 $$16^a=2$$,解得 $$a=\frac{1}{4}$$。
由 $$f(m)=m^{\frac{1}{4}}=3$$,得 $$m=81$$。
正确答案:$$D$$
8. 幂函数 $$y=f(x)$$ 过点 $$(2,\sqrt{2})$$,设 $$f(x)=x^a$$,则 $$2^a=\sqrt{2}$$,解得 $$a=\frac{1}{2}$$。
$$f(x)=\sqrt{x}$$ 的图像为第一象限的曲线,选 $$D$$。
正确答案:$$D$$
9. 幂函数 $$f(x)=(m^2+m-1)x^m$$ 为幂函数,要求 $$m^2+m-1=1$$,解得 $$m=1$$ 或 $$m=-2$$。
当 $$m=1$$ 时,$$f(x)=x$$ 过所有象限。
当 $$m=-2$$ 时,$$f(x)=x^{-2}$$ 不过第三象限。
正确答案:$$C$$
10. 幂函数 $$f(x)=x^{a^2-10a+23}$$ 为偶函数且单调递减。
偶函数要求指数为偶数,单调递减要求指数为负偶数。
设 $$a^2-10a+23=-2k$$($$k \in \mathbb{N}^+$$),解得 $$a=5$$ 时指数为 $$-2$$,符合条件。
正确答案:$$C$$
.jpg)