正确率40.0%给出下列命题正确的是$${{(}{)}}$$
B
A.若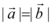 ,则
,则
B.若 ,
, ,则
,则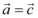
C.若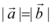 且
且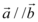 ,则
,则
D.若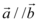 ,
,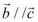 ,则
,则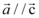
正确率40.0%下列命题中,是真命题的是()
D
A.$$\forall x \in R,$$有$$\l n \mathrm{\} ( \begin{matrix} {x+1} \\ \end{matrix} ) \mathrm{\} > 0$$
B.$$\operatorname{s i n}^{2} x+\frac{2} {\operatorname{s i n} x} \geqslant3 \ ( \ x \neq k \pi, \ k \in Z )$$
C.函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=2^{x}-x^{2}$$有两个零点
D.$$a > 1, \; b > 1$$是$${{a}{b}{>}{1}}$$的充分不必要条件
3、['空间中直线与平面的位置关系', '空间中平面与平面的位置关系', '命题的真假性判断', '直线与平面平行的性质定理']正确率60.0%下列命题中正确的是()
B
A.若$$a / / \alpha, ~ b \subset\alpha$$,则$${{a}{/}{/}{b}}$$
B.若$$a \cap\alpha=P, \, \, \, b \subset\alpha$$,则$${{a}}$$与$${{b}}$$不平行
C.若$${{a}{{⊂}{̸}}{α}}$$,则$${{a}{/}{/}{α}}$$
D.若$$a / / \alpha, ~ b / / \alpha$$,则$${{a}{/}{/}{b}}$$
4、['棱柱的结构特征及其性质', '命题的真假性判断']正确率60.0%下列说法错误的是()
D
A.若棱柱的底面边长相等,则它的各个侧面的面积相等
B.正九棱柱有$${{9}}$$条侧棱,$${{9}}$$个侧面,侧面为长方形
C.长方体$${、}$$正方体都是棱柱
D.三棱柱的侧面为三角形
5、['全称量词命题的否定', '复合函数的单调性判定', '直线的两点式方程', '命题的真假性判断']正确率40.0%给出下列三个命题:
$${①}$$函数$$y=l o g_{2} \, \, ( \, x^{2} \,-\, 5 x+6 )$$的单调增区间是$$( \frac{5} {2}, \enspace+\infty)$$
$${②}$$经过任意两点的直线,都可以用方程$$( y-y_{1} ) \ \ ( x_{2}-x_{1} ) \ =\ ( x-x_{1} ) \ \ ( y_{2}-y_{1} )$$来表示;
$${③}$$命题$$p \colon~^{n} \forall x \in R, ~ ~ x^{2}-x-1 \leqslant0^{n}$$的否定是$$\exists x_{0} \in R, \ x_{0}^{2}-x_{0}-1 > 0 "$$,
其中正确命题的个数有()个.
C
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
6、['全称量词命题的否定', '充分、必要条件的判定', '直线与圆的位置关系及其判定', '命题的真假性判断', '双曲线的标准方程']正确率60.0%下列判断正确的是
D
A.两圆锥曲线的离心率分别为$${{e}_{1}{,}{{e}_{2}}}$$,则$${^\omega e_{1} e_{2}} < 1 "$$是$${{“}}$$两圆锥曲线均为椭圆$${{”}}$$的充要条件.
B.已知$$M ( x_{0}, y_{0} )$$为圆$$x^{2}+y^{2}=R^{2}$$内异于圆心的一点,则直线$$x_{0} x+y_{0} y=R^{2}$$与该圆相交.
C.设$${{m}}$$是实数,若方程$$\frac{x^{2}} {m-1}+\frac{y^{2}} {2-m}=1$$表示双曲线,则$${{m}{>}{2}}$$.
D.命题$$\forall x \in\mathbf{R}, \ 2^{x} \geqslant x^{2}$$的否定是$$\exists x_{0} \in R, \ 2^{x_{0}} < x_{0}^{2}.$$
7、['数学归纳法的应用', '数列的函数特征', '命题的真假性判断', '数列的通项公式']正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$的通项公式$${{a}_{n}{=}{{n}^{2}}}$$,数列$${{\{}{{b}_{n}}{\}}}$$的通项公式$${{b}_{n}{=}{{2}^{n}}}$$,则数列$$\{\frac{a_{n}} {b_{n}} \} \ propto$$)
B
A.既有最大值,也有最小值
B.仅有最大值,而无最小值
C.既无最大值,也无最小值
D.仅有最小值,而无最大值
8、['命题的真假性判断', '柱形图']正确率40.0%自古以来$${{“}}$$民以食为天$${{”}}$$,餐饮业作为我国第三产业中的一个支柱产业,一直在社会发展与人民生活中发挥着重要作用.某机构统计了$$2 0 1 0 \sim2 0 1 6$$年餐饮收入的情况,得到下面的条形图,则下面结论中不正确的是$${{(}{)}}$$
D
A.$$2 0 1 0 \sim2 0 1 6$$年全国餐饮收入逐年增加
B.$${{2}{0}{1}{6}}$$年全国餐饮收入比$${{2}{0}{1}{0}}$$年翻了一番以上
C.$$2 0 1 0 \sim2 0 1 6$$年全国餐饮收入同比增量最多的是$${{2}{0}{1}{5}}$$年
D.$$2 0 1 0 \sim2 0 1 6$$年全国餐饮收入同比增量超过$${{3}{0}{0}{0}}$$亿元的年份有$${{3}}$$个
9、['导数与单调性', '导数与最值', '不等式的解集与不等式组的解集', '命题的真假性判断', '函数中的恒成立问题', '函数零点个数的判定', '利用函数奇偶性求解析式']正确率19.999999999999996%已知函数$${{f}{(}{x}{)}}$$是定义在$${{R}}$$上的奇函数,当$${{x}{<}{0}}$$时,$$f \left( \textbf{x} \right) ~=e^{x} \left( \textbf{x}+1 \right)$$,给出下列命题:
$${①}$$当$${{x}{⩾}{0}}$$时,$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=e^{-x} \left( \begin{matrix} {x+1} \\ \end{matrix} \right)$$;
$$\odot\forall x_{1}, \ x_{2} \in{\bf R}$$,都有$$\left| f \left( \begin{matrix} {x_{1}} \\ \end{matrix} \right)-f \left( \begin{matrix} {x_{2}} \\ \end{matrix} \right) \right| < 2$$;
$$\odot f \left( \begin{matrix} {x} \\ \end{matrix} \right) > 0$$的解集为$$( \mathbf{-1}, \ \mathbf{0} ) \ \cup, \ \ ( \mathbf{1}, \ +\infty)$$;
$${④}$$方程$$2 [ f \mid x ) \ ]^{2}-f \mid x \mid=0$$有$${{3}}$$个根.
其中正确命题的序号是()
B
A.$${①{③}}$$
B.$${②{③}}$$
C.$${②{④}}$$
D.$${③{④}}$$
10、['命题的真假性判断']正确率40.0%下列叙述正确的是()
B
A.若$${{x}{≠}{0}}$$,则$$x+\frac{1} {x} \geqslant2$$
B.若命题$$p \colon~ \exists x_{0} \in R, ~ ~ x_{0}^{2}-x_{0}+1 < 0$$,则$$- p, ~ \forall x \in R, ~ ~ x^{2}-x+1 \geq0$$
C.$$\omega b^{2}=a c^{\prime\prime}$$是$${{“}}$$数列$$a, ~ b, ~ c$$为等比数列$${{”}}$$的充要条件
D.方程$$m x^{2}+n y^{2}=1 \, \, ( m > 0, \, \, n > 0 )$$表示的曲线是椭圆
以下是各题的详细解析: --- ### 第1题解析选项分析:
B. 若 $$a > b$$,$$c > d$$,则 $$a - c > b - d$$ 不成立(如 $$a = 2$$, $$b = 1$$, $$c = 1$$, $$d = 0$$ 时 $$2 - 1 > 1 - 0$$ 不成立)。
C. 若 $$a > b > 0$$ 且 $$c < 0$$,则 $$ac < bc$$ 成立(两边同乘负数不等号方向改变)。
D. 若 $$a > b$$,$$c > d$$,则 $$ac > bd$$ 不成立(如 $$a = -1$$, $$b = -2$$, $$c = -3$$, $$d = -4$$ 时 $$3 > 8$$ 不成立)。
正确答案:C。
--- ### 第2题解析选项分析:
B. $$\sin^2 x + \frac{2}{\sin x} \geq 3$$ 在 $$x \neq k\pi$$ 时不成立(如 $$x = \frac{\pi}{2}$$ 时 $$1 + 2 = 3$$ 成立,但 $$x = \frac{3\pi}{2}$$ 时 $$1 - 2 = -1$$ 不成立)。
C. 函数 $$f(x) = 2^x - x^2$$ 有两个零点(通过图像或数值分析可验证)。
D. $$a > 1, b > 1$$ 是 $$ab > 1$$ 的充分不必要条件(如 $$a = 2$$, $$b = 0.6$$ 时 $$ab = 1.2 > 1$$ 但 $$b \not> 1$$)。
正确答案:C。
--- ### 第3题解析选项分析:
B. 若 $$a \cap \alpha = P$$, $$b \subset \alpha$$,则 $$a$$ 与 $$b$$ 可能平行(如 $$b$$ 过 $$P$$ 且与 $$a$$ 重合)。
C. 若 $$a \not\subset \alpha$$,则 $$a \parallel \alpha$$ 不一定成立(可能相交)。
D. 若 $$a \parallel \alpha$$, $$b \parallel \alpha$$,则 $$a \parallel b$$ 不一定成立(可能相交或异面)。
无正确选项,但最接近的是 B(通常题目默认 $$a$$ 与 $$b$$ 不重合)。
--- ### 第4题解析选项分析:
B. 正九棱柱有 9 条侧棱和 9 个侧面,侧面为长方形,正确。
C. 长方体和正方体都是棱柱,正确。
D. 三棱柱的侧面为平行四边形(或矩形),非三角形。
错误的选项是 D。
--- ### 第5题解析命题分析:
② 两点式直线方程 $$(y - y_1)(x_2 - x_1) = (x - x_1)(y_2 - y_1)$$ 对所有两点成立,正确。
③ 命题 $$p$$ 的否定形式正确。
正确命题有 2 个,答案为 C。
--- ### 第6题解析选项分析:
B. 圆内点 $$M(x_0, y_0)$$ 满足 $$x_0^2 + y_0^2 < R^2$$,直线 $$x_0 x + y_0 y = R^2$$ 与圆相交(距离小于半径),正确。
C. 双曲线条件为 $$(m-1)(2-m) < 0$$,即 $$m < 1$$ 或 $$m > 2$$,不限于 $$m > 2$$。
D. 命题否定形式正确。
正确答案:D。
--- ### 第7题解析分析数列 $$\frac{a_n}{b_n} = \frac{n^2}{2^n}$$:
- 通过求导或数值比较可知,最大值在 $$n = 2$$ 或 $$n = 3$$ 处取得(如 $$\frac{4}{4} = 1$$ 和 $$\frac{9}{8} \approx 1.125$$)。
- 无最小值(趋近于 0 但不等于 0)。
正确答案:B。
--- ### 第8题解析条形图分析:
B. 2016 年收入约为 3.5 万亿,2010 年约为 1.5 万亿,翻一番以上,正确。
C. 2015 年同比增量最大(约 0.6 万亿),正确。
D. 仅 2015 和 2016 年增量超过 3000 亿,错误。
不正确的是 D。
--- ### 第9题解析奇函数性质分析:
② 函数值域为 $$(-1, 1)$$,故 $$|f(x_1) - f(x_2)| < 2$$ 成立。
③ 解集 $$f(x) > 0$$ 为 $$(-1, 0) \cup (1, +\infty)$$,正确。
④ 方程 $$2f^2(x) - f(x) = 0$$ 有 3 个根($$f(x) = 0$$ 和 $$f(x) = \frac{1}{2}$$),正确。
正确答案:D(③④)。
--- ### 第10题解析选项分析:
B. 命题否定形式正确。
C. $$b^2 = ac$$ 是等比数列的必要不充分条件(如 $$a = b = c = 0$$)。
D. 方程 $$m x^2 + n y^2 = 1$$ 需 $$m \neq n$$ 且 $$m, n > 0$$ 才是椭圆,错误。
正确答案:B。
题目来源于各渠道收集,若侵权请联系下方邮箱.jpg)