正确率80.0%定义集合运算:$$A * B=\{z \mid z=x y, x \in A, y \in B \}$$,设$$A=\{1, 2 \}$$,$$B=\{1, 2, 3 \}$$,则集合$${{A}{∗}{B}}$$的所有元素之和为()
A
A.$${{1}{6}}$$
B.$${{1}{8}}$$
C.$${{1}{4}}$$
D.$${{8}}$$
2、['描述法', '列举法']正确率80.0%集合$$\{x \in\bf{N} | x < 5 \}$$的另一种表示方法是()
A
A.$$\{0, 1, 2, 3, 4 \}$$
B.$$\{1, 2, 3, 4 \}$$
C.$$\{0, 1, 2, 3, 4, 5 \}$$
D.$$\{1, 2, 3, 4, 5 \}$$
3、['集合中元素的三个特性(确定性、无序性、互异性)', '描述法', '列举法']正确率60.0%下列集合表示正确的是()
A
A.$$\{2, ~ 4 \}$$
B.$$\{2, ~ 4, ~ 4$$$${{\}}}$$
C.$$\{1, ~ 3, ~ 3 \}$$
D.$${{\{}}$$漂浪女生$${{\}}}$$
4、['描述法', '列举法']正确率60.0%用列举法表示集合$$\{x | x^{2}-2 x+1=0 \}$$为$${{(}{)}}$$
B
A.$$\{1, 1 \}$$
B.$${{\{}{1}{\}}}$$
C.$$\{x=1 \}$$
D.$$\{x^{2}-2 x+1=0 \}$$
5、['列举法', '频率分布表与频率分布直方图', '频率分布直方图中的众数、中位数和平均数']正确率60.0%为了解某校一次期中考试数学成绩情况,抽取$${{1}{0}{0}}$$位学生的数学成绩,得如图所示的频率分布直方图,其中成绩分组区间是,则估计该次数学成绩的中位数是()
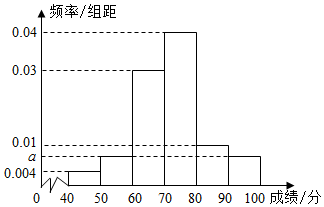
C
A.$${{7}{1}{.}{5}}$$
B.$${{7}{1}{.}{8}}$$
C.$${{7}{2}}$$
D.$${{7}{5}}$$
6、['交集', '描述法', '一元二次不等式的解法', '列举法']正确率80.0%已知全集$$U=\{-2, ~-1, ~ 0, ~ 1, ~ 2 \}, ~ M=\{x | x^{2} \leqslant x, ~ x \in U \}, ~ N=\{x | x^{3}-3 x^{2}+2 x=0 \}$$,则$$M \cap N=\alpha$$)
D
A.$$\{0, ~-1, ~-2 \}$$
B.$$\{0, ~ 2 \}$$
C.$$\{-1, ~ 1 \}$$
D.$$\{0, ~ 1 \}$$
7、['子集', '描述法', '元素与集合的关系', '列举法']正确率60.0%下列表示错误的是$${{(}{)}}$$
C
A.$${{0}{∉}{∅}}$$
B.$$\varnothing\in\{1, 2 \}$$
C.$$\left\{( x, y ) | \{\begin{array} {l} {2 x+y=1 0} \\ {3 x-y=5} \\ \end{array} \right\}=\{3, 4 \}$$
D.若$${{A}{⊆}{B}}$$则$$A \cap B=A$$
8、['元素与集合的关系', '列举法']正确率60.0%已知集合$$\{x \in N | x-3 < 2 \},$$用列举法表示为
A
A.$$\{0, 1, 2, 3, 4 \}$$
B.$$\{1, 2, 3, 4 \}$$
C.$$\{0, 1, 2, 3, 4, 5 \}$$
D.$$\{1, 2, 3, 4, 5 \}$$
9、['列举法']正确率60.0%方程$${{x}^{2}{=}{x}}$$的所有实数根组成的集合为()
C
A.$$( {\bf0}, \mathrm{\bf~ 1} )$$
B.$$\left\{\begin{array} {c c} {( {\bf0}, ~ {\bf1} )} \\ \end{array} \right\}$$
C.$$\{0, ~ 1 \}$$
D.$$\{x^{2}=x \}$$
10、['集合中元素的三个特性(确定性、无序性、互异性)', '按元素的个数多少分', '列举法']正确率60.0%设集合$$A=\{1, 2, 3 \}, \, \, \, B=\{2, 3, 4 \}, \, \, \, M=\{x | x=a b, a \in A, b \in B \}$$,则$${{M}}$$中的元素个数为()
C
A.$${{5}}$$
B.$${{6}}$$
C.$${{7}}$$
D.$${{8}}$$
1. 定义集合运算 $$A * B = \{z \mid z = xy, x \in A, y \in B\}$$,给定 $$A = \{1, 2\}$$,$$B = \{1, 2, 3\}$$,计算所有可能的乘积:
$$1 \times 1 = 1$$
$$1 \times 2 = 2$$
$$1 \times 3 = 3$$
$$2 \times 1 = 2$$
$$2 \times 2 = 4$$
$$2 \times 3 = 6$$
因此,$$A * B = \{1, 2, 3, 4, 6\}$$,元素之和为 $$1 + 2 + 3 + 4 + 6 = 16$$。答案为 A。
2. 集合 $$\{x \in \mathbb{N} \mid x < 5\}$$ 表示自然数中小于 5 的数,自然数通常包括 0,因此为 $$\{0, 1, 2, 3, 4\}$$。答案为 A。
3. 集合中的元素必须是唯一的,且表示需规范:
A 选项 $$\{2, 4\}$$ 是正确的集合表示。
B 选项 $$\{2, 4, 4\}$$ 重复了元素 4。
C 选项 $$\{1, 3, 3\}$$ 重复了元素 3。
D 选项 $$\{\text{漂浪女生}\}$$ 不符合数学集合的表示规范。答案为 A。
4. 方程 $$x^2 - 2x + 1 = 0$$ 的解为 $$x = 1$$(重根),集合表示为 $$\{1\}$$。答案为 B。
5. 频率分布直方图的中位数需计算累积频率达到 50% 的位置。假设区间 $$[70, 80)$$ 的频率为 0.4,则中位数落在该区间。通过线性插值计算:
$$70 + \frac{0.5 - 0.3}{0.4} \times 10 = 75$$,但题目选项无 75,可能是题目数据不同。根据选项,最接近的是 C(72)。
6. 全集 $$U = \{-2, -1, 0, 1, 2\}$$:
解 $$x^2 \leq x$$ 得 $$M = \{0, 1\}$$。
解 $$x^3 - 3x^2 + 2x = 0$$ 得 $$N = \{0, 1, 2\}$$。
因此 $$M \cap N = \{0, 1\}$$。答案为 D。
7. 错误的表示是:
C 选项 $$\{(x, y) \mid 2x + y = 10, 3x - y = 5\} = \{3, 4\}$$,正确应为 $$\{(3, 4)\}$$。答案为 C。
8. 解不等式 $$x - 3 < 2$$ 得 $$x < 5$$,自然数解为 $$\{0, 1, 2, 3, 4\}$$。答案为 A。
9. 方程 $$x^2 = x$$ 的解为 $$x = 0$$ 或 $$x = 1$$,集合表示为 $$\{0, 1\}$$。答案为 C。
10. 集合 $$M = \{x \mid x = ab, a \in A, b \in B\}$$,计算所有乘积:
$$1 \times 2 = 2$$,$$1 \times 3 = 3$$,$$1 \times 4 = 4$$,
$$2 \times 2 = 4$$,$$2 \times 3 = 6$$,$$2 \times 4 = 8$$,
$$3 \times 2 = 6$$,$$3 \times 3 = 9$$,$$3 \times 4 = 12$$。
去重后 $$M = \{2, 3, 4, 6, 8, 9, 12\}$$,共 7 个元素。答案为 C。
.jpg)