.jpg)
正确率60.0%集合$$M=\left\{x \mid y=\sqrt{1-x^{2}} \right\}$$，$$N=\left\{y \mid y=\sqrt{1-x^{2}} \right\}$$，则$${{M}{∩}{{(}{{∁}_{R}}{N}{)}}{=}}$$（）
B
A.$$(-\infty， 0 )$$
B.$$[-1， 0 )$$
C.$$[ 0， 1 ]$$
D.$${{∅}}$$
2、['一元二次方程的解集'， '全集与补集']正确率60.0%已知集合$$U=\{x \in R | x^{2}-2 x=0 \}， \， \， \， M=\{2， \， \， \， 0 \}$$，则$$\mathtt{C}_{U} M=\alpha$$）
C
A.$${{\{}{0}{\}}}$$
B.$${{\{}{2}{\}}}$$
C.$${{∅}}$$
D.$$\{-2， ~ 0， ~ 2 \}$$
3、['全集与补集'， '由集合的关系确定参数'， '绝对值不等式的解法']正确率60.0%设集合$$A=\{x | | x | < 2 \}， \， \， \， B=\{x | x > a \}$$，< 2}，B={x|x >$${{a}{\}}}$$，全集$${{U}{=}{R}}$$.若$${{A}{{⊂}_{−}}{{∁}_{R}}{B}}$$，则$${{(}{)}}$$
B
A.$${{a}{=}{0}}$$
B.$${{a}{⩾}{2}}$$
C.$${{a}{⩽}{2}}$$
D.$${{a}{<}{2}}$$
4、['并集'， '全集与补集'， '集合的混合运算']正确率60.0%已知全集$$U=\{1， ~ 2， ~ 3， ~ 4 \}$$，集合$$A=\{2， \ 3 \}$$，集合$$B=\{1， ~ 3 \}$$，则$$A \cap( {\bf C}_{U} B ) ~=~ ($$）
B
A.$${{\{}{3}{\}}}$$
B.$${{\{}{2}{\}}}$$
C.$$\{2， ~ 3 \}$$
D.$$\{2， ~ 3， ~ 4 \}$$
5、['交集'， '全集与补集']正确率60.0%设全集$$U=\{x \in N | x \leq5 \}$$，集合$$A=\{x \in Z | \frac{6} {3-x} \in N \}， \， \， \， B=\{4， 5 \}$$，则$$A \cap( \complement_{U} B )=($$)
C
A.$${{\{}{1}{\}}}$$
B.$$\{1， 2 \}$$
C.$$\{0， 1， 2 \}$$
D.$$\{1， 2， 3 \}$$
6、['交集'， '全集与补集'， '集合的（真）子集个数问题']正确率60.0%已知全集$$U={\bf Z}， \， A=\{1， 2， 3， 4 \}$$，$$B=\{x \mid( x+1 ) ( x-3 ) > 0， x \in{\bf Z} \}$$，则集合$${{A}{∩}}$$($${{∁}_{U}{B}}$$)的子集个数为（）
C
A.$${{2}}$$
B.$${{4}}$$
C.$${{8}}$$
D.$${{1}{6}}$$
7、['全集与补集']正确率80.0%已知集合$$M=\{x | x^{2}+x-6 \leq0 \}$$，$$N=\{x |-1 < x < 1 \}$$，则$$\mathbf{C}_{M} N=( \mathbf{\Lambda} )$$
C
A.$$[-3， 1 ]$$
B.$$[-1， 2 ]$$
C.$$[-3，-1 ] \cup[ 1， 2 ]$$
D.$${{∅}}$$
8、['全集与补集']正确率80.0%设全集$$U=\{1， 2， 3 \}$$，$$A=\{1， 2 \}$$，则$$\mathbf{C}_{U} A=( \mathbf{\Lambda} )$$
C
A.$${{\{}{1}{\}}}$$
B.$${{\{}{2}{\}}}$$
C.$${{\{}{3}{\}}}$$
D.$$\{1， 3 \}$$
9、['交集'， '全集与补集'， '集合的混合运算']正确率60.0%设集合$${{A}{=}}$$｛$$- 1， 0， 1$$｝$${，{B}{=}}$$$$\{x \in\mathbf{R} | x > 0 \}$$，则$${{A}{∩}{{(}{{∁}_{R}}{B}{)}}{=}}$$（）
A
A.｛$${{−}{1}{，}{0}}$$｝
B.｛$${{−}{1}}$$｝
C.｛$${{1}{，}{0}}$$｝
D.｛$${{1}}$$｝
10、['交集'， 'Venn图'， '全集与补集']正确率40.0%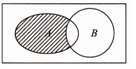
若全集$${{U}{=}{R}}$$，集合$$A=\{0， 1， 2， 3， 4， 5 \}$$，$$B=\{x | x < 3 \}$$，则图中阴影部分表示的集合为$${{(}{)}}$$
C
A.$$\{0， 1， 2， 3 \}$$
B.$$\{0， 1， 2 \}$$
C.$$\{3， 4， 5 \}$$
D.$$\{4， 5 \}$$
1. 解析：首先确定集合$$M$$和$$N$$的范围。
2. 解析：首先求全集$$U$$。
3. 解析：根据题意分析。
4. 解析：求补集和交集。
5. 解析：确定全集和集合$$A$$。
6. 解析：求补集和子集个数。
7. 解析：求补集和差集。
8. 解析：直接求补集。
9. 解析：求补集和交集。
10. 解析：图中阴影部分表示$$A \cap ∁_U B$$。