正确率80.0%已知集合$$M=\{x | x^{2}-3 x \leqslant0 \}$$,$$N=\{x |-2 \leq x \leq2 \}$$,则$$M \cap( \mathbf{C}_{R} N )=( \/ )$$
A.$$\{x | 2 < x \leq3 \}$$
B.$$\{x |-3 \leq x \leq-2 \}$$
C.$$\{x | 0 \leqslant x \leqslant2 \}$$
D.$$\{x |-2 < x \leq3 \}$$
2、['集合间的基本关系', '集合的混合运算']正确率40.0%若$${{x}{∈}{A}}$$,则$$\frac{1} {x} \in A$$,就称$${{A}}$$是和美集合,集合$$M=\left\{-1, 0, \frac{1} {2}, \frac{1} {3}, 1, 3 \right\}$$的所有非空子集中是和美集合的个数为$${{(}{)}}$$
A.$${{4}}$$
B.$${{5}}$$
C.$${{6}}$$
D.$${{7}}$$
3、['集合的混合运算']正确率80.0%设集合$$A=\{1, 2, 6 \}$$,$$B=\{2, 4 \}$$,$$C=\{x \in\mathbf{R} \mid-1 \leqslant x \leqslant5 \}$$,则$$( A \cup B ) \cap C=$$()
B
A.$${{\{}{2}{\}}}$$
B.$${{\{}{1}}$$,$${{2}}$$,$${{4}{\}}}$$
C.$${{\{}{1}}$$,$${{2}}$$,$${{4}}$$,$${{5}{\}}}$$
D.$$\{x \in\mathbf{R} \mid-1 \leq x \leq5 \}$$
4、['集合的混合运算']正确率80.0%设集合$$A=\{x | x > 2 \}$$,$$B=\{x | x^{2}-x-6 > 0 \}$$,则$$A \cup\ss_{R} B=( \textit{} )$$
A
A.$$[-2,+\infty)$$
B.$$( 2,+\infty)$$
C.$$(-\infty,-2 ]$$
D.$$(-\infty, 3 ]$$
5、['指数(型)函数的值域', '集合的混合运算']正确率60.0%已知$$A=\{x |-1 < 2 x-1 < 5 \}, \, \, \, B=\{y | y=2^{x}, \, \, \, x > 0 \}$$,则$$( \C_{R} A ) \cup B=\alpha$$)
A
A.$$\{x | x \leqslant0$$或$${{x}{>}{1}{\}}}$$
B.$$\{x | x \leqslant0$$或$${{x}{⩾}{1}{\}}}$$
C.$$\{x | 1 < x \leq3 \}$$
D.$$\{x | x \geqslant3 \}$$
6、['Venn图', '图示法的应用', '集合的混合运算']正确率60.0%记全集$$U=\{1, 2, 3, 4, 5, 6, 7, 8 \}$$,集合$$A=\{1, 2, 3, 5 \}, B=\{2, 4, 6 \}$$,则图中阴影部分所表示的集合是 ()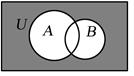
C
A.$$\{4, 6, 7, 8 \}$$
B.$${{\{}{2}{\}}}$$
C.$$\{7, 8 \}$$
D.$$\{1, 2, 3, 4, 5, 6 \}$$
7、['一元二次不等式的解法', '指数方程与指数不等式的解法', '集合的混合运算']正确率60.0%设全集$${{U}{=}{R}}$$,集合$$M=\{x | x^{2} \leqslant x \}, \, \, \, N=\{x | 2^{x} < 1 \}$$,则$$M \cap\complement_{U} N=( \textit{} )$$
A
A.
B.$$( 0, 1 ]$$
C.$$[ 0, 1 )$$
D.$$(-1, 1 ]$$
8、['指数方程与指数不等式的解法', '二次函数的零点及其与对应方程的根、不等式解集之间的关系', '集合的混合运算']正确率60.0%已知全集$${{U}{=}{R}}$$,集合$$M=\{y | y=\sqrt{4-x^{2}}, \, \, \, x \in R \}, \, \, \, N=\{x | 2^{x-1} \geqslant1, \, \, \, x \in R \}$$,则$${{M}{∩}{{(}{{C}_{∪}{N}}{)}}}$$等于()
D
A.$$[-2, ~ 2 ]$$
B.$$[-2, \ 1 )$$
C.$$[ 1, ~ 4 ]$$
D.$$[ 0, \ 1 )$$
9、['子集', '集合的混合运算']正确率60.0%已知集合$$M=\left\{-1, 0, 1, 2, 3 \right\}, N=\left\{-2, 0 \right\}$$,则下列结论正确的是$${{(}{)}}$$
D
A.$${{N}{⊆}{M}}$$
B.$$M \cap N=N$$
C.$$M \cup N=M$$
D.$$M \cap N=\{0 \}$$
10、['集合的混合运算']正确率80.0%已知全集$${{U}{=}{R}}$$,集合$$A=\{0, 1, 2, 3, 4, 5 \}$$,$$B=\{x \in R | x \geqslant3 \}$$,则$$A \cap\complement_{U} B=( \/ )$$
C
A.$$\{4, 5 \}$$
B.$$\{3, 4, 5 \}$$
C.$$\{0, 1, 2 \}$$
D.$$\{0, 1, 2, 3 \}$$
1. 解析:
集合 $$M = \{x | x^2 - 3x \leq 0\}$$ 的解为 $$0 \leq x \leq 3$$。
集合 $$N = \{x | -2 \leq x \leq 2\}$$,其补集 $$\mathbf{C}_R N = \{x | x < -2 \text{ 或 } x > 2\}$$。
$$M \cap \mathbf{C}_R N = \{x | 2 < x \leq 3\}$$,对应选项 A。
2. 解析:
和美集合要求若 $$x \in A$$,则 $$\frac{1}{x} \in A$$。
集合 $$M = \{-1, 0, \frac{1}{2}, \frac{1}{3}, 1, 3\}$$ 的非空子集中满足条件的为:
1. $$\{-1\}$$(因为 $$\frac{1}{-1} = -1 \in \{-1\}$$)
2. $$\{1\}$$(因为 $$\frac{1}{1} = 1 \in \{1\}$$)
3. $$\{3, \frac{1}{3}\}$$(因为 $$\frac{1}{3} \in \{3, \frac{1}{3}\}$$ 且 $$\frac{1}{\frac{1}{3}} = 3 \in \{3, \frac{1}{3}\}$$)
4. $$\{-1, 1\}$$(因为 $$\frac{1}{-1} = -1 \in \{-1, 1\}$$ 且 $$\frac{1}{1} = 1 \in \{-1, 1\}$$)
共有 4 个,对应选项 A。
3. 解析:
$$A \cup B = \{1, 2, 4, 6\}$$。
$$C = \{x | -1 \leq x \leq 5\}$$。
$$(A \cup B) \cap C = \{1, 2, 4\}$$,对应选项 B。
4. 解析:
集合 $$B = \{x | x^2 - x - 6 > 0\} = \{x | x < -2 \text{ 或 } x > 3\}$$。
补集 $$\mathbf{C}_R B = \{x | -2 \leq x \leq 3\}$$。
$$A \cup \mathbf{C}_R B = \{x | x \geq -2\}$$,即 $$[-2, +\infty)$$,对应选项 A。
5. 解析:
$$A = \{x | -1 < 2x - 1 < 5\} = \{x | 0 < x < 3\}$$。
补集 $$\mathbf{C}_R A = \{x | x \leq 0 \text{ 或 } x \geq 3\}$$。
$$B = \{y | y = 2^x, x > 0\} = \{y | y > 1\}$$。
$$(\mathbf{C}_R A) \cup B = \{x | x \leq 0 \text{ 或 } x > 1\}$$,对应选项 A。
6. 解析:
阴影部分表示 $$(A \cup B)$$ 的补集。
$$A \cup B = \{1, 2, 3, 4, 5, 6\}$$。
补集为 $$\{7, 8\}$$,对应选项 C。
7. 解析:
$$M = \{x | x^2 \leq x\} = \{x | 0 \leq x \leq 1\}$$。
$$N = \{x | 2^x < 1\} = \{x | x < 0\}$$。
补集 $$\complement_U N = \{x | x \geq 0\}$$。
$$M \cap \complement_U N = [0, 1]$$,对应选项 A。
8. 解析:
$$M = \{y | y = \sqrt{4 - x^2}\} = [0, 2]$$。
$$N = \{x | 2^{x-1} \geq 1\} = \{x | x \geq 1\}$$。
补集 $$\mathbf{C}_U N = \{x | x < 1\}$$。
$$M \cap \mathbf{C}_U N = [0, 1)$$,对应选项 D。
9. 解析:
$$M = \{-1, 0, 1, 2, 3\}$$,$$N = \{-2, 0\}$$。
$$M \cap N = \{0\}$$,对应选项 D。
10. 解析:
$$B = \{x | x \geq 3\}$$,补集 $$\complement_U B = \{x | x < 3\}$$。
$$A \cap \complement_U B = \{0, 1, 2\}$$,对应选项 C。
.jpg)