正确率40.0%已知集合$$M=\{x \in\mathbf{N}^{*} | 1 \leqslant x \leqslant1 5 \}$$,集合$$A_{1} \,, \, \, A_{2} \,, \, \, A_{3}$$满足:
①每个集合中都恰有$${{5}}$$个元素;
②$$A_{1} \cup A_{2} \cup A_{3}=M$$.
若集合$${{A}_{i}}$$中元素的最大值与最小值之和称为集合$${{A}_{i}}$$的特征数,记为$$X_{i} ( i=1, ~ 2, ~ 3 ),$$则$$X_{1}+X_{2}+X_{3}$$的值不可能为()
A
A.$${{3}{7}}$$
B.$${{3}{9}}$$
C.$${{4}{8}}$$
D.$${{5}{7}}$$
2、['集合的新定义问题', '集合的(真)子集个数问题', '等差数列的基本量']正确率19.999999999999996%以区间$$( 0, m )$$内的整数$${{(}{m}{>}{1}}$$,且$${{m}{∈}{N}{)}}$$为分子,以$${{m}}$$为分母的分数组成集合$${{A}_{1}}$$,其所有元素之和为$${{a}_{1}}$$;以区间$$( 0, m^{2} )$$内的整数$${{(}{m}{>}{1}}$$,且$${{m}{∈}{N}{)}}$$为分子,以$${{m}^{2}}$$为分母组成不属于$${{A}_{1}}$$的分数集合$${{A}_{2}}$$,其所有元素之和为$${{a}_{2}{…}{…}}$$以此类推,以区间$$( 0, m^{n} )$$内的整数$${{(}{m}{>}{1}}$$,且$${{m}{∈}{N}{)}}$$为分子,以$${{m}^{n}}$$为分母组成不属于集合$$A_{1} \dots A_{2} \dots, ~ A_{n-1}$$的分数集合$${{A}_{n}}$$,其所有元素之和为$${{a}_{n}}$$,则$$a_{1}+a_{2}+a_{3}+\ldots+a_{n}=$$()
B
A.$$\frac{m^{n}+1} {2}$$
B.$$\frac{m^{n}-1} {2}$$
C.$$\frac{m^{n}} {2}$$
D.$$\frac{n} {2}$$
3、['集合的新定义问题', '集合的混合运算']正确率60.0%设$${{M}{,}{P}}$$设两个非空集合,定义$${{M}}$$与$${{P}}$$的差集为$$M-P=\{x | x \in M$$且$${{x}{∉}{P}{\}}}$$,则$$M-( M-P )$$等于()
B
A.$${{P}}$$
B.$${{M}{⋂}{P}}$$
C.$${{M}{⋃}{P}}$$
D.$${{M}}$$
4、['集合的新定义问题']正确率60.0%定义$$A-B=\{x | x \in A \}$$且$${{x}{∉}{B}{\}}}$$,若$$A=\{1, 2, 3, 4, 5 \}, \, \, \, B=\{2, 3, 6 \}$$,则$$A-( A-B )$$等于()
B
A.$$\{2, 3, 6 \}$$
B.$$\{2, 3 \}$$
C.$$\{1, 4, 5 \}$$
D.$${{\{}{6}{\}}}$$
5、['集合的新定义问题', '两点间的距离']正确率40.0%对于平面上点$${{P}}$$和曲线$${{C}}$$,任取$${{C}}$$上一点$${{Q}}$$,若线段$${{P}{Q}}$$的长度存在最小值,则称该值为点$${{P}}$$到曲线$${{C}}$$的距离,记作$$\textbf{d} ( P, \ C )$$若曲线$${{C}}$$是边长为$${{6}}$$的等边三角形,则点集$$D=\{P | d ~ ( ~ P, ~ C ) ~ \leq1 \}$$所表示的图形的面积为()
D
A.$${{3}{6}}$$
B.$$3 6-3 \sqrt{3}$$
C.$${{3}{6}{+}{π}}$$
D.$$3 6-3 \sqrt{3}+\pi$$
6、['集合的新定义问题']正确率40.0%设$${{A}{,}{B}}$$是非空集合,定义:$$A \times B=\{x | x \in A \cup B$$且$$x \notin A \cap B \}$$,已知$$A=\{x | y=\sqrt{2 x-x^{2}} \}, \, \, \, B=\{x | x > 1 \}$$,则$${{A}{×}{B}}$$等于()
A
A.$$[ 0, ~ 1 ] \cup~ ( \mathrm{\bf~ 2}, ~+\infty)$$
B.$$[ 0, \ 1 ) \cup\ ( \mathbf{2}, \mathbf{+}$$
C.$$[ 0, \ 1 ]$$
D.$$[ 0, \ 2 )$$
7、['集合的新定义问题']正确率40.0%设$${{P}{,}{Q}}$$是两个非空集合,定义集合间的一种运算$${\mathrm{` `}} \otimes{\mathrm{''}} \colon{P} \otimes{Q}=\{x | x \in{P} \cup{Q} \}$$且$$x \notin P \cap Q \}$$.如果$$P=\{x | 0 \leqslant x \le2 \}, \, \, \, Q=\{x | x > 1 \}$$,则$$P \otimes Q=\langle$$)
B
A.$$[ 0, \ 1 ) \cup\ ( \mathbf{2}, \mathbf{+}$$
B.$$[ 0, ~ 1 ] \cup~ ( \mathrm{\bf~ 2}, ~+\infty)$$
C.$$[ 1, \ 2 ]$$
D.$$( \mathrm{\bf~ 2, ~}+\infty)$$
8、['集合的新定义问题', '区间']正确率40.0%已知区间$$A=[ m-\frac{1} {3}, \ m ]$$和$$B=[ n, ~ n+\frac{3} {4} ]$$均为$$[ 0, \ 1 ]$$的子区间,定义$${{b}{−}{a}}$$为区间$$[ a, ~ b ]$$的长度,则当$${{A}{∩}{B}}$$的长度达到最小时$${{m}{n}}$$的值为()
C
A.$${{0}}$$
B.$$\frac1 {1 2}$$
C.$${{0}}$$或$$\frac1 {1 2}$$
D.$${{0}}$$或$${{1}}$$
9、['集合的新定义问题', '集合间关系的判断']正确率60.0%在集合$$\left\{a, b, c, d \right\}$$上定义两种运算$${{⊕}}$$和$${{⊗}}$$如图,那么$$d \otimes( a \oplus c )=($$)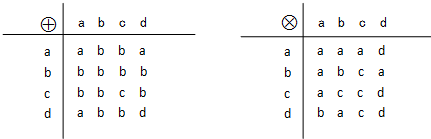
A
A.$${{a}}$$
B.$${{b}}$$
C.$${{c}}$$
D.$${{d}}$$
10、['交集', '并集', '集合的新定义问题']正确率40.0%定义运算$$A * B=\{( x, y ) | x \in A \cap B, y \in A \cup B \}$$,若集合$$A=\left\{-1, 0, 1 \right\}, B=\left\{0, 1, 2, 3 \right\}$$,则$${{A}{∗}{B}}$$中元素的个数为()
B
A.$${{7}}$$
B.$${{1}{0}}$$
C.$${{3}{2}}$$
D.$${{2}{5}}$$
1. 解析:集合$$M=\{1,2,\dots,15\}$$,分成三个子集$$A_1,A_2,A_3$$,每个子集有5个元素且并集为$$M$$。特征数$$X_i$$为集合$$A_i$$的最大值与最小值之和。我们需要计算$$X_1+X_2+X_3$$的可能取值。
2. 解析:定义集合$$A_n$$为以$$m^n$$为分母且不属于前$$n-1$$个集合的分数之和为$$a_n$$。
3. 解析:定义差集$$M-P=\{x \in M \text{且} x \notin P\}$$,求$$M-(M-P)$$。
4. 解析:定义$$A-B=\{x \in A \text{且} x \notin B\}$$,求$$A-(A-B)$$。
5. 解析:定义点$$P$$到曲线$$C$$的距离为$$d(P,C)$$,求点集$$D=\{P | d(P,C) \leq 1\}$$的面积。
6. 解析:定义$$A \times B=\{x \in A \cup B \text{且} x \notin A \cap B\}$$,即对称差集。
7. 解析:定义$$P \otimes Q=\{x \in P \cup Q \text{且} x \notin P \cap Q\}$$。
8. 解析:区间$$A=[m-\frac{1}{3},m]$$和$$B=[n,n+\frac{3}{4}]$$均为$$[0,1]$$的子区间,求$$A \cap B$$长度最小时的$$mn$$。
9. 解析:根据运算表,求$$d \otimes (a \oplus c)$$。
10. 解析:定义$$A * B=\{(x,y) | x \in A \cap B, y \in A \cup B\}$$,求元素个数。
.jpg)